ResNet总结
Posted caiyi-xu
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了ResNet总结相关的知识,希望对你有一定的参考价值。
1 ResNet
1.1 Why
当模型层数增加到某种程度,模型的效果将会不升反降,发生退化。
不是过拟合:训练误差也大
不是梯度消失/爆炸:BN基本解决了这个问题
问题:堆加新的层后,这些层很难做到恒等映射,由于非线性激活。
1.2 解读
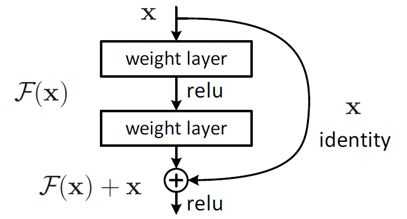
把网络设计为H(x) = F(x) + x,即直接把恒等映射作为网络的一部分。就可以把问题转化为学习一个残差函数F(x) = H(x) - x. 只要F(x)=0,就构成了一个恒等映射H(x) = x。 而且,拟合残差至少比拟合恒等映射容易得多。
用数学语言描述,假设Residual Block的输入为 ,则输出
等于:
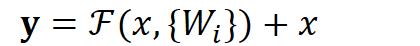
其中 是我们学习的目标,即输出输入的残差
。以上图为例,残差部分是中间有一个Relu激活的双层权重,即:
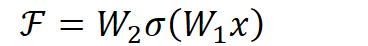
其中 指代Relu,而
指代两层权重。
顺带一提,这里一个Block中必须至少含有两个层,否则就会出现很滑稽的情况:
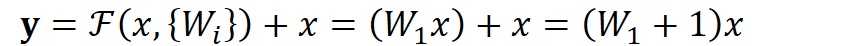
显然这样加了和没加差不多……
1.3 结构
结构参考
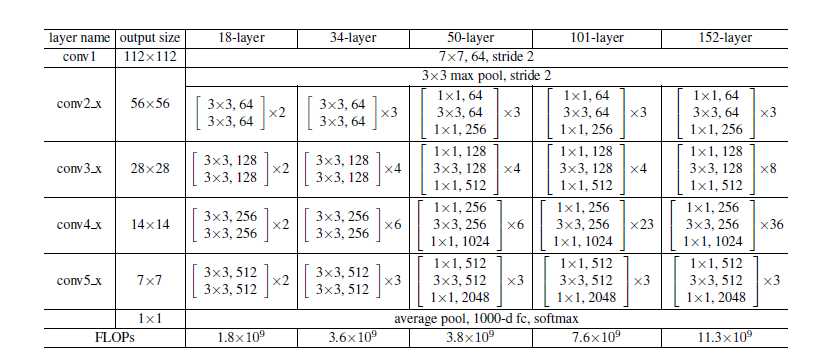
ResNet是仿照VGG-19,只不过改变具体最小单元。
1.3.1 可能最小结构
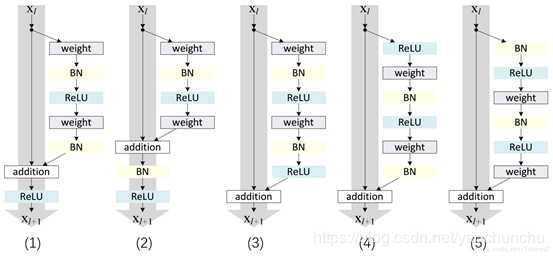
1 是原文中采用, 5 是改进版
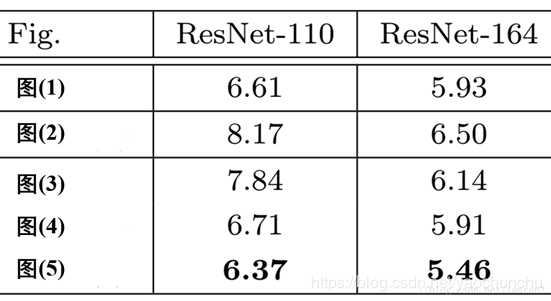
1.3.2 维度不同问题
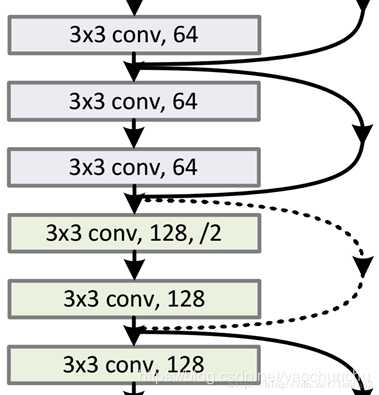
维度不一致体现在两个层面:
- 空间上不一致
- 深度上不一致
空间上不一致很简单,只需要在跳接的部分给输入x加上一个线性映射 ,即:
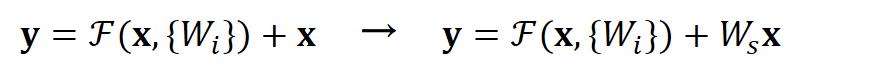
而对于深度上的不一致,则有两种解决办法,一种是在跳接过程中加一个1*1的卷积层进行升维,另一种则是直接简单粗暴地补零。事实证明两种方法都行得通。
1.3.3 实际18/34/50/101/152细节
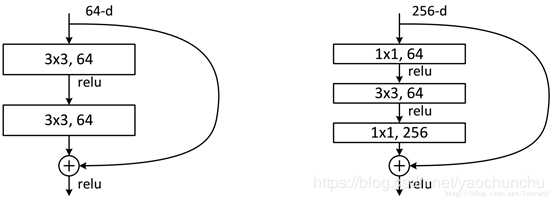
这两种结构分别针对ResNet34(左图)和ResNet50/101/152(右图),一般称整个结构为一个”building block“。其中右图又称为”bottleneck design”,目的一目了然,就是为了降低参数的数目。看右图,输入是一个3×3×256的特征,第一个步骤用64个1x1的卷积把256维channel降到64维,然后在最后通过1x1卷积恢复到256个channel,整体上用的参数数目:1x1x256x64 + 3x3x64x64 + 1x1x64x256 = 69632,而不使用bottleneck的话参考左图,输入假设是3x3x256,第一步经过256个卷积核3×3×256,第二部再经过256个卷积核3×3×256。所以参数数目: 3x3x256x256x2 = 1179648,差了16.94倍。
1.4 代码解读
总体结构
def inference(hypes, images, train=True,
num_classes=1000,
num_blocks=[3, 4, 6, 3], # defaults to 50-layer network
preprocess=True,
bottleneck=True):
# if preprocess is True, input should be RGB [0,1], otherwise BGR with mean
# subtracted
layers = hypes[‘arch‘][‘layers‘]
if layers == 50:
num_blocks = [3, 4, 6, 3]
elif layers == 101:
num_blocks = [3, 4, 23, 3]
elif layers == 152:
num_blocks = [3, 8, 36, 3]
else:
assert()
# 减均值,调顺序
if preprocess:
x = _imagenet_preprocess(images)
is_training = tf.convert_to_tensor(train,
dtype=‘bool‘,
name=‘is_training‘)
logits = {}
with tf.variable_scope(‘scale1‘):
x = _conv(x, 64, ksize=7, stride=2)
x = _bn(x, is_training, hypes)
x = _relu(x)
scale1 = x
with tf.variable_scope(‘scale2‘):
x = _max_pool(x, ksize=3, stride=2)
x = stack(x, num_blocks[0], 64, bottleneck, is_training, stride=1,
hypes=hypes)
scale2 = x
with tf.variable_scope(‘scale3‘):
x = stack(x, num_blocks[1], 128, bottleneck, is_training, stride=2,
hypes=hypes)
scale3 = x
with tf.variable_scope(‘scale4‘):
x = stack(x, num_blocks[2], 256, bottleneck, is_training, stride=2,
hypes=hypes)
scale4 = x
with tf.variable_scope(‘scale5‘):
x = stack(x, num_blocks[3], 512, bottleneck, is_training, stride=2,
hypes=hypes)
scale5 = x
logits[‘deep_feat‘] = scale5
logits[‘early_feat‘] = scale3
if train:
restore = tf.global_variables()
hypes[‘init_function‘] = _initalize_variables
hypes[‘restore‘] = restore
return logits每一个尺度scale下
def stack(x, num_blocks, filters_internal, bottleneck, is_training, stride,
hypes):
for n in range(num_blocks):
s = stride if n == 0 else 1
with tf.variable_scope(‘block%d‘ % (n + 1)):
x = block(x,
filters_internal,
bottleneck=bottleneck,
is_training=is_training,
stride=s,
hypes=hypes)
return x具体到每个残差单元
def block(x, filters_internal, is_training, stride, bottleneck, hypes):
filters_in = x.get_shape()[-1]
# Note: filters_out isn‘t how many filters are outputed.
# That is the case when bottleneck=False but when bottleneck is
# True, filters_internal*4 filters are outputted. filters_internal
# is how many filters
# the 3x3 convs output internally.
if bottleneck:
filters_out = 4 * filters_internal
else:
filters_out = filters_internal
shortcut = x # branch 1
if bottleneck:
with tf.variable_scope(‘a‘):
x = _conv(x, filters_internal, ksize=1, stride=stride)
x = _bn(x, is_training, hypes)
x = _relu(x)
with tf.variable_scope(‘b‘):
x = _conv(x, filters_internal, ksize=3, stride=1)
x = _bn(x, is_training, hypes)
x = _relu(x)
with tf.variable_scope(‘c‘):
x = _conv(x, filters_out, ksize=1, stride=1)
x = _bn(x, is_training, hypes)
else:
with tf.variable_scope(‘A‘):
x = _conv(x, filters_internal, ksize=3, stride=stride)
x = _bn(x, is_training, hypes)
x = _relu(x)
with tf.variable_scope(‘B‘):
x = _conv(x, filters_out, ksize=3, stride=1)
x = _bn(x, is_training, hypes)
with tf.variable_scope(‘shortcut‘):
if filters_out != filters_in or stride != 1:
shortcut = _conv(shortcut, filters_out, ksize=1, stride=stride)
shortcut = _bn(shortcut, is_training, hypes)
return _relu(x + shortcut)
2 预处理相关技巧
2.1 去均值
2.1.1 Define
R G B 每通道减去均值 (R_mean,G_mean,B_mean,均值为总样本统计得到的。
2.1.2 Why
从主成分分析(PCA)入手解释
可以移除图像的平均亮度值。很多情况下我们对图像的照度并不感兴趣,而更多地关注其内容,比如在对象识别任务中,图像的整体明亮程度并不会影响图像中存在的是什么物体。
从反向传播计算入手
如果输入层 很大,在反向传播时候传递到输入层的梯度就会变得很大。
如果梯度非常大,学习率就必须非常小(否则会跳过local minimum),因此,学习率(学习率初始值)的选择需要参考输入层的数值,不如直接将数据归一化,这样学习率就不必再根据数据范围作调整。
2.1.2 How
值得一提自然界图像平均RGB为120左右。理论上RGB是统计训练集的,本着测试集与其分开规则。然而由于Imagenet图片海量,可以直接用其统计的RGB。
IMAGENET_MEAN_BGR = [103.062623801, 115.902882574, 123.151630838, ]
def _imagenet_preprocess(rgb):
"""Changes RGB [0,1] valued image to BGR [0,255] with mean subtracted."""
red, green, blue = tf.split(
axis=3, num_or_size_splits=3, value=rgb * 255.0)
bgr = tf.concat(axis=3, values=[blue, green, red])
bgr -= IMAGENET_MEAN_BGR
return bgr3 网络中相关技巧
3.1 Batch Normalization(BN) 批归一化/规范化
Batch Normalization原理与实战
深度学习中 Batch Normalization为什么效果好?
3.1.1 原理,Why
一方面,当底层网络中参数发生微弱变化时,由于每一层中的线性变换与非线性激活映射,这些微弱变化随着网络层数的加深而被放大(类似蝴蝶效应);另一方面,参数的变化导致每一层的输入分布会发生改变,进而上层的网络需要不停地去适应这些分布变化,使得我们的模型训练变得困难。上述这一现象叫做Internal Covariate Shift。
当使用PCA白化时,可以使输入特征分布具有相同的均值与方差(均值为0,方差为1)
但计算成本高,且改变了每一层分布,丢失原始表达能力
BN的改进:
1、单独对每个特征进行normalizaiton就可以了,让每个特征都有均值为0,方差为1的分布。
2、再加个线性变换操作,让这些数据再能够尽可能恢复本身的表达能力。
以上是关于ResNet总结的主要内容,如果未能解决你的问题,请参考以下文章