动态规划--矿工挖矿

Posted 2020-11-26 xiximayou

动态规划三要素：边界、最优子问题、状态转移方程；

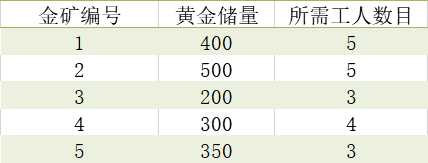
问题描述：现有10个矿工，5个金矿，每个金矿有对应金子和需要开采的人数，问你最多能够获得多少金子？

这是一个典型的动态规划问题，动态规划的核心是如何将问题转换为重叠的子问题，并且写出状态转移方程。

首先我们定义相应的参数：

矿工个数：n=10

金矿个数：w=5

金子数量：g=[400,500,200,300,350]

需要人数：p=[5,5,3,4,4]

p[i]代表挖了第i个金矿所需人数，g[i]代表挖了第 i个金矿得到的金子数。令F(n,w)表示n个人挖w个金矿能够得到的最大金子数。

当n<p[i]时，也就是说挖第i个金矿的人数不够，那么此时可以获得的最大金子数就是挖第i-1个金矿时的金子：

F(n,w)=F(n,w-1)

那么我们当n>p[i]时，有以下方程：

F(n,w)=max(F(n,w-1),F(n-p[i],w-1)+g[i])

 

表示n个人挖w个金矿能够得到的最大金子数=最大值(n个人挖w-1个金矿，((n-p[i])个人挖w-1个金矿)+g[i]))

最终代码：

n=10
w=5
g=[400,500,200,300,350]
p=[5,5,3,4,3]
def goldMining(n,w,g,p):
    #初始化数组，用于存储信息，注意为了更好计算，共有11列，第一列作为辅助位
    dp = [[0 for _ in range(n+1)] for _ in range(w)]
    #边界就是10个人只挖第1个金矿
    #[0, 0, 0, 0, 0, 400, 400, 400, 400, 400, 400]
    for i in range(1,n+1):
        if i<p[0]:
            dp[0][i]=0
        else:
            dp[0][i]=g[0]
    #依次遍历金矿，人数
    for i in range(1,w):
        for j in range(1,n+1):
            #如果当前人数小于挖这座金矿的人数
            if j<p[i]:
                #则当前最大金矿就是挖前一个金矿的相应人数的值
                dp[i][j]=dp[i-1][j]
            else:
                #否则就用如下公式计算
                dp[i][j]=max(dp[i-1][j],dp[i-1][j-p[i]]+g[i])
    return dp

dp=goldMining(n,w,g,p)
for i in range(len(dp)):
    print(dp[i])

最终结果：

 

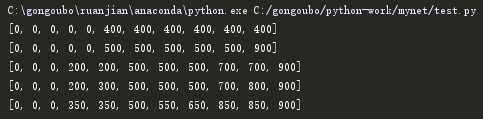
可以看到，我们最终可以获得的最大金子数是900，也就是挖第一个和第二个金矿。