线性分段插值
Posted guliangt
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了线性分段插值相关的知识,希望对你有一定的参考价值。
1.插值函数
%%分段线性插值
function PLI = Piecewise_linear_interpolation(X,f,precision)
[m,n] = size(X);a = min(X);b = max(X);
X = sort(X);
F = subs(f,X);
for k = 1:n-1
B = Basic_fun(X,k);
I = B(1)*F(k)+B(2)*F(k+1);
PLI{1,k} = [X(k),X(k+1)];
PLI{2,k} = I;
t{k} = X(k):(X(k+1)-X(k))/precision:X(k+1);
T{k} = subs(I,t{k});
Y_real{k} = subs(f,t{k});
end
for k = 1:n-1
t_((precision+1)*(k-1)+1:(precision+1)*k) = t{k};
T_((precision+1)*(k-1)+1:(precision+1)*k) = T{k};
Y_real_((precision+1)*(k-1)+1:(precision+1)*k)= Y_real{k};
end
h = figure;
set(h,‘color‘,‘w‘);
plot(X,F,‘r*‘,t_,T_,‘g‘,t_,Y_real_,‘b‘);
xlabel(‘x shaft‘);ylabel(‘y shaft‘);
legend(‘F:节点对应函数值‘,‘T:分段线性插值函数图像‘,‘Y_real:真实函数图像‘);
title(‘分段线性插值‘);
grid on
end
2.基函数
%%基函数,max(X)>k>0 function BF = Basic_fun(X,k) X = sort(X); syms x; BF(1) = (x-X(k+1))/(X(k)-X(k+1)); BF(2) = (x-X(k))/(X(k+1)-X(k)); end
3.拟合值函数
%%线性插值拟合值
function LIV = Linear_interpolation_value(X,f,precision,x_value)
[m,n] = size(X);a = min(X);b = max(X);
X = sort(X);
Answer = Piecewise_linear_interpolation(X,f,precision);
for i = 1:n-1
if x_value >= X(i) && x_value <= X(i+1)
s = i;
end
end
LIV{1,1} = ‘线性插值拟合值‘;
LIV{2,1} = vpa(subs(Answer{2,s},x_value),6);
LIV{1,2} = ‘真实值‘;
LIV{2,2} = vpa(subs(f,x_value),6);
LIV{1,3} = ‘误差‘;
LIV{2,3} = abs(LIV{2,1}-LIV{2,2});
end
4.例子
clear all clc X = -5:1:5; syms x; f = - 0.08858*x^8 + 3.694*x^7 - 64.7*x^6 + 617.8*x^5 - 3490.0*x^4 + 11820.0*x^3 - 23150.0*x^2 + 23580.0*x - 9319.0; precision = 200; %%分段线性插值 disp(‘分段线性插值‘); Piecewise_linear_interpolation(X,f,precision)
结果
分段线性插值
S =
2×10 cell 数组
列 1 至 4
{1×2 double} {1×2 double} {1×2 double} {1×2 double}
{1×1 sym } {1×1 sym } {1×1 sym } {1×1 sym }
列 5 至 8
{1×2 double} {1×2 double} {1×2 double} {1×2 double}
{1×1 sym } {1×1 sym } {1×1 sym } {1×1 sym }
列 9 至 10
{1×2 double} {1×2 double}
{1×1 sym } {1×1 sym }
>> S{2,:}
ans =
(227077586881*x)/50000 + 37695704689/2500
ans =
(3983468847*x)/2000 + 60987657739/12500
ans =
(7723057429*x)/10000 + 30518164433/25000
ans =
(2518396259*x)/10000 + 4494858583/25000
ans =
(3136314129*x)/50000 - 9319
ans =
(465835271*x)/50000 - 9319
ans =
(422501*x)/10000 - 1113617/25000
ans =
4111433/25000 - (622509*x)/10000
ans =
- (271*x)/80 - 151661/12500
ans =
2072089/2500 - (10681481*x)/50000
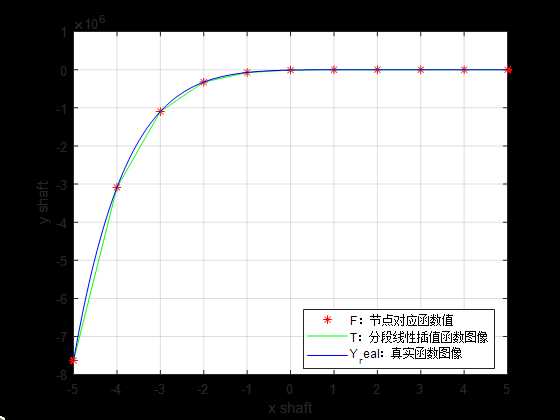
图像如下
以上是关于线性分段插值的主要内容,如果未能解决你的问题,请参考以下文章