算法设计与分析 6.5 汽车维修.md

Posted 2020-11-26 yejifeng

★题目描述

有N位客户的汽车等待维修，现在M个维修员，每个维修员修理每台汽车的时间不同，

请安排每个维修员需要维修的车与维修顺序，使得所有客户总等待时间最少。

★输入格式

输入的第一行两个数字M，N(1<=N，M<=20，1<=K<=20)，表示维修员数目与汽车数目。

接下来N行每行M个数字Ti，j(1<=Ti，j<=20)代表第j个维修员修理第i辆车需要Ti，j时间

★输出格式

输出最小的总等待时间。

★样例输入

2 2
3 2
1 4

★样例输出

3

★提示

无

★参考代码

/*
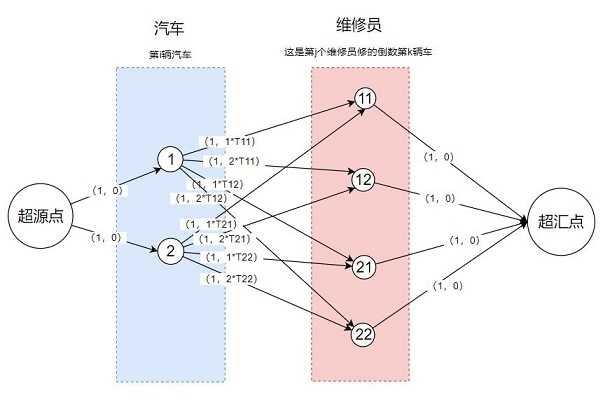
这道题是最小费用网络

现在问题是要如何构建这个网络图

如何表达一辆车对总等待时间的贡献？
第i号车是第j位维修员修理的倒数第k辆车，那么对总时间的贡献 T = k*T[i,j] 
（为了表达简洁，这里用“倒数第k辆车”，这样对结果没有影响）

网络图如上所示

现在就是依据这张图，求最大流量的最小费用 
*/
#include<bits/stdc++.h>
using namespace std;

int M,N;
int T[20+5][20+5]; 
struct Edge{
    int to,next,flow,dis;//flow流量 dis花费 
}E[10000]; //保存的数据是边 
int H[10000], numEdge;
void AddEdge(int u, int v, int f, int d){
    ++numEdge;
    E[numEdge].to=v;
    E[numEdge].flow=f;
    E[numEdge].dis=d;
    E[numEdge].next=H[u]; 
    H[u]=numEdge;
}


bool vis[10000];
int dis[10000],pre[10000],last[10000],flow[10000];//dis最小花费;pre每个点的前驱；last每个点的所连的前一条边；flow源点到此处的流量 
int maxflow,mincost;
queue <int> q; //保存的数据是点（从起点到终点） 


//使用深度优先DFS方法查找所有的增广路径 
int spfa(int s,int t){
    memset(dis,0x7f,sizeof(dis));
    memset(flow,0x7f,sizeof(flow));
    memset(vis,0,sizeof(vis));
    q.push(s); vis[s]=1; dis[s]=0; pre[t]=-1;

    while (!q.empty()) {
        int now=q.front(); q.pop();
        vis[now]=0; 
        for(int i=H[now]; i!=-1; i=E[i].next) {//从前端点now出发连着很多的后端点i 
            if(E[i].flow>0 && dis[E[i].to]>dis[now]+E[i].dis) { //第i条边还有余量，且会使费用更小 
                dis[E[i].to]=dis[now]+E[i].dis;
                pre[E[i].to]=now; //每个点所连的前端点是now 
                last[E[i].to]=i; //每个点的所连的前一条边 
                flow[E[i].to]=min(flow[now],E[i].flow);//最大流量取决于最小容量 
                if(!vis[E[i].to]) {
                    vis[E[i].to]=1;
                    q.push(E[i].to);
                }
            }
        }
    }
    return pre[t];
}


int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin>>M>>N;
    int sta=0, end=N+M*N+1; //“超级源点”和“超级结点”
    for(int i=1; i<=N; ++i) for(int j=1; j<=M; ++j){
        cin>>T[i][j];
    } 
    
    //构建网络图
    memset(H,-1,sizeof(H)), numEdge=-1; 
    for(int i=1; i<=N; ++i){
        AddEdge(sta, i, 1, 0); //从“超级源点”到“第i辆车” 
        AddEdge(i, sta, 0, 0);
        
        for(int j=1; j<=M; ++j) for(int k=1; k<=N; ++k){ 
            AddEdge(i, j*N+k, 1, k*T[i][j]); //从“第i辆车”到“第j个维修员修的倒数第k辆车”
            AddEdge(j*N+k, i, 0, -k*T[i][j]);
            if(i==N){
                AddEdge(j*N+k, end, 1, 0); //从“第j个维修员修的倒数第k辆车”到“超级结点” 
                AddEdge(end, j*N+k, 0, 0);
            }
        }
    }
    
    //求最大流最小费用 
    int maxflow=0, mincost=0;
    while(spfa(sta, end)!=-1) {  //迭代，不断的更新网络 
        maxflow+=flow[end];
        mincost+=flow[end]*dis[end];
        int now=end;
        while(now!=sta) {//从源点一直回溯到汇点 
            E[last[now]].flow-=flow[end];//flow和dis容易搞混 
            E[last[now]^1].flow+=flow[end];
            now=pre[now];
        }
    }
    cout<<mincost<<endl;
    return 0;
}