3.K近邻法

Posted 2020-11-26 xutianlun

1. k 近邻算法
k近邻法（k-nearest neighbor， k-NN） 是一种基本分类与回归方法。  k近邻法的输入为实例的特征向量， 对应于特征空间的点； 输出为实例的类别， 可以取多类。 k近邻法假设给定一个训练数据集， 其中的实例类别已定。 分类时， 对新的实例， 根据其k个最近邻的训练实例的类别， 通过多数表决等方式进行预测。因此， k近邻法不具有显式的学习过程。 k近邻法实际上利用训练数据集对特征向量空间进行划分， 并作为其分类的“模型”。 k值的选择、 距离度量及分类决策规则是k近邻法的三个基本要素。 k近邻法1968年由Cover和Hart提出。
算法（k近邻法）
输入： 训练数据集

其中， xi?x⊆Rn为实例的特征向量， yi? ＝{c1， c2,…,cK}为实例的类别， i＝1,2,…,N； 实例特征向量x；
输出： 实例x所属的类y。
（1） 根据给定的距离度量， 在训练集T中找出与x最邻近的k个点， 涵盖这k个点的x的邻域记作Nk(x)；
（2） 在Nk(x)中根据分类决策规则（如多数表决） 决定x的类别y：     

      

上式中， I为指示函数， 即当yi＝cj时I为1， 否则I为0。
k近邻法的特殊情况是k＝1的情形， 称为最近邻算法。 对于输入的实例点（特征向量） x， 最近邻法将训练数据集中与x最邻近点的类作为x的类。k近邻法没有显式的学习过程。

2. k 近邻模型
k近邻法使用的模型实际上对应于对特征空间的划分。 模型由三个基本要素——距离度量、 k值的选择和分类决策规则决定。

特征空间中两个实例点的距离是两个实例点相似程度的反映。 k近邻模型的特征空间一般是n维实数向量空间Rn。 使用的距离是欧氏距离， 但也可以是其他距离， 如更一般的Lp距离（Lp distance） 或Minkowski距离（Minkowski distance） 。设特征空间x是n维实数向量空间Rn，

xi,xj的Lp距离定义为：这里p≥1。

当p＝2时， 称为欧氏距离(Euclidean distance)， 即

当p＝1时， 称为曼哈顿距离（Manhattan distance） ， 即

当p＝时， 它是各个坐标距离的最大值， 即

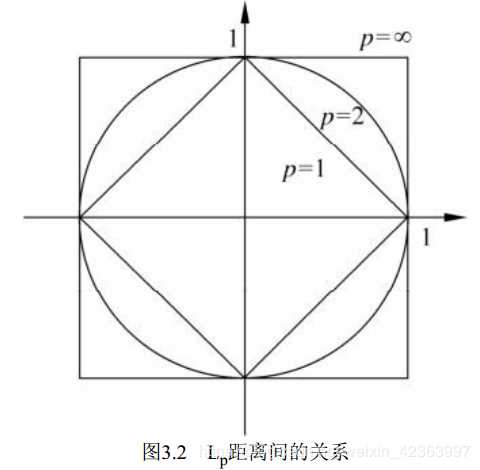
图3.2给出了二维空间中p取不同值时， 与原点的Lp距离为1（Lp＝1） 的点的图形。

k值的选择会对k近邻法的结果产生重大影响。
如果选择较小的k值， 就相当于用较小的邻域中的训练实例进行预测， “学习”的近似误差（approximation error） 会减小， 只有与输入实例较近的（相似的） 训练实例才会对预测结果起作用。 但缺点是“学习”的估计误差（estimation error） 会增大， 预测结果会对近邻的实例点非常敏感。 如果邻近的实例点恰巧是噪声， 预测就会出错。 换句话说， k值的减小就意味着整体模型变得复杂， 容易发生过拟合。
如果选择较大的k值， 就相当于用较大邻域中的训练实例进行预测。 其优点是可以减少学习的估计误差。 但缺点是学习的近似误差会增大。 这时与输入实例较远的（不相似的） 训练实例也会对预测起作用， 使预测发生错误。 k值的增大就意味着整体的模型变得简单。
k近邻法中的分类决策规则往往是多数表决， 即由输入实例的k个邻近的训练实例中的多数类决定输入实例的类。
多数表决规则（majority voting rule） 有如下解释： 如果分类的损失函数为0-1损失函数， 分类函数为

那么误分类的概率是。

对给定的实例x?x， 其最近邻的k个训练实例点构成集合Nk(x)。 如果涵盖Nk(x)的区域的类别是cj， 那么误分类率是要使误分类率最小即经验风险最小， 就要使

最大， 所以多数表决规则等价于经验风险最小化。

3. k 近邻法的实现： kd 树
kd树是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。kd树是二叉树， 表示对k维空间的一个划分（partition） 。 构造kd树相当于不断地用垂直于坐标轴的超平面将k维空间切分， 构成一系列的k维超矩形区域。 kd树的每个结点对应于一个k维超矩形区域。
构造平衡kd树
输入： k维空间数据集T＝{x1， x2,…,xN}，
其中 ， i＝1,2,…,N；
输出： kd树。
（1） 开始： 构造根结点， 根结点对应于包含T的k维空间的超矩形区域。
选择x(1)为坐标轴， 以T中所有实例的x(1)坐标的中位数为切分点， 将根结点对应的超矩形区域切分为两个子区域。 切分由通过切分点并与坐标轴x(1)垂直的超平面实现。由根结点生成深度为1的左、 右子结点： 左子结点对应坐标x(1)小于切分点的子区域，右子结点对应于坐标x(1)大于切分点的子区域。将落在切分超平面上的实例点保存在根结点。
（2） 重复： 对深度为j的结点， 选择x(l)为切分的坐标轴， l＝j(modk)+1， 以该结点的区域中所有实例的x(l)坐标的中位数为切分点， 将该结点对应的超矩形区域切分为两个子区域。 切分由通过切分点并与坐标轴x(l)垂直的超平面实现。由该结点生成深度为j+1的左、 右子结点： 左子结点对应坐标x(l)小于切分点的子区域， 右子结点对应坐标x(l)大于切分点的子区域。将落在切分超平面上的实例点保存在该结点。
（3） 直到两个子区域没有实例存在时停止。 从而形成kd树的区域划分。
代码：

# kd-tree每个结点中主要包含的数据结构如下 
class KdNode(object):
    def __init__(self, dom_elt, split, left, right):
        self.dom_elt = dom_elt  # k维向量节点(k维空间中的一个样本点)
        self.split = split      # 整数（进行分割维度的序号）
        self.left = left        # 该结点分割超平面左子空间构成的kd-tree
        self.right = right      # 该结点分割超平面右子空间构成的kd-tree
 
class KdTree(object):
    def __init__(self, data):
        k = len(data[0])  # 数据维度
        
        def CreateNode(split, data_set): # 按第split维划分数据集exset创建KdNode
            if not data_set:    # 数据集为空
                return None
            # key参数的值为一个函数，此函数只有一个参数且返回一个值用来进行比较
            # operator模块提供的itemgetter函数用于获取对象的哪些维的数据，参数为需要获取的数据在对象中的序号
            #data_set.sort(key=itemgetter(split)) # 按要进行分割的那一维数据排序
            data_set.sort(key=lambda x: x[split])
            split_pos = len(data_set) // 2      # //为Python中的整数除法
            median = data_set[split_pos]        # 中位数分割点             
            split_next = (split + 1) % k        # cycle coordinates
            
            # 递归的创建kd树
            return KdNode(median, split, 
                          CreateNode(split_next, data_set[:split_pos]),     # 创建左子树
                          CreateNode(split_next, data_set[split_pos + 1:])) # 创建右子树
                                
        self.root = CreateNode(0, data)         # 从第0维分量开始构建kd树,返回根节点

# KDTree的前序遍历
def preorder(root):  
    print (root.dom_elt)  
    if root.left:      # 节点不为空
        preorder(root.left)  
    if root.right:  
        preorder(root.right)    

用kd树的最近邻搜索
输入： 已构造的kd树； 目标点x；
输出： x的最近邻。
（1） 在kd树中找出包含目标点x的叶结点： 从根结点出发， 递归地向下访问kd树。 若目标点x当前维的坐标小于切分点的坐标， 则移动到左子结点， 否则移动到右子结点。 直到子结点为叶结点为止。
（2） 以此叶结点为“当前最近点”。
（3） 递归地向上回退， 在每个结点进行以下操作：
（a） 如果该结点保存的实例点比当前最近点距离目标点更近， 则以该实例点为“当前最近点”。
（b） 当前最近点一定存在于该结点一个子结点对应的区域。 检查该子结点的父结点的另一子结点对应的区域是否有更近的点。 具体地， 检查另一子结点对应的区域是否与以目标点为球心、 以目标点与“当前最近点”间的距离为半径的超球体相交。
如果相交， 可能在另一个子结点对应的区域内存在距目标点更近的点， 移动到另一个子结点。 接着， 递归地进行最近邻搜索；
如果不相交， 向上回退。
（4） 当回退到根结点时， 搜索结束。 最后的“当前最近点”即为x的最近邻点。
如果实例点是随机分布的， kd树搜索的平均计算复杂度是O(logN)， 这里N是训练实
例数。 kd树更适用于训练实例数远大于空间维数时的k近邻搜索。 当空间维数接近训练实
例数时， 它的效率会迅速下降， 几乎接近线性扫描。
代码：

# 对构建好的kd树进行搜索，寻找与目标点最近的样本点：
from math import sqrt
from collections import namedtuple

# 定义一个namedtuple,分别存放最近坐标点、最近距离和访问过的节点数
result = namedtuple("Result_tuple", "nearest_point  nearest_dist  nodes_visited")
  
def find_nearest(tree, point):
    k = len(point) # 数据维度
    def travel(kd_node, target, max_dist):
        if kd_node is None:     
            return result([0] * k, float("inf"), 0) # python中用float("inf")和float("-inf")表示正负无穷
 
        nodes_visited = 1
        
        s = kd_node.split        # 进行分割的维度
        pivot = kd_node.dom_elt  # 进行分割的“轴”
        
        if target[s] <= pivot[s]:           # 如果目标点第s维小于分割轴的对应值(目标离左子树更近)
            nearer_node  = kd_node.left     # 下一个访问节点为左子树根节点
            further_node = kd_node.right    # 同时记录下右子树
        else:                               # 目标离右子树更近
            nearer_node  = kd_node.right    # 下一个访问节点为右子树根节点
            further_node = kd_node.left
 
        temp1 = travel(nearer_node, target, max_dist)  # 进行遍历找到包含目标点的区域
        
        nearest = temp1.nearest_point       # 以此叶结点作为“当前最近点”
        dist = temp1.nearest_dist           # 更新最近距离
        
        nodes_visited += temp1.nodes_visited  
 
        if dist < max_dist:     
            max_dist = dist    # 最近点将在以目标点为球心，max_dist为半径的超球体内
            
        temp_dist = abs(pivot[s] - target[s])    # 第s维上目标点与分割超平面的距离
        if  max_dist < temp_dist:                # 判断超球体是否与超平面相交
            return result(nearest, dist, nodes_visited) # 不相交则可以直接返回，不用继续判断
            
        #----------------------------------------------------------------------  
        # 计算目标点与分割点的欧氏距离  
        temp_dist = sqrt(sum((p1 - p2) ** 2 for p1, p2 in zip(pivot, target)))     
        
        if temp_dist < dist:         # 如果“更近”
            nearest = pivot          # 更新最近点
            dist = temp_dist         # 更新最近距离
            max_dist = dist          # 更新超球体半径
        
        # 检查另一个子结点对应的区域是否有更近的点
        temp2 = travel(further_node, target, max_dist) 
        
        nodes_visited += temp2.nodes_visited
        if temp2.nearest_dist < dist:        # 如果另一个子结点内存在更近距离
            nearest = temp2.nearest_point    # 更新最近点
            dist = temp2.nearest_dist        # 更新最近距离
 
        return result(nearest, dist, nodes_visited)
 
    return travel(tree.root, point, float("inf"))  # 从根节点开始递归

p = inf为闵式距离minkowski_distance

例3.2 给定一个二维空间的数据集：

构造一个平衡kd树。

data = [[2,3],[5,4],[9,6],[4,7],[8,1],[7,2]]
kd = KdTree(data)
preorder(kd.root)

[7, 2]
[5, 4]
[2, 3]
[4, 7]
[9, 6]
[8, 1]
找出距离点[3,4.5]最近的点：

ret = find_nearest(kd, [3,4.5])
print (ret)

Result_tuple(nearest_point=[2, 3], nearest_dist=1.8027756377319946, nodes_visited=4)

本代码同样适用三维，使用方式一样。