前缀和&差分

Posted 2020-11-25 waryan

一：差分数组概念

 一、差分数组的定义及用途

1.定义：
对于已知有n个元素的数列d，建立记录它每项与前一项差值的差分数组f：显然，f[1]=d[1]-0=d[1];对于整数i∈[2,n]，我们让f[i]=d[i]-d[i-1]。//f[i]数组为差分数组,d[i]数组为原数组

2.简单性质：
(1)计算数列各项的值：观察d[2]=f[1]+f[2]=d[1]+d[2]-d[1]=d[2]可知，d[i]=f[i]的前缀和。
(2)计算数列每一项的前缀和：第i项的前缀和即为数列前i项的和，那么推导可知

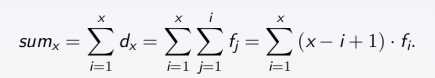//此处求的是d[i]数组的前缀和呼应3.(2)

即可用差分数组求出数列前缀和；

3.用途：
(1)快速处理区间加减操作：
对数列区间[L,R]中的每个数加上x，我们通过性质(1)知道，第一个受影响的差分数组中的元素为f[L],即令f[L]+=x，那么后面数列元素在计算过程中都会加上x；

最后一个受影响的差分数组中的元素为f[R],所以令f[R+1]-=x，即可保证不会影响到R以后数列元素的计算。

这样我们不必对区间内每一个数进行处理，只需处理两个差分后的数即可；

(2)询问区间和问题：
由性质(2)我们可以计算出数列各项的前缀和数组sum各项的值；那么显然，区间[L,R]的和即为ans=sum[R]-sum[L-1];

 

二：差分&前缀和模板题

#include<iostream>
#include<algorithm>
typedef long long ll;
using namespace std;
const ll maxn=100010;
ll p[maxn],a[maxn],b[maxn],c[maxn],ans[maxn];
int main()
{
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    ll n,m;
    cin>>n>>m;
    for(ll i=1;i<=m;++i)
        cin>>p[i];
    for(ll i=1;i<n;++i)
        cin>>a[i]>>b[i]>>c[i];
    for(ll i=1;i<m;++i)
    {
        if(p[i]>p[i+1])
            ans[p[i+1]]++,ans[p[i]]--;
        else ans[p[i]]++,ans[p[i+1]]--;
    }
    for(ll i=1;i<=n;++i)
        ans[i]+=ans[i-1];
    ll sum=0;
    for(ll i=1;i<n;++i)
        sum+=min(a[i]*ans[i],c[i]+b[i]*ans[i]);
    cout<<sum<<endl;
    return 0;
}

 

差分与前缀和互逆，求完差分后可以求前缀和得到修改后的数据