协方差矩阵
Posted klausage
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了协方差矩阵相关的知识,希望对你有一定的参考价值。
方差是用来度量随机变量X 与其均值E(X) 的偏离程度。
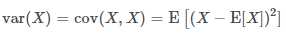
.png)
【随机变量的协方差】
在概率论和统计中,协方差是对两个随机变量联合分布线性相关程度的一种度量。两个随机变量越线性相关,协方差越大,完全线性无关,协方差为零。定义如下:

.png)
当X,Y是同一个随机变量时,XX与其自身的协方差就是XX的方差,可以说方差是协方差的一个特例:
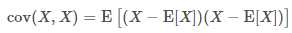
.png) 或者
或者.png)
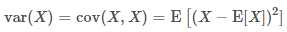
定义相关系数η为:
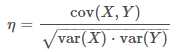
.png)
通过X的方差var?(X)与Y的方差var?(Y)对协方差cov?(X,Y)归一化,得到相关系数η,η的取值范围是[−1,1]。1表示完全线性相关,−1表示完全线性负相关,0表示线性无关。线性无关并不代表完全无关,更不代表相互独立。
【样本的协方差】
在实际中,通常我们手头会有一些样本,样本有多个属性,每个样本可以看成一个多维随机变量的样本点,我们需要分析两个维度之间的线性关系。协方差及相关系数是度量随机变量间线性关系的参数,由于不知道具体的分布,只能通过样本来进行估计。
设样本对应的多维随机变量为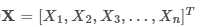
.png) ,样本集合为
,样本集合为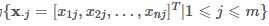
.png) ,m为样本数量。与样本方差的计算相似,a和b两个维度样本的协方差公式为,其中1?a?n,1?b?n,n为样本维度:
,m为样本数量。与样本方差的计算相似,a和b两个维度样本的协方差公式为,其中1?a?n,1?b?n,n为样本维度:
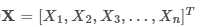
.png) ,样本集合为
,样本集合为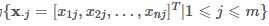
.png) ,m为样本数量。与样本方差的计算相似,a和b两个维度样本的协方差公式为,其中1?a?n,1?b?n,n为样本维度:
,m为样本数量。与样本方差的计算相似,a和b两个维度样本的协方差公式为,其中1?a?n,1?b?n,n为样本维度: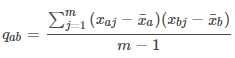
.png)
这里分母为m−1是因为随机变量的数学期望未知,以样本均值代替,自由度减一。
【多维随机变量的协方差矩阵】对多维随机变量.png)
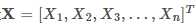 ,我们往往需要计算各维度两两之间的协方差,这样各协方差组成了一个n×n 的矩阵,称为协方差矩阵。协方差矩阵是个对称矩阵,对角线上的元素是各维度上随机变量的方差。我们定义协方差矩阵为 Σ,这个符号与求和 ∑相同,需要根据上下文区分。矩阵内的元素Σij为:
,我们往往需要计算各维度两两之间的协方差,这样各协方差组成了一个n×n 的矩阵,称为协方差矩阵。协方差矩阵是个对称矩阵,对角线上的元素是各维度上随机变量的方差。我们定义协方差矩阵为 Σ,这个符号与求和 ∑相同,需要根据上下文区分。矩阵内的元素Σij为:
.png)
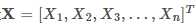 ,我们往往需要计算各维度两两之间的协方差,这样各协方差组成了一个n×n 的矩阵,称为协方差矩阵。协方差矩阵是个对称矩阵,对角线上的元素是各维度上随机变量的方差。我们定义协方差矩阵为 Σ,这个符号与求和 ∑相同,需要根据上下文区分。矩阵内的元素Σij为:
,我们往往需要计算各维度两两之间的协方差,这样各协方差组成了一个n×n 的矩阵,称为协方差矩阵。协方差矩阵是个对称矩阵,对角线上的元素是各维度上随机变量的方差。我们定义协方差矩阵为 Σ,这个符号与求和 ∑相同,需要根据上下文区分。矩阵内的元素Σij为: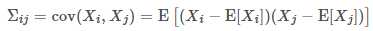
.png)
这样这个矩阵为:
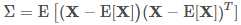
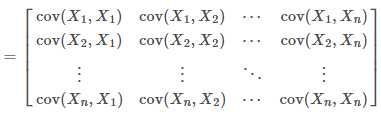
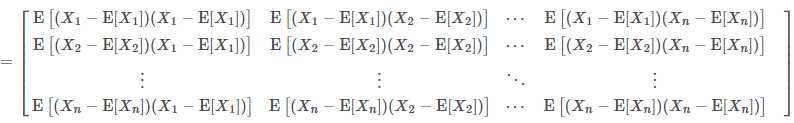
.png)
.png)
【样本的协方差矩阵】
与上面的协方差矩阵相同,只是矩阵内各元素以样本的协方差替换。样本集合为.png)
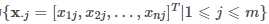 ,m为样本数量,所有样本可以表示成一个n×m 的矩阵。我们以
,m为样本数量,所有样本可以表示成一个n×m 的矩阵。我们以.png) 表示样本的协方差矩阵,与Σ区分。
表示样本的协方差矩阵,与Σ区分。
.png)
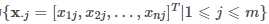 ,m为样本数量,所有样本可以表示成一个n×m 的矩阵。我们以
,m为样本数量,所有样本可以表示成一个n×m 的矩阵。我们以.png) 表示样本的协方差矩阵,与Σ区分。
表示样本的协方差矩阵,与Σ区分。
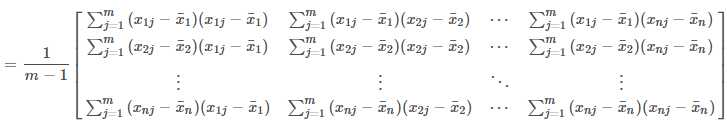
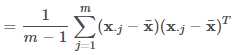
.png)
.png)
.png)
公式中m 为样本数量,x¯为样本的均值,是一个列向量,x⋅j 为第 j 个样本,也是一个列向量。
在写程序计算样本的协方差矩阵时,我们通常用后一种向量形式计算。一个原因是代码更紧凑清晰,另一个原因是计算机对矩阵及向量运算有大量的优化,效率高于在代码中计算每个元素。
需要注意的是,协方差矩阵是计算样本不同维度之间的协方差,而不是对不同样本计算,所以协方差矩阵的大小与维度相同。
以上是关于协方差矩阵的主要内容,如果未能解决你的问题,请参考以下文章