算法学习——离散化（整数离散化）

Posted 2020-11-25 flydoggie

百度百科解释：

离散化，把无限空间中有限的个体映射到有限的空间中去，以此提高算法的时空效率。

通俗的说，离散化是在不改变数据相对大小的条件下，对数据进行相应的缩小。例如：

原数据：1,999,100000,15；处理后：1,3,4,2；

原数据：{100,200}，{20,50000}，{1,400}；

处理后：{3,4}，{2,6}，{1,5}；

 

用我的理解来说，就是抠搜。当数据的范围很大很多，但是数据的数量不多时，我们通过映射的方法，把数据的存储范围进行压缩，舍弃掉不需要的空间，只留用到的空间。

简单举个例子：广场举行一个活动，根据人的岁数来领取对应的奖品。正常我们需要准备1-150岁共150份奖品，但是活动有条件限制，就是让你提前报名提交自己的岁数，所以我们得到了一个真实的数据，来领奖品的都是老头老大妈，岁数只有从60-80岁的，所以我们不需要准备150种奖品，我们只需要准备60-80岁这些会来的人的奖品就行。把[60,80]这些数据排序后映射到我们实际上准备的空间里。也就是离散化。

 

例题：

区间和

 

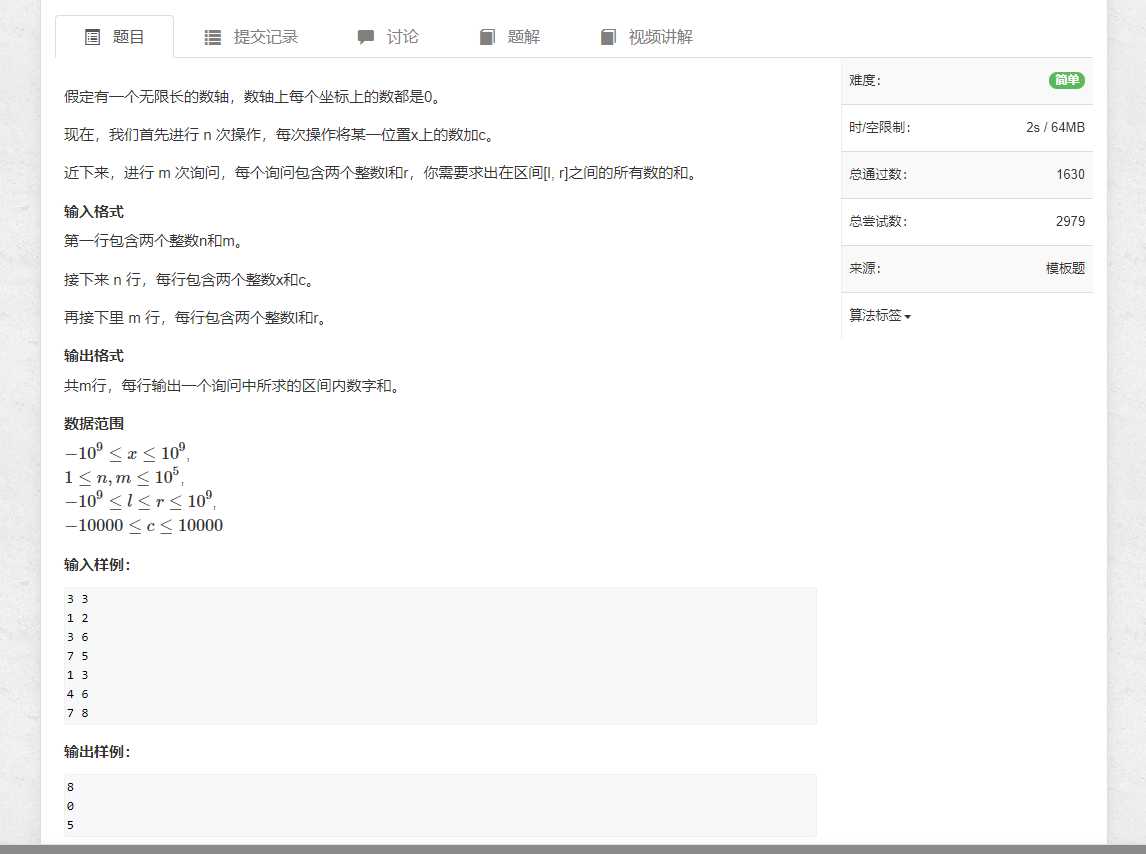
 这就是一个十分标准可以利用离散化来解答的题目。因为数据范围是-10^9 至 10^9，而数据数量只有10^5。

我们只需要把所有用到的坐标全部存储起来，将其排序之后一个一个离散化到一个新的坐标轴上，使数据直接相邻，节省了大量空间。

然后是代码实现：

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
typedef pair<int,int> PII;
const int N = 300010;
//离散化数组
vector<int>alls;
//存放了插入数值和查询区间两种操作所用到的坐标以及值
vector<PII>add,query;
//a[N]是离散化后存放value的数组,s[N]是离散化之后的下标对应的前缀和数组
int a[N],s[N];
int n,m;
//实现根据原坐标x寻找离散化后坐标的函数find
int find(int x){
    //二分模板
    int l = 0 , r = alls.size()-1;
    while(l < r){
        int mid = l + r >> 1;
        if(alls[mid] >= x){ r = mid; }
        else l = mid + 1;
    }
    return r+1 ;
}

int main(){
    //读入数据
    cin>>n>>m;
    //先读入需要插入的点的坐标和数值
    int x,c;
    for(int i = 0 ; i < n ; i ++){
        cin>>x>>c;
        //添加到对应的容器中存储;
        alls.push_back(x);
        add.push_back( {x,c} );
    }
    
    //再读入需要查询的区间的左右坐标
    int l,r;
    for(int i = 0 ; i < m ; i++ ){
        cin>>l>>r;
        alls.push_back(l);
        alls.push_back(r);
        query.push_back( {l,r} );
    }
    //对离散化数组进行排序和去重
    sort(alls.begin(),alls.end());
    alls.erase(unique(alls.begin(),alls.end()),alls.end());
   
   //处理插入操作
   for(auto it:add){
       int x = find(it.first);
       a[x] += it.second;
   }
   
   //预处理前缀和数组
   for(int i = 1 ;i <= alls.size() ; i ++)
       s[i] += s[i-1] + a[i];
       
   //执行查询操作
   for(auto it:query){
       int l = find(it.first);
       int r = find(it.second);
       cout<< s[r] - s[l - 1]<<endl;
   }
   
    
    return 0;
}