Laplacian Mesh Editing 拉普拉斯形变（待回学校更新）
Posted ivan-blog
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Laplacian Mesh Editing 拉普拉斯形变（待回学校更新）相关的知识，希望对你有一定的参考价值。
前言
因为实验需要用到拉普拉斯形变，但找了好久找到一个非常适合入门的资料。再此记录下我的学习过程，也算搬运翻译过来。
Introduction / Basic Laplacian Mesh Representation
主要思想，构造一个delta coordinates表示模型。
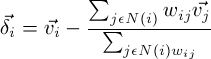
N(i)表示i的邻居，w_ij就是各种权重需要我们计算。如果权重全部是1，那么：
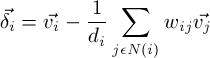
这里的d_i表示i的邻居个数。这种权重全为1的情况也叫做umberalla weighting
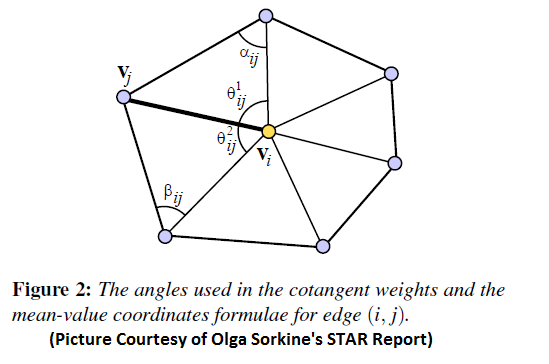
另外一种较出名的是cotangent weights
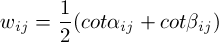
Mesh Reconstruction
待更新
Mesh Deformation
待更新
2D Parameterization
待更新
Membrane Surface
待更新
Surface Function Interpolation
待更新
Discrete Mean Curvature Approximation
待更新
Spectral Eigenanalysis
待更新
代码实现(python)
待更新
实验效果
待更新
以上是关于Laplacian Mesh Editing 拉普拉斯形变（待回学校更新）的主要内容，如果未能解决你的问题，请参考以下文章
拉普拉斯矩阵(Laplacian Matrix) 及半正定性证明