Tensorflow--梯度下降解决线性回归

Posted 2020-11-25 sccq

Tensorflow一些常见操作：

 代码：

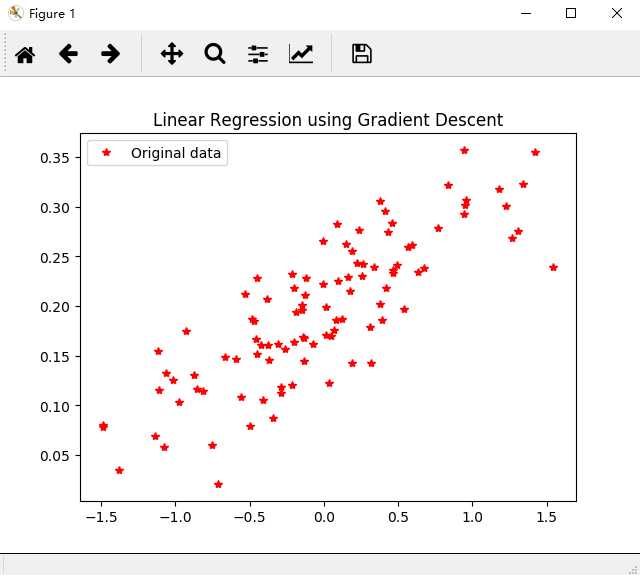
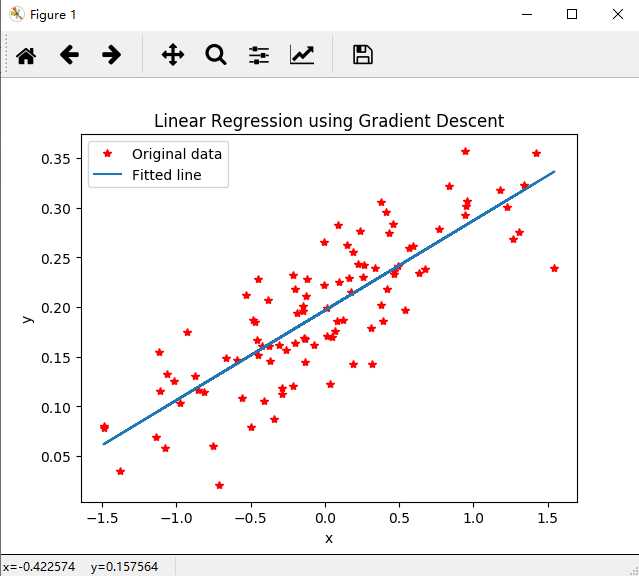
# -*- coding: UTF-8 -*-

"""
用梯度下降的优化方法来快速解决线性回归问题
"""

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf

try:
    xrange = xrange  # Python 2
except:
    xrange = range   # Python 3

# 构建数据
points_num = 100
vectors = []

# 用 Numpy 的正态随机分布函数生成 100 个点
# 这些点的（x, y）坐标值对应线性方程 y = 0.1 * x + 0.2
# 权重（Weight）为 0.1，偏差（Bias）为 0.2
for i in xrange(points_num):
    x1 = np.random.normal(0.0, 0.66)
    y1 = 0.1 * x1 + 0.2 + np.random.normal(0.0, 0.04)
    vectors.append([x1, y1])

x_data = [v[0] for v in vectors]  # 真实的点的 x 坐标
y_data = [v[1] for v in vectors]  # 真实的点的 y 坐标

# 图像 1 ：展示 100 个随机数据点
plt.plot(x_data, y_data, ‘r*‘, label="Original data")  # 红色星形的点
plt.title("Linear Regression using Gradient Descent")
plt.legend()
plt.show()

# 构建线性回归模型
W = tf.Variable(tf.random_uniform([1], -1.0, 1.0))  # 初始化 Weight
b = tf.Variable(tf.zeros([1]))                      # 初始化 Bias
y = W * x_data + b                                  # 模型计算出来的 y

# 定义 loss function（损失函数）或 cost function（代价函数）
# 对 Tensor 的所有维度计算 ((y - y_data) ^ 2) 之和 / N
loss = tf.reduce_mean(tf.square(y - y_data))

# 用梯度下降的优化器来最小化我们的 loss（损失）
optimizer = tf.train.GradientDescentOptimizer(0.5)  # 设置学习率为 0.5
train = optimizer.minimize(loss)

# 创建会话
sess = tf.Session()

# 初始化数据流图中的所有变量
init = tf.global_variables_initializer()
sess.run(init)

# 训练 20 步
for step in xrange(20):
    # 优化每一步
    sess.run(train)
    # 打印出每一步的损失，权重和偏差
    print("第 {} 步的 损失={}, 权重={}, 偏差={}".format(step+1, sess.run(loss), sess.run(W), sess.run(b)))

# 图像 2 ：绘制所有的点并且绘制出最佳拟合的直线
plt.plot(x_data, y_data, ‘r*‘, label="Original data")  # 红色星形的点
plt.title("Linear Regression using Gradient Descent")  # 标题，表示 "梯度下降解决线性回归"
plt.plot(x_data, sess.run(W) * x_data + sess.run(b), label="Fitted line")  # 拟合的线
plt.legend()
plt.xlabel(‘x‘)
plt.ylabel(‘y‘)
plt.show()

# 关闭会话
sess.close()

运行结果：

第 1 步的 损失=0.10736162215471268, 权重=[0.5780755], 偏差=[0.21398427]
第 2 步的 损失=0.03437836095690727, 权重=[0.36165723], 偏差=[0.20607387]
第 3 步的 损失=0.01180324051529169, 权重=[0.24128976], 偏差=[0.20176485]
第 4 步的 损失=0.004820318892598152, 权重=[0.17434561], 偏差=[0.19936827]
第 5 步的 损失=0.0026603667065501213, 权重=[0.13711363], 偏差=[0.19803537]
第 6 步的 损失=0.001992251491174102, 权重=[0.11640651], 偏差=[0.19729406]
第 7 步的 损失=0.0017855906626209617, 权重=[0.10488994], 偏差=[0.19688177]
第 8 步的 损失=0.0017216663109138608, 权重=[0.09848482], 偏差=[0.19665247]
第 9 步的 损失=0.0017018934013321996, 权重=[0.09492253], 偏差=[0.19652495]
第 10 步的 损失=0.001695777173154056, 权重=[0.0929413], 偏差=[0.19645402]
第 11 步的 损失=0.0016938853077590466, 权重=[0.09183941], 偏差=[0.19641456]
第 12 步的 损失=0.0016933002043515444, 权重=[0.09122658], 偏差=[0.19639263]
第 13 步的 损失=0.0016931190621107817, 权重=[0.09088574], 偏差=[0.19638042]
第 14 步的 损失=0.0016930631827563047, 权重=[0.09069619], 偏差=[0.19637364]
第 15 步的 损失=0.0016930458368733525, 权重=[0.09059076], 偏差=[0.19636987]
第 16 步的 损失=0.0016930404817685485, 权重=[0.09053212], 偏差=[0.19636777]
第 17 步的 损失=0.001693038735538721, 权重=[0.09049951], 偏差=[0.1963666]
第 18 步的 损失=0.0016930383862927556, 权重=[0.09048138], 偏差=[0.19636595]
第 19 步的 损失=0.0016930380370467901, 权重=[0.09047129], 偏差=[0.1963656]
第 20 步的 损失=0.0016930379206314683, 权重=[0.09046568], 偏差=[0.19636539]