17-快速排序

Posted 2020-11-25 liujiaqi1101

参考和引用了 白话经典算法系列之六——快速排序 的一些内容

1. 简单介绍

• 快速排序(Quicksort) 是一种分治的排序算法，它将一个数组分成两个子数组，将两部分独立地排序；排序的方式是当两个子数组都有序时整个数组也就自然有序了
• 通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列

2. 思想

2.1 切分元素 arr[x]

• 该元素值又被称为"基准数" / "中轴"
• 一般选取数组首元素、尾元素、中间元素 作为切分元素
• 作用：将数组分割成两个子数组，其中一个子数组的元素都比基准数小，另一个子数组的元素都比基准数要大

2.2 切分方法 partition(arr, left, right)

• 快速排序递归地将子数组arr{left, right}排序，每调用一次 partition 就会使 基准数arr[x] 放到最终位置，然后再递归调用 partition 将其他位置的元素排序
• 切分过程 使得数组满足下面3个条件:
  • 对于某个x, arr[x] 已经排定
  • arr[left] 到 arr[x-1] 的所有元素都小于 arr[x]
  • arr[x+1] 到 arr[right] 的所有元素都不小于 arr[x]
• 因为切分过程总是能排定一个元素，用归纳法不难证明递归能够正确地将数组排序：如果左子数组和右子数组都是有序的，那么左子数组(有序且没有任何元素大于切分元素)、切分元素和右子数组(有序且没有任何元素小于切分元素)组成的结果数组也一定是有序的。切分算法就是实现了这个思路的一个递归程序

2.3 基本思想

1. 先从数组中选定一个切分元素作为基准数
2. 分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边
3. 再对左右区间重复step2，直到各区间只有一个数

2.4 举例

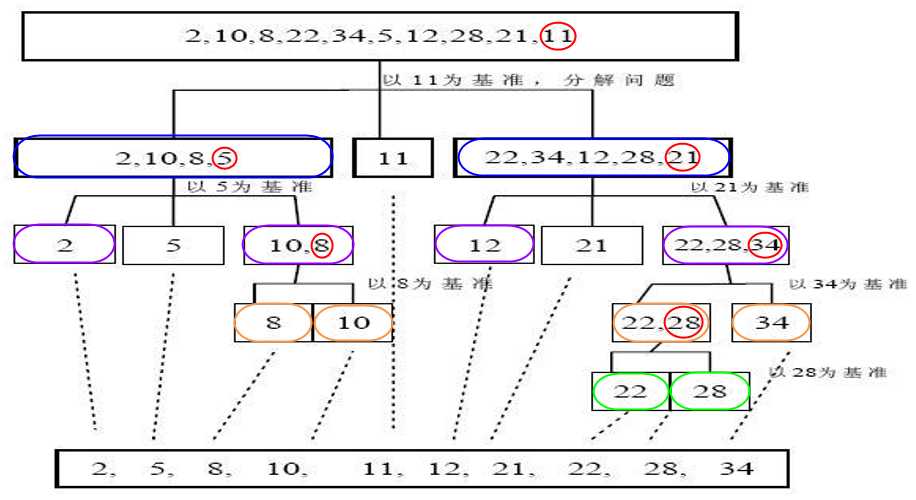
2.5 挖坑填数

挖坑填数过程详见文首所引用的那片文章

1. i = left, j = right; 将基准数挖出而形成了第一个坑arr[i]
2. j-- 由后向前找比基准数小的数，找到后挖出此数填入前面一个坑arr[i]中
3. i++ 由前向后找比基准数大的数，找到后也挖出来填到前面一个坑arr[j]中
4. 再重复执行step2，step3两步，直到i == j，将基准数填入a[i]中

3. 代码实现

public class QuickSortDemo {
    public static void main(String[] args) {
        int[] arr = {5, 9, 78, 0, 23, -567, 70, 42, -5, 36};
        quickSort(arr, 0, arr.length-1);
        System.out.println(Arrays.toString(arr));
    }
    
    public static void quickSort(int[] arr, int left, int right) {
        // 分治
        if(left < right) {
            int x = partition(arr, left, right);
            quickSort(arr, left, x-1);
            quickSort(arr, x+1, right);
        }
    }
    
    /**
     * 递归调用切分方法完成子数组排序
     * @param arr 待排序数组
     * @param left 数组首元素索引
     * @param right 数组尾元素索引
     * @return 切分元素的最终存放位置
     */
    public static int partition(int[] arr, int left, int right) {
        int i = left;
        int j = right;
        int pivot = arr[i];
        
        while(i < j) {
            // 1. 从右向左找 小于 pivot的数来填arr[i]的坑
            while(i < j && arr[j] >= pivot)
                j--;
            if(i < j) {
                arr[i] = arr[j];
                i++;
            }
            // 2. 从左向右找 大于|等于 pivot的数来填arr[j]的坑
            while(i < j && arr[i] < pivot)
                i++;
            if(i < j) {
                arr[j] = arr[i];
                j--;
            }
        }
        
        // 退出时, i和j相遇; 该位置也是pivot在数组中的最终位置
        arr[i] = pivot;
        return i;
    }
}