在 大家的做题热情实在是高 故开新帖继续做题 中 的 回复
Posted ksongking
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了在 大家的做题热情实在是高 故开新帖继续做题 中 的 回复相关的知识,希望对你有一定的参考价值。
本文 是 《做一道 高一 求 函数 值域 的 题》 https://www.cnblogs.com/KSongKing/p/12233398.html 的 续篇, 呵呵呵呵 。
《做一道 高一 求 函数 值域 的 题》 里 做的 是 网友 暮色星辰ing (Suzuha) 先前发的 一个 贴 里的 题, 这个 帖 是 《高一狗流下了泪水 求大佬帮助》 , 不过 这个 帖 已经 被 Suzuha 自己 删了, 据说是 “问题解决了, 就把 帖 删了 。” , 不过 这个 帖 的 名字 很有意思, 就 记录一下 。
在 《做一道 高一 求 函数 值域 的 题》 的 结尾, 我说了 Suzuha 又 发了 一个 帖 《大家的做题热情实在是高 故开新帖继续做题》 http://tieba.baidu.com/p/6460902864 , 出了一个 新的 题 , 我们来 做做 这个 题 。
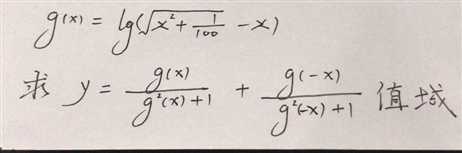
以下 是 在 帖 中 的 回复 :
14 楼
我也 化简 到 y = t / ( t^2 + 1 ) - ( t + 2) / [ ( t + 2)^2 + 1 ] ,
如果 令 u = t + 2, 则 y = t / ( t^2 + 1 ) - u / ( u^2 + 1 ) ,
然后 ?
Suzuha: 对啊←_← 然后发现不会写了
K歌之王: 回复 Suzuha :x 的定义域 是 ( - 负无穷 , 正无穷 ) ?
渝中寿人: 直接求导y‘=0,解出一个根t=-1,而t=g(x)=-1,解出x=0,y=-1。
渝中寿人: 也可以令t=g(x)=tanθ,t+2=g(x)+2=tanθ+2=tanα。看有没有办法?
K歌之王: 回复 渝中寿人 :求导 ……
16 楼
当 x = 0 时, t = -1, y = -1 ,
当 x = 正无穷 时, t = 负无穷, y = 0,
当 x = 负无穷 时, t = 正无穷, y = 0,
所以, y ∈ [ -1 , 0 ) , 不知道 对不对, 还要 想一下 。
K歌之王: 有问题, 从 y = -1 会 增长 到 大于 0 的一定数值, 然后 又 趋于 0 。
17 楼
y = t / ( t^2 + 1 ) - ( t + 2) / [ ( t + 2)^2 + 1 ] 对于 t 的 导数 可以求, 是一个 分式 求导, 但是 多项式 的 项数 太多, 不想求了, 求出来 以后 解 导数 = 0 的 方程 可能是一个 高次方程,
我假设 这个 方程 没有 常数项,那么 就有一个 解 是 t = 0, 就 假设 t = 0 时 产生 极值, 来 求求 t = 0 时 的 x 和 y, 求得 x = -0.495, y = 0.6,
0.6 和 楼主给出的 0.21 还是 有 比较大 的 差距 的 。
18 楼
追影入梦 :

Suzuha: 大神啊 奈何没学过求导 只能自学求求看了
K歌之王: 回复 Suzuha :这是 高中题 ?
Suzuha: 回复 K歌之王 :是
K歌之王: 回复 Suzuha : 不知道 还有没有 技巧性 的 解法 。
19 楼
ylyyjjlh2 :
哎呀,我把1/100看成1/1000了,应该为-1--0.2071068
ylyyjjlh2: xmin=0,xmax=7.8762725
20 楼
渝中寿人 :
故y∈[(-1-√2)/2,-1],或y∈(0,(-1+√2)/2]。over!
渝中寿人: 未必!不是偶函数啊!
渝中寿人: 我用极限法来部分解题。 g(x)=lg[(x^2)+0.01]^0.5-x =lg{x[1+1/(10x)^2]^0.5}-x =lg{x[1+1/2×1/(100x^2)]}-x (x→+∞) =lg[x+1/(200x)]-x
渝中寿人: g(-x)=lg[x+1/(200x)]+x (x→+∞)
渝中寿人: 打错了。
渝中寿人: g(x)=lg[1/(200x)](x→+∞) g(-x)=lg[2x+1/(200x)](x→+∞)
渝中寿人: y=1/[g(x)+1/g(x)]+1/[g(-x)+1/g(-x)] (x→+∞) 代入后取极限得y→0,则x→+∞,y→0(y>0)。
21 楼
ylyyjjlh2 :
好吧,我把图像也释放出来,别范那些低级错误了。
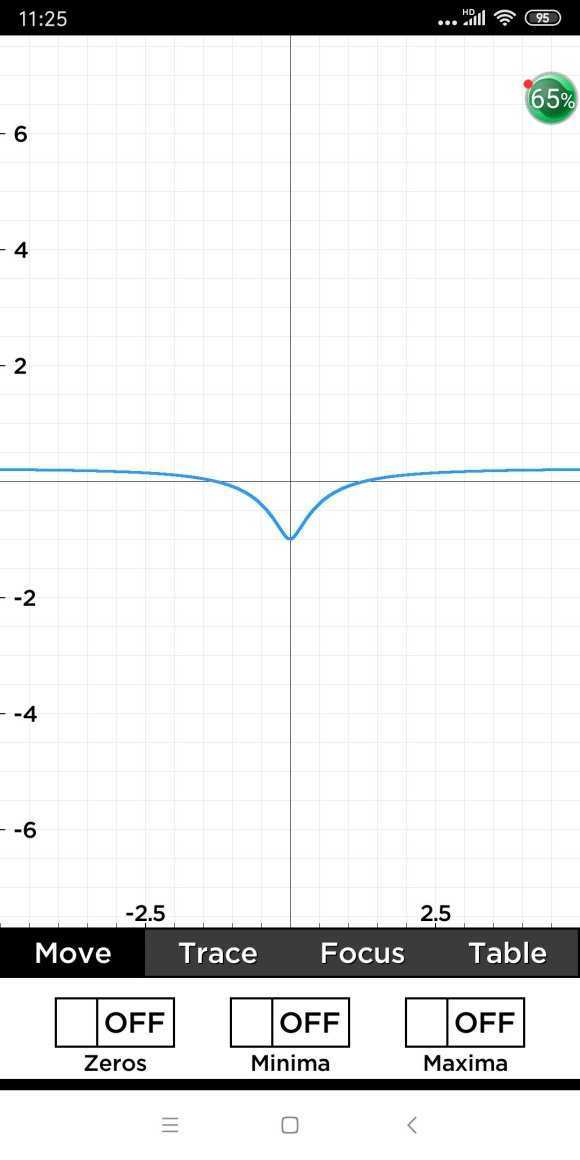
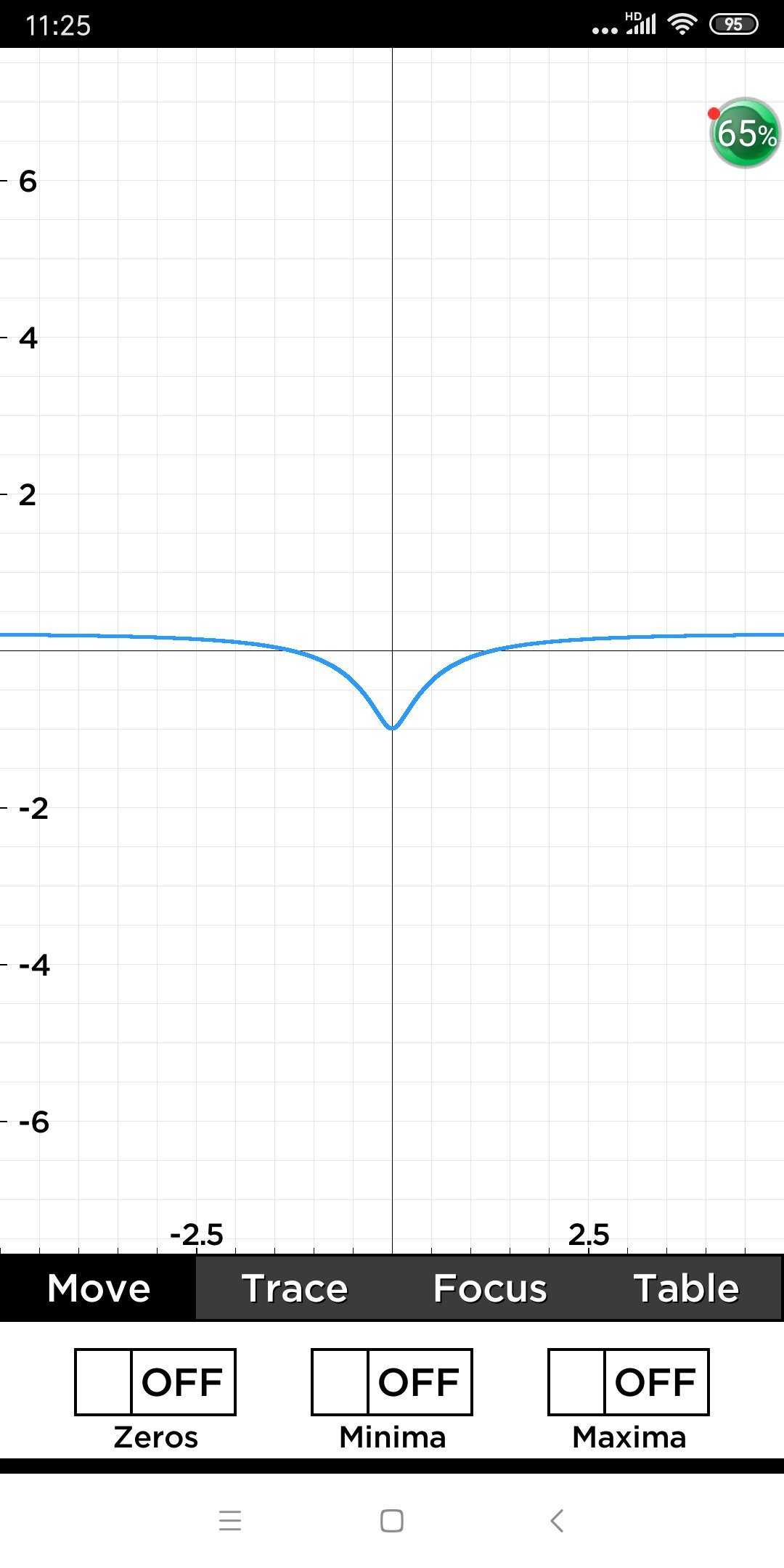
以上是关于在 大家的做题热情实在是高 故开新帖继续做题 中 的 回复的主要内容,如果未能解决你的问题,请参考以下文章