堆排序

Posted 2020-11-25 lijianming180

堆排序算法。

堆

堆又被称为优先队列。按照元素的优先级取出元素。

普通队列：先进先出；后进后出

优先队列：出队顺序和入队顺序无关；和优先级相关

在优先队列的内部，元素的次序却是由”优先级”来决定的：高优先级的元素排在队首，而低优先级的元素排在后面。优先队列入队操作比较复杂，需要将元素根据优先级尽量排到队列前面。

一个实现优先队列的经典方法是采用二叉堆(Binary Heap)。二叉堆将优先队列的入队和出队复杂度都保持在O(logn)。

动态选择优先队列。

关键词：动态

为什么使用优先队列？

在100000个元素中选择前100名？

在N个元素中选择前M个元素

优先队列 NlogM

入队和出队

二叉堆 Binary Heap

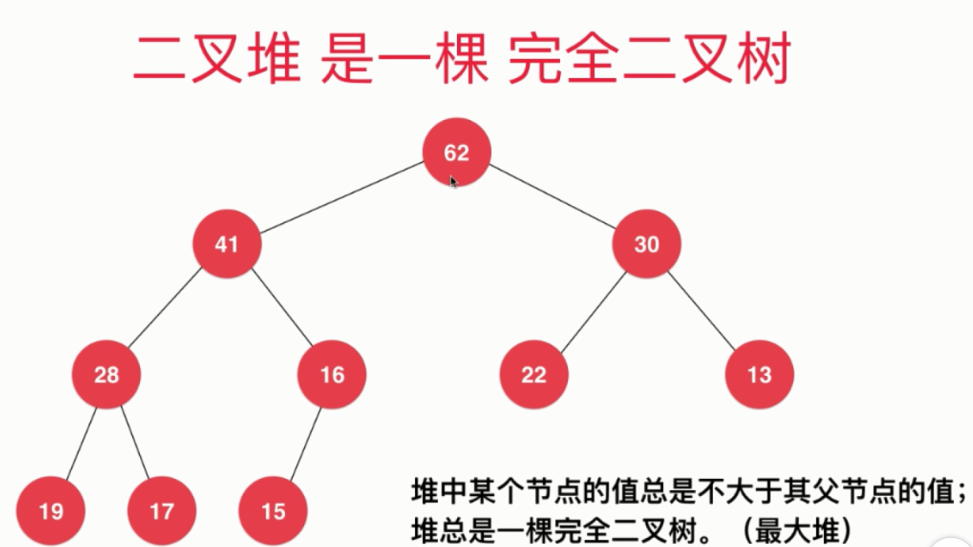
二叉堆是一棵完全二叉树。二叉堆有两种：键值总是最小的排在队首称为”最小堆”，反之，键值总是最大的排在队首称为最大堆。

堆中某个节点的值总是不大于其父节点的值。

堆总是一个完全二叉树。

最大堆，树顶的元素最大。

层数越高，数值越大。

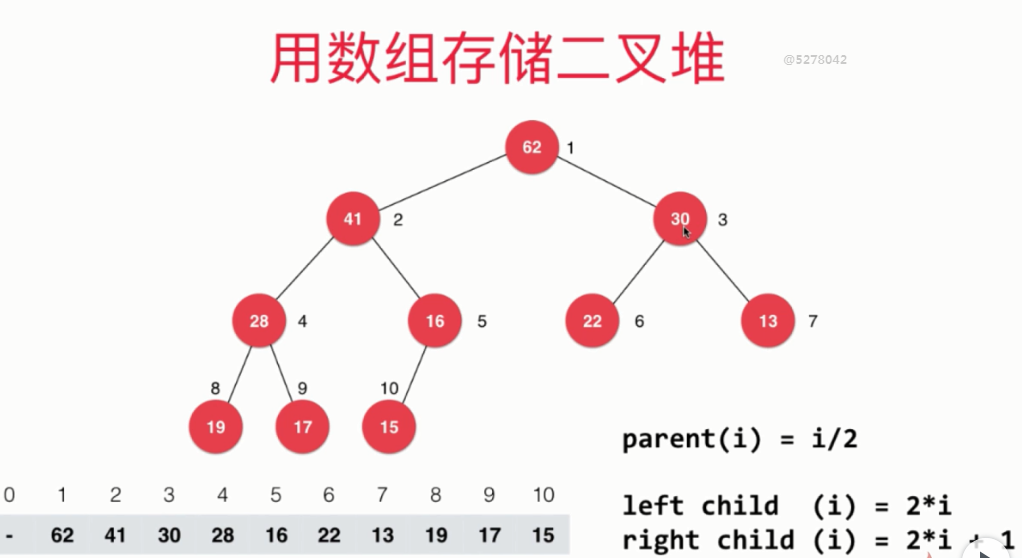
用数组存储二叉堆。

给每一个节点标记数字。

数组进行存储二叉堆。

其中的父节点和左节点、右节点的关系。

parent(i) = i/2  父节点等于子节点除于2
left child (i) 2 * i
right child (i) = 2*i +1 

二叉堆的操作

• BinaryHeap()：创建一个空的二叉堆对象

• insert(k)：将新元素加入到堆中

• findMin()：返回堆中的最小项，最小项仍保留在堆中

• delMin()：返回堆中的最小项，同时从堆中删除

• isEmpty()：返回堆是否为空

• size()：返回堆中节点的个数

• buildHeap(list)：从一个包含节点的列表里创建新堆

二叉堆结构性质

满二叉树

满二叉树：如果每一层的结点都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为k，且结点总数为(2^k)-1，则它就是满二叉树。

完全二叉树

完全二叉树：叶节点只能出现在最下层和次下层，并且最下面一层的节点都集中在该层最左边的若干位置的二叉树。

若二叉树的深度为h，除第h层外，其他各层(1~h-1)的结点数都达到最大个数，第h层所有的结点都连续集中在左边，这就是完全二叉树。

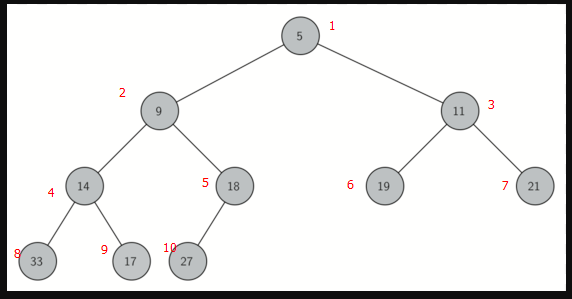
图 1：完全二叉树

可以使用单个列表实现完全二叉树，不需要使用节点，引用或嵌套列表。对于完全二叉树，如果节点在列表中的下标为p，其左节点下标为2p，右节点为2p+1。如果我们寻找任何结点的父节点时，可以使用python的整除，如果节点在列表中下标为n，那么父节点下标为n//2。

图2所示是一个完全二叉树和树的列表表示法。

父节点 p
左节点 2p
右节点 2p+1

完全树的列表表示法结合了完全二叉树的特性，使我们能够使用简单的数学方法高效地遍历一棵完全树。这也使我们高效实现二叉堆。

堆次序的性质

在堆里存储元素的方法依赖于堆的次序。堆次序，指堆中任何一个节点x，其父节点p的键值均小于或等于x的键值。

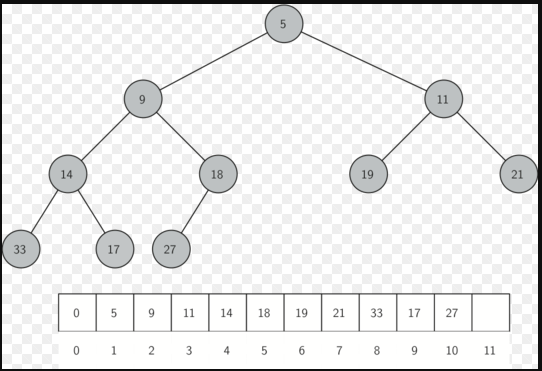
图2 ： 完全树和它的列表表示法

二叉堆操作的实现

构造二叉堆。采用一个列表保存堆的数据，构造函数只需要初始化一个列表和一个currentSize来表示堆当前的大小。Listing 1所示的是构造二叉堆的python代码。

Listing 1 构造二叉堆

class BinHeap:
    def __init__(self):
        self.heapList = [0]
        self.currentSize = 0 

接下来实现的是insert方法，为了满足“完全二叉树”的性质，新键值应该添加到列表的末尾。但是新键值简单的添加到列表末尾，显然无法满足堆次序。需要进行比较，找到合适的位置。可以通过比较父节点和新加入的元素的方法来重新满足堆次序。如果新加入的元素比父节点要小，可以与父节点互换位置。图 3 所示的是一系列交换操作来使新加入元素“上浮”到正确的位置。

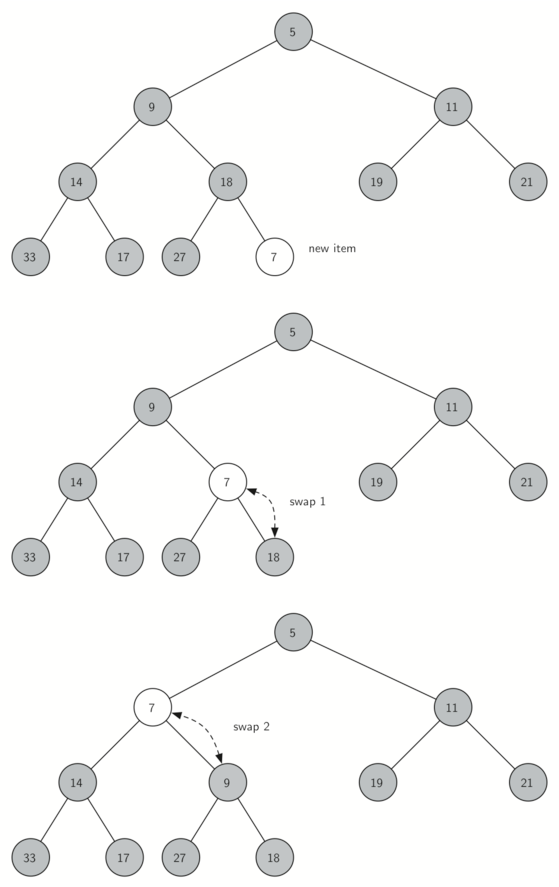
让一个元素”上浮”时，必须保证新节点和父节点以及其他兄弟节点之间的堆次序。如果新节点非常小的话，仍然需要将它交换到其他层。需要不断交换，直到到达树的顶端。Listing 2就是上浮方法，把一个新节点上浮到其正确的位置来满足堆次序。这里很好体现到了headlist中没有用到0的重要性。这里只需要做简单的整除，将当前节点的下标除以2，就可以计算出任何节点的父节点。

在Listing 3中，是insert方法的代码。insert里面很大一部分是由percUp函数完成的。当添加新节点时，调用percUp就可以将新节点放到正确的位置上。

Listing 2 上浮函数

def percUp(self,i):
        while i // 2 > 0:
            if self.heapList[i] < self.heapList[i // 2]:  #如果小于父节点的话就交换
                tmp = self.heapList[ i // 2]
                self.heapList[i // 2] = self.heapList[i]
                self.heapList[i] = tmp 
                #self.heapList[i // 2],self.heapList[i] = self.heapList[i],self.heapList[i // 2]
            i = i // 2

Listing 3 插入函数

def insert(self,k):
        self.heapList.append(k)   # 添加到后面
        self.currentSize = self.currentSize + 1 #长度加 1
        self.percUp(self.currentSize)     #调用上浮函数，

已经写好了insert方法，再来写delMin方法。delMin()：返回堆中的最小项，同时从堆中删除。堆次序要求根节点是树中的最小元素，很容易找到最小项。难点在于移走根节点的元素后如何保持堆结构和堆次序。

两步走。

1. 用最后一个节点代替根节点。移走最后一个节点保持了堆结构的性质。这是简单的替换，但是会破坏堆次序。
2. 将新节点下沉来恢复堆次序。图4所示是一系列交换操作来使新节点下沉到正确的位置。

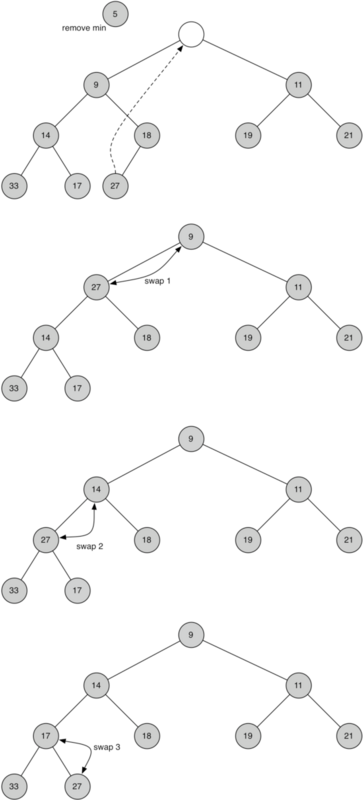
为了保持堆次序，需要将新的根节点沿着一条路径下沉，直到比两个子节点都小。在选择下沉路径时，如果新根节点比子节点大，那么选择较小的子节点与之交换。Listing 4所示的是新节点下沉所需的percDown和minChild方法的代码。

Listing 4

def percDown(self,i):
        while (i * 2) <= self.currentSize:
            mc = self.minChild(i)
            if self.heapList[i] > self.heapList[mc]:
                tmp = self.heapList[i]
                self.heapList[i] = self.heapList[mc]
                self.heapList[mc] = tmp 
            i = mc 

    def minChild(self,i):
        if i * 2 + 1 > self.currentSize:
            return i * 2 
        else:
            if self.heapList[i*2] < self.heapList[i*2+1]:
                return i*2 
            else:
                return i*2+1

大专栏  堆排序#Listing-5-delMin-代码-删除根节点" class="headerlink" title="Listing 5 delMin 代码 删除根节点">Listing 5 delMin 代码 删除根节点

def delMin(self):
        retval = self.heapList[1]
        self.heapList[1] = self.heapList[self.currentSize]
        self.currentSize = self.currentSize - 1
        self.heapList.pop()
        self.percDown(1)
        return retval

Listing 6

关于二叉堆的最后一部分便是找到从无需列表生成一个堆的方法。将无需列表中的每个元素依次插入堆中。对于一个排好序的列表，可以使用二分搜索找到合适的位置，然后在下一个位置插入这个键值到堆中，时间复杂度为O(logn)。另外插入一个元素到列表中需要将列表的一些其他元素移动，为新节点腾出位置，时间复杂度为O(n)，因此insert方法的总开销为O(nlogn)。其实可以直接将整个列表生成堆，将复杂度控制为O(n)。Listing 6所示的是生成堆的操作。

def buildHeap(self,alist):
        i = len(alist) // 2 
        self.currentSize = len(alist)
        self.heapList = [0] + alist[:]
        while (i>0):
            self.percDown(i)
            i = i - 1

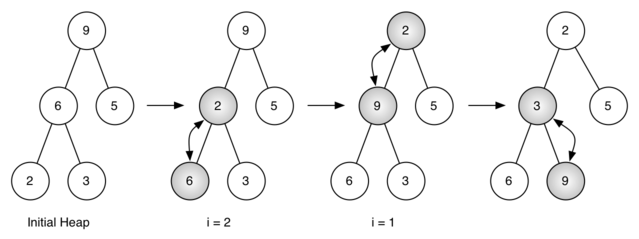
图5：将列表[9,6,5,2,3]生成一个二叉堆

图5是利用buildHeap方法将最开始的树[9,6,5,2,3]中的节点移动到正确的位置时所做的交换操作。尽管从树中间开始，然后回溯到根节点，但percDown方法保证了最大子节点总是下沉。因为堆是完全二叉树，任何在中间的节点都是叶节点，因此没有子节点。当i=1时，从根节点下沉，需要进行大量的交换操作。可以看到图5最右边的两棵树，首先9从根节点的位置移走，移到下一层级后，percDown进一步检查此时的子节点，保证它下降到不能在下降为止，即下降到正确的位置。然后进行第二次交换，9和3交换，由于9已经到了树最底层的层级，无法进一步交换了。比较一下列表表示法和图5所示的树表示法进行一系列的交换。

i = 2  [0, 9, 5, 6, 2, 3]
i = 1  [0, 9, 2, 6, 5, 3]
i = 0  [0, 2, 3, 6, 5, 9]

完整代码

# -*- coding:utf-8 -*-

class BinHeap:
    def __init__(self):
        self.heapList = [0]
        self.currentSize = 0


    def percUp(self,i):
        while i // 2 > 0:
            if self.heapList[i] < self.heapList[i // 2]:  #如果小于父节点的话就交换
                tmp = self.heapList[ i // 2]
                self.heapList[i // 2] = self.heapList[i]
                self.heapList[i] = tmp 
                #self.heapList[i // 2],self.heapList[i] = self.heapList[i],self.heapList[i // 2]
            i = i // 2


    def insert(self,k):
        self.heapList.append(k)   # 添加到后面
        self.currentSize = self.currentSize + 1 #长度加 1
        self.percUp(self.currentSize)     #调用上浮函数，


    def percDown(self,i):   #将i索引的值向下移动
        # i 节点应该有孩子，在完全二叉树中，只要有左节点，就一定有孩子
        while (i * 2) <= self.currentSize:  #完全二叉树，不可能只有右节点，而没有左节点
            mc = self.minChild(i) #调用 minChild函数，取得最小的孩子节点
            if self.heapList[i] > self.heapList[mc]:  #如果父节点大于子节点，进行替换
                tmp = self.heapList[i]
                self.heapList[i] = self.heapList[mc]
                self.heapList[mc] = tmp 
            i = mc  #把该位置进行替换

    def minChild(self,i):       #寻找小的子节点
        if i * 2 + 1 > self.currentSize:  #判断是否有右节点
            return i * 2 
        else:
            if self.heapList[i*2] < self.heapList[i*2+1]: #左节点和右节点的比较。如果左节点小，则返回左节点。父节点和子节点替换，需要在子节点中找到最小的那一个进行替换
                return i*2 
            else:
                return i*2+1


    def delMin(self):
        retval = self.heapList[1]      #取出堆中的第一个元素
        self.heapList[1] = self.heapList[self.currentSize]   #把堆中的最后一个元素放到第一个位置
        self.currentSize = self.currentSize - 1   #堆的长度减1
        self.heapList.pop()    #删除最后的元素，因为已经移到了第一个位置
        self.percDown(1)    #将根节点的值进行下移
        return retval   #返回取出的元素

    def buildHeap(self,alist):       
        i = len(alist) // 2    # i 为 列表的长度除于 2
        self.currentSize = len(alist)     #堆长度为列表长度
        self.heapList = [0] + alist[:]   #添加到堆中
        while (i>0):
            self.percDown(i)     #下移
            i = i - 1

bh = BinHeap()
bh.buildHeap([9,5,6,2,3])

print bh.delMin()            
print bh.delMin() 
print bh.delMin() 
print bh.delMin() 
print bh.delMin()                 

输出结果为：

C:UsersAdministratorDesktopAlgo>python2 heap.py
2
3
5
6
9                

二叉堆(二)

参考

tree

import math


class ArrBinHeap():
    def __init__(self):
        self._data = []  # 数组表示堆

    def insert(self, val):
        self._data.append(val)
        self.bubble_up(len(self._data) - 1)

    def bubble_up(self, i):
        pass

    def pop(self):
        # 删除根节点的方法，把数组的最后一个元素和根节点替换，进行下移
        last_index = len(self._data) - 1  # 最后一个节点的位置
        last_data = self._data[last_index]  # 读取最后一个节点的值
        self._data = self._data[:last_index]  # 删掉最后一个节点
        self._data[0] = last_data
        self.bubble_down(0)

    def bubble_down(self, i):
        pass

    def lchild(self, i):
        index = 2 * i + 1
        # 检查是否超出范围
        if len(self._data) < index:
            return -1
        return index

    def rchild(self, i):
        index = 2 * i + 2
        # 检查是否超出范围
        if len(self._data) < index:
            return -1
        return index

    def parent(self, i):
        # 超找父节点
        return math.floor((i + 1) / 2)

class MaxBinHeap(ArrBinHeap):
    # 最大堆
    def __init__(self):
        super(MaxBinHeap,self).__init__()

    def bubble_up(self, i):
        # 父节点
        p_index = self.parent(i)

        if p_index == -1:  #没有父节点，返回最顶层
            return True
        #如果父节点比当前节点更小，交换这两个节点的数据
        p_data = self._data[p_index]  #父节点值
        data = self._data[i]  #插入位置值
        if p_data < data:
            self._data[i] = p_data
            self._data[p_index] = data
            #再进行一次bubble_up
            self.bubble_up(p_index)  #递归执行
        return True

    def bubble_down(self, i):
        lc_index = self.lchild(i)  # 左节点
        rc_index = self.rchild(i)  #右节点
        if not (lc_index == -1 and rc_index == -1):
            # 存在左右节点
            #选择最大的子节点
            if rc_index == -1 or(self._data[lc_index] > self._data[rc_index]):
                # 右节点不存在，或者左节点大于右节点
                rep_index = lc_index
            elif lc_index == -1 or (self._data[lc_index] < self._data[rc_index]):
                rep_index = rc_index
            rep_data = self._data[rep_index]
            data = self._data[i]
            if rep_data > data:
                self._data[rep_index] = data
                self._data[i] = rep_data
                self.bubble_down(rep_index)
        else:
            return True
        return True

main.py

from tree import MaxBinHeap
import math
import time
from random import randint

def build_heap(total_num): 
    #先创建一个堆，一个个的插入进去
    # o (nlogn)
    heap = MaxBinHeap()
    for i in range(total_num):
        heap.insert(randint(0,total_num))
    return heap


def build_off_heap(total_num):
    heap = MaxBinHeap()
    # o(n) sfa
    for i in range(total_num):
        heap._data.append(randint(0,total_num))
    for i in range(math.floor(len(heap._data) / 2 )+1,+1,+1):
       heap.bubble_down(i)
    return heap

if __name__ == '__main__':
    start_time = time.time()
    heap = build_heap(10000)
    print("---- build_heap %s seconds ----" % (time.time() - start_time))

    start_time = time.time()
    off_heap = build_off_heap(10000)
    print("----%s seconds ----" % (time.time() - start_time)

参考

Python数据结构——二叉堆的实现

Python数据结构与算法设计总结篇

Binary Heap Operations

堆和索引堆的python实现

堆与堆排序，最大索引堆（python实现）