行列式概念和性质-总结

Posted 2020-11-25 baobobbyzhang

• 把n各不同的元素排成一列，叫做这n个元素的全排列，对于n个不同的元素，先规定各元素之间有一个标准次序，于是在这n个元素的任一排列中，当某两个元素的先后次序玉标准次序不同时，就说有一个逆序。一个排列中所有逆序的总数叫做这个排列的逆序数。逆序数为奇数的排列叫做奇排列，逆序数为偶数的排列叫做偶排列。
• n阶行列式的定义：设有n²个数，排成n行n列的数表：

  a11	a12	...	a1n
  a21	a22	...	a2n
  ...	...	...	...
  an1	an2	...	ann

  做出表中位于不同行不同列的n个数的乘积，并冠以符号（-1）^t ，得到形如：（-1）ta_1p1a_2p2...anpn的项，其中p₁p₂...p_n为自然数1，2，...，n的一个排列，t为这个排列的逆序数，由于这样的排列共有n！个，因而形如这样的项共有n！项，所有这n！项代数和为：Σ(-1)^ta_1p1a_2p2...a_{npn。 称为n阶行列式。}
• 对角行列式的性质：

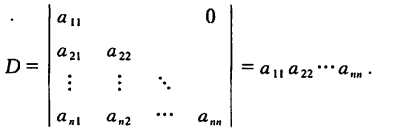
• 行列式对换的性质：

 

 

定理一 ：一个排列中的任意两个元素对换没排列改变奇偶性

推论： 奇排列变成标准排列的对换次数为奇数，偶排列变成标准排列的对换次数为偶数。

• 行列式的性质：

性质1：行列式和它的转置行列式相等。

性质2：互换行列式的两行（列），行列式变号。

性质3：如果横列式有两行（列）完全相同，则此行列式等于零。

性质4：行列式的某一行（列）中所有的元素都乘以同一数k，等于用数k乘以此行列式

性质5：行列式中如果有两行（列）的成比例，则此行列式等于0.

性质6：若行列式的某一列（行）的元素都是两数之和，则此行列式等于两个行列式之和。

性质7：把行里是的某一列（行）的各元素乘以同一数然后加到另一列（行）对应的元素上去，行列式不变。