树（数据结构二）

Posted 2020-11-24 anhaogoon

一、树

在实际使用时会根据链表和有序数组等数据结构的不同优势进行选择。有序数组的优势在于二分查找，链表的优势在于数据项的插入和数据项的删除。但是在有序数组中插入数据就会很慢，同样在链表中查找数据项效率就很低。综合以上情况，二叉树可以利用链表和有序数组的优势，同时可以合并有序数组和链表的优势，二叉树也是一种常用的数据结构。

 

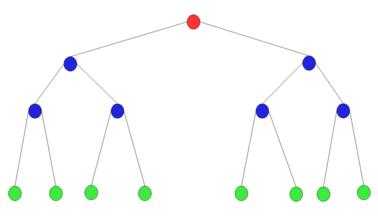
1、基本术语有：

若一个结点有子树，那么该结点称为子树根的“双亲”，子树的根称为该结点的“孩子”。有相同双亲的结点互为“兄弟”。一个结点的所有子树上的任何结点都是该结点的后裔。从根结点到某个结点的路径上的所有结点都是该结点的祖先。

 

结点的度：结点拥有的子树的数目

叶子结点：度为0的结点

分支结点：度不为0的结点

树的度：树中结点的最大的度

层次：根结点的层次为1，其余结点的层次等于该结点的双亲结点的层次加1

树的高度：树中结点的最大层次

森林：0个或多个不相交的树组成。对森林加上一个根，森林即成为树；删去根，树即成为森林。

 

2、特点：

树具有的特点有：

（1）每个结点有零个或多个子结点

（2）没有父节点的结点称为根节点

（3）每一个非根结点有且只有一个父节点

（4）除了根结点外，每个子结点可以分为多个不相交的子树。

 

3、二叉树的性质

性质1：二叉树第i层上的结点数目最多为2^i-1(i>=1)

性质2：深度为k的二叉树至多有2^k-1个结点（k>=1）

性质3：包含n个结点的二叉树的高度至少为(log₂n)+1

性质4：在任意一棵二叉树中，若终端结点的个数为n₀，度为2的结点数为n₂，则n₀=n₂+1

 证明：

n=n₀+n₁+n₂

m=n₁+2n2(一个叶子节点)

得出 n₀=n₂+1