0043数据结构之红黑树
Posted xiao1572662
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了0043数据结构之红黑树相关的知识,希望对你有一定的参考价值。
----------------------红黑树-----------------------------
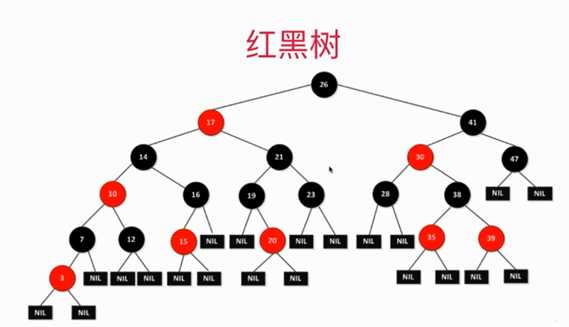
红黑树仍然是一颗二分搜索树,和AVL一样,都是在二分搜索树的基础上加了一些限制条件:具体的5个限制条件如下:
1) 每个节点或者是红色的,或者是黑色的
2) 根节点是黑色的
3) 每一个叶子节点(最后的空节点叫叶子节点)是黑色的
4) 如果有一个节点是红色的,那么它的两个孩子节点都是黑色的
5) 从任意一个节点到叶子节点,经过的黑色节点是一样的
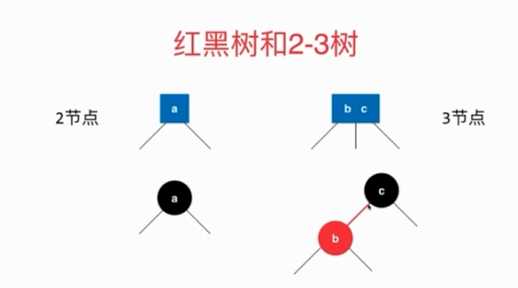
2-3树是一颗绝对平衡的树:从根节点到任意一个叶子节点经过的节点数是相同的,是通过融合(新加的节点一定是先和父亲节点融合,红黑树也是这个原理,所以红黑树新加的节点一定是红色的,即构造方法默认红色)-拆分-融合的形式来保证绝对平衡的。
红色的节点:代表他和它的父亲是融合在一起的,代表2-3树中的3节点
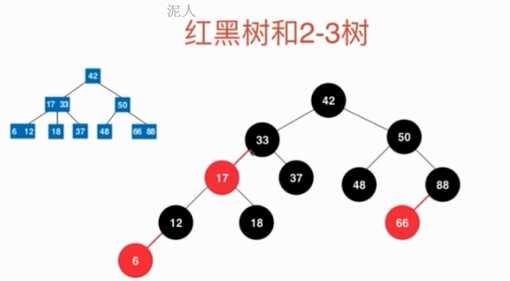
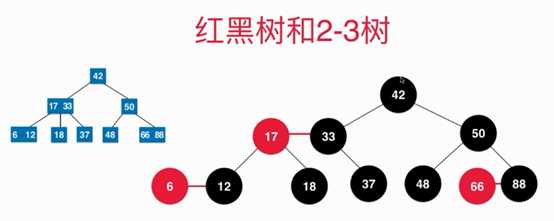
红黑树是“黑平衡”的二叉树:即红黑树限制条件的第5条,任意节点到叶子节点经过的黑色节点是相同的。 严格意思上来讲,不是平衡儿二叉树,即左右子树的高度差是有可能大于1的。红黑树最大高度2logn,所以时间复杂度是O(logn)的
红黑树与AVL树相比:
查找:红黑树略慢于AVL树
新增和删除:红黑树快于AVL树
所以如果存储的数据经常发生新增和删除:选择红黑树
如果存储的数据基本不发生变化,只是用于查询:选择AVL树
RBTree的代码实现如下(没有实现删除方法):
package rbTree;
import java.util.ArrayList;
public class RBTree<K extends Comparable<K>, V> {
private static final boolean RED = true;
private static final boolean BLACK = false;
private class Node{
public K key;
public V value;
public Node left, right;
public boolean color;
public Node(K key, V value){
this.key = key;
this.value = value;
left = null;
right = null;
color = RED;
}
}
private Node root;
private int size;
public RBTree(){
root = null;
size = 0;
}
public int getSize(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
// 判断节点node的颜色
private boolean isRed(Node node){
if(node == null)
return BLACK;
return node.color;
}
// node x
// / 左旋转 /
// T1 x ---------> node T3
// / /
// T2 T3 T1 T2
private Node leftRotate(Node node){
Node x = node.right;
// 左旋转
node.right = x.left;
x.left = node;
x.color = node.color;
node.color = RED;
return x;
}
// node x
// / 右旋转 /
// x T2 -------> y node
// / /
// y T1 T1 T2
private Node rightRotate(Node node){
Node x = node.left;
// 右旋转
node.left = x.right;
x.right = node;
x.color = node.color;
node.color = RED;
return x;
}
// 颜色翻转
private void flipColors(Node node){
node.color = RED;
node.left.color = BLACK;
node.right.color = BLACK;
}
// 向红黑树中添加新的元素(key, value)
public void add(K key, V value){
root = add(root, key, value);
root.color = BLACK; // 最终根节点为黑色节点
}
// 向以node为根的红黑树中插入元素(key, value),递归算法
// 返回插入新节点后红黑树的根
private Node add(Node node, K key, V value){
if(node == null){
size ++;
return new Node(key, value); // 默认插入红色节点
}
if(key.compareTo(node.key) < 0)
node.left = add(node.left, key, value);
else if(key.compareTo(node.key) > 0)
node.right = add(node.right, key, value);
else // key.compareTo(node.key) == 0
node.value = value;
if (isRed(node.right) && !isRed(node.left))
node = leftRotate(node);
if (isRed(node.left) && isRed(node.left.left))
node = rightRotate(node);
if (isRed(node.left) && isRed(node.right))
flipColors(node);
return node;
}
// 返回以node为根节点的二分搜索树中,key所在的节点
private Node getNode(Node node, K key){
if(node == null)
return null;
if(key.equals(node.key))
return node;
else if(key.compareTo(node.key) < 0)
return getNode(node.left, key);
else // if(key.compareTo(node.key) > 0)
return getNode(node.right, key);
}
public boolean contains(K key){
return getNode(root, key) != null;
}
public V get(K key){
Node node = getNode(root, key);
return node == null ? null : node.value;
}
public void set(K key, V newValue){
Node node = getNode(root, key);
if(node == null)
throw new IllegalArgumentException(key + " doesn‘t exist!");
node.value = newValue;
}
// 返回以node为根的二分搜索树的最小值所在的节点
private Node minimum(Node node){
if(node.left == null)
return node;
return minimum(node.left);
}
}
总结:
1) 二分搜索树适合处理完全随机的数据;不适用于处理近乎有序的数据,这样会退化为链表
2) AVL与红黑树相比,AVL更适合处理查询数据
3) 红黑树牺牲了平衡性,即有可能是不平衡的,但一定是“绝对黑平衡”的,2logn的高度,统计性能更优(即更适合增删改查的综合性操作)
以上是关于0043数据结构之红黑树的主要内容,如果未能解决你的问题,请参考以下文章