平均值μ；方差σ2；标准差σ

Posted 2020-11-24 tamkery

目录

• 1.平均值(mu)；方差(sigma^2)；标准差(sigma)数学公式
  • 平均数(又叫数学期望)
  • 方差和标准差
• 2.案例计算——以Matlab为工具
  • 计算平均数：
  • 计算标准差和方差
• 3.信息提取
  • 平均数
  • 标准差

1.平均值(mu)；方差(sigma^2)；标准差(sigma)数学公式

平均数(又叫数学期望)

对于数据:
[x_1 x_2 x_3 x_4cdots x_n]

平均数：

[mu= frac{1}{n}cdot sum_{i=1}^{n}{x_i}]
语言解释：平均数就是所有数加起来的和除以数据个数n。
数学的含义是：数据中间位置的具体数值。

方差和标准差

详细说明方差方差和标准差之前，先复习一下关于勾股定理（在西方又称毕达哥拉斯定理）和平面两点间距离公式。
在直角三角形中，对于边长a，b，c有如下关系：
[c^2=a^2+b^2]
即(c=sqrt{a^2+b^2 };a=sqrt{c^2 -b^2 })

在平面坐标系x-o-y下对任意两点(P(x_1,y_1)Q(x_2,y_2))间的距离D有:
[D=sqrt{(x_1-x_2)^2-(y_1-y_2)^2}]

通过勾股定理和平面两点间距离公式可以看出，型如(a=sqrt{c^2 -b^2 })
(D=sqrt{(x_1-x_2)^2-(y_1-y_2)^2})表示的含义为两个之间的距离。数值越小，证明两个之间越近。

一组数据，平均数是这个数据的中心，那么就可以用其他数据到平均数的距离来衡量数据和平均数的远近关系。即这组数据是聚拢一些呢，还是分散一些呢。
方差(sigma^2)
[sigma^2=frac{ 1 }{ n} cdot { sum_{i=1}^n (x_i-mu)^2 }]

因为距离D是需要开方的，所以方差的含义是距离的平方。对开方后的方差称为标准差(sigma)。
[sigma=sqrt{sigma^2}=sqrt{ frac{ 1 }{ n} cdot { sum_{i=1}^n (x_i-mu)^2 } }]

2.案例计算——以Matlab为工具

假设有两组数据：
[A=-3 ;-2; -1; 0; 1; 2; 3]
[B=-6; -4; -2; 0; 2; 4; 6 ]

计算平均数：

[mu_A=0]
[mu_B=0]

计算标准差和方差

[sigma_A=2.1602 ;sigma_A^2=4.6667 ]
[sigma_B=4.3205;sigma_B^2=18.667]

>>  A=[-3 -2 -1 0 1 2 3];
>> B=[-6 -4 -2 0 2 4 6];
#计算平均值
>> mean(A)
ans = 0
>> mean(B)
ans = 0
#计算标准差
>> ua=std(A)
ua =  2.1602
>> ub=std(B)
ub =  4.3205
#计算方差
>> ua**2
ans =  4.6667
>> ub**2
ans =  18.667

3.信息提取

平均数

[mu_A=mu_B=0]
说明两组数据的中间值数值一样，且都为零。平均值可以谅解为此数组中的中心位置。

标准差

[sigma_A=2.1602 ;sigma_A^2=4.6667 ]
[sigma_B=4.3205;sigma_B^2=18.667]
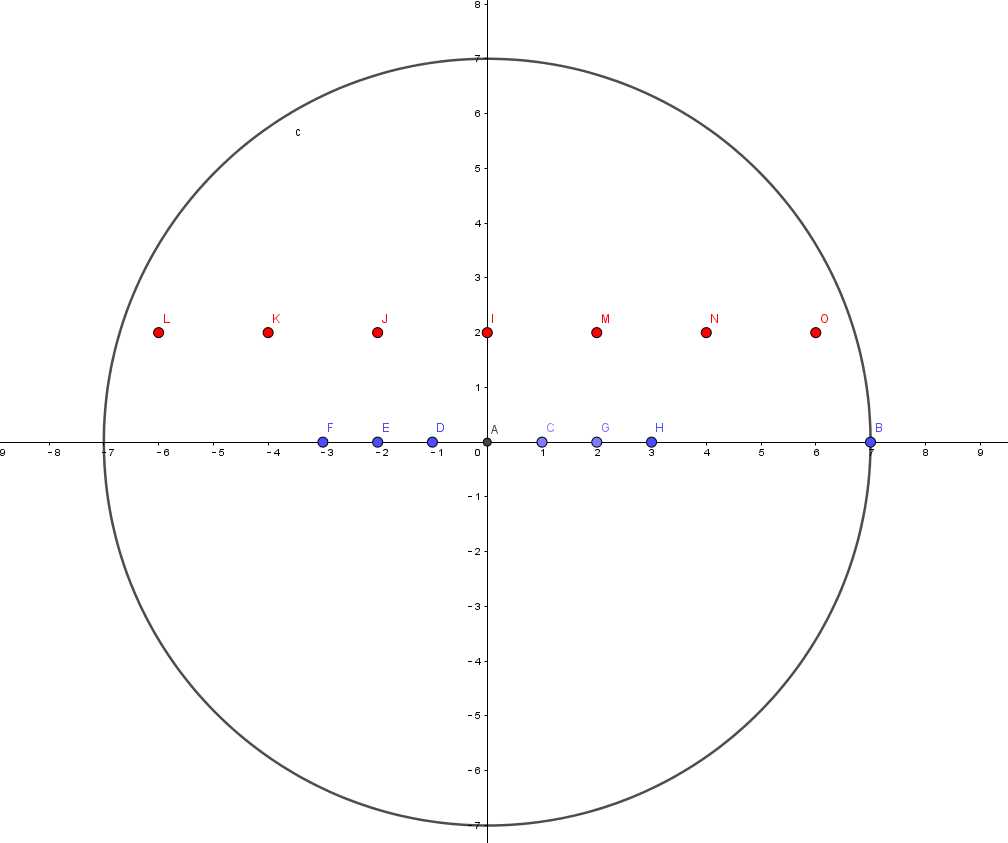
即(sigma_A<sigma_B)说明：
A组数据之间的距离较小，数据较聚拢；
B组数据之间的距离较大，数据较分散；