数据分析 第五篇：离群点检测

Posted 2020-11-23 ljhdo

离群点（outlier）是指和其他观测点偏离非常大的数据点，离群点是异常的数据点，但是不一定是错误的数据点。确定离群点对于数据分析会带来不利的影响，比如，增大错误方差、影响预测和影响正态性。

从散点图上可以直观地看到离群点，离群点是孤立的一个数据点；从分布上来看，离群点远离数据集中其他数据点。

 

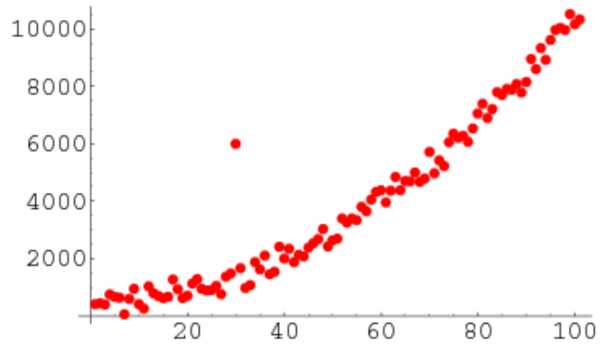
在数据处理过程中，检测离断点的方法，通常有Z-score 和 IQR。

一，Z-score方法

Z-score以标准差为单位去度量某一原始分数偏离平均数的距离，它回答了一个问题："一个给定分数距离平均数多少个标准差?"，Z-score的公式是：

Z-score = (Observation — Mean)/Standard Deviation
z = (X — μ) / σ

使用Python来实现，通常把远离标准差3倍距离以上的数据点视为离群点，也就是说，把Z-score大于3的数据点视作离群点：

import numpy as np
import pandas as pd

def detect_outliers(data,threshold=3):
    mean_d = np.mean(data)
    std_d = np.std(data)
    outliers = []
    
    for y in data_d:
        z_score= (y - mean_d)/std_d 
        if np.abs(z_score) > threshold:
            outliers.append(y)
    return outliers

二，IQR方法

四分位点内距（Inter-Quartile Range，IQR），是指在第75个百分点与第25个百分点的差值，或者说，上、下四分位数之间的差，计算IQR的公式是：

IQR = Q3 − Q1 

IQR是统计分散程度的一个度量，分散程度通过需要借助箱线图来观察，通常把小于 Q1 - 1.5 * IQR 或者大于 Q3 + 1.5 * IQR的数据点视作离群点，探测离群点的公式是：

outliers =  value < ( Q1 - 1.5 * IQR )  or value > ( Q3 + 1.5 * IQR )

这种探测离群点的方法，是箱线图默认的方法，箱线图提供了识别异常值/离群点的一个标准：

异常值通常被定义为小于 Q_L - l.5 IQR 或者 大于 Q_u + 1.5 IQR的值，Q_L称为下四分位数， Q_u称为上四分位数，IQR称为四分位数间距，是Q_u上四分位数和Q_L下四分位数之差，其间包括了全部观察值的一半。

箱线图的各个组成部分的名称及其位置如下图所示：

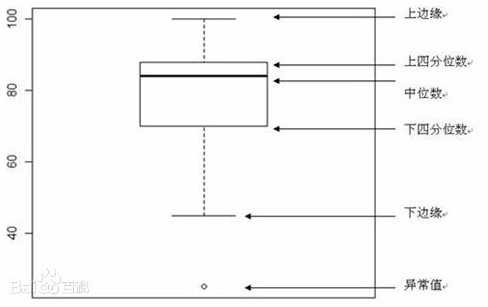
箱线图可以直观地看出数据集的以下重要特性：

• 中心位置：中位数所在的位置就是数据集的中心，从中心位置向上或向下看，可以看出数据的倾斜程度。
• 散布程度：箱线图分为多个区间，区间较短时，表示落在该区间的点较集中；
• 对称性：如果中位数位于箱子的中间位置，那么数据分布较为对称；如果极值离中位数的距离较大，那么表示数据分布倾斜。
• 离群点：离群点分布在箱线图的上下边缘之外。

使用Python实现，参数sr是Series类型的变量：

def detect_outliers(sr):
    q1 = sr.quantile(0.25)
    q3 = sr.quantile(0.75)
    iqr = q3-q1 #Interquartile range
    fence_low  = q1-1.5*iqr
    fence_high = q3+1.5*iqr
    outliers = sr.loc[(sr < fence_low) | (sr > fence_high)]
    return outliers

 

 

参考文档：