Matlab如何在解微分方程并将数值代入时使用parfor

Posted 2023-05-17

代码在运行时显示
错误使用 syms (line 212)
透明度违例错误。
请参阅有关透明度的 Parallel Computing Toolbox 文档
代码如下
function SRD=SRD(S,GD,Di,Ri)
% M=50; % 分层数
Di = Di*(10^12) /24;
Ri = Ri*(10^3) ;
c = Ri/Di ;

% 粒径读取自GD

n = size(GD) ;

SRD =zeros(50,n(2)) ;
SRA = sym(zeros(n(2),1));

parfor j = 1:1:n(2)
r_max = GD(j) ;
syms r SR(r) ;

SR1 = diff(SR) ;
SR2 = diff(SR,2) ;

SR = dsolve ( SR2==c-((2/r)*SR1) ,SR1(10^(-6))==0,SR(r_max)==S,r) ;

SRA(j) = SR ;
end

参考技术A

没看到你的代码，不好判断。

举个例子来说，下面的代码：

parfor ii=1:10
    xTemp = ii;
    out(ii) = xTemp;
end
disp(xTemp);

就会导致类似的错误，这是因为，parfor的循环顺序是不确定的，这一点和for循环不一样。

追问

代码就在问题描述里，求问关于这种问题该如何修改？

参考技术B 不太懂啊😄帮不了你

Matlab常微分方程数值解法

实验目的

用Matlab实现欧拉法、后退欧拉法、梯形方法和改进欧拉公式

实验要求

1. 给出欧拉法、后退欧拉法、梯形方法和改进欧拉公式算法

2. 用Matlab实现欧拉法、后退欧拉法、梯形方法和改进欧拉公式

实验内容

 实验步骤

　　（1）欧拉法算法，

　　

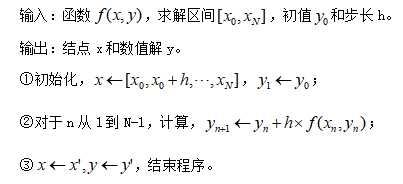
　　MATLAB实现，

 1 %数值解常微分方程欧拉算法
 2 %例子：dyfun=inline(‘y-2*x/y‘);[x,y]=euler2(dyfun,[0,1],1,0.2);
 3 %输入：函数dfun(x,y)，求解区间xspan[x0,xN]，初值y0，步长h
 4 %输出：节点x，数值解y
 5 function [x,y]=euler2(dyfun,xspan,y0,h)
 6 x=xspan(1):h:xspan(2);y(1)=y0;
 7 for n=1:length(x)-1
 8     y(n+1)=y(n)+h*feval(dyfun,x(n),y(n));
 9 end
10 x=x‘;y=y‘;
11 end

euler2

　　求解【题目】，

 （2）后退欧拉法算法，

　　MATLAB实现

 1 %数值解常微分后退欧拉法算法
 2 %例子：dfun=inline(‘x+y‘,‘x‘,‘y‘);[x,y]=eulerh1(dfun,0,1,0.02,5)
 3 %输入：函数dfun(x,y)，初值x0,y0,步长h,维度N
 4 %输出：结点x和数值解y
 5 function [x,y]=eulerh1(dfun,x0,y0,h,N)
 6 x=zeros(1,N+1);
 7 y=zeros(1,N+1);
 8 x(1)=x0;y(1)=y0;
 9 for n=1:N
10     x(n+1)=x(n)+h;
11     z0=y(n)+h*dfun(x(n),y(n));
12     for k=1:3
13         z1=y(n)+h*dfun(x(n+1),z0);
14         if abs(z1-z0)<1e-6
15             break;
16         end
17         z0=z1;
18     end
19     y(n+1)=z1;
20 end

eulerh1

　　求解【题目】，

　　

 （3）梯形方法算法，

 　　MATLAB实现，

 1 %数值解常微分梯形欧拉法算法
 2 %例子：dfun=inline(‘x+y‘,‘x‘,‘y‘);[x,y]=eulert(dfun,0,1,0.02,5)
 3 %输入：函数dfun(x,y)，初值x0,y0,步长h,维度N
 4 %输出：结点x和数值解y
 5 function [x,y]=eulert(dfun,x0,y0,h,N)
 6 x=zeros(1,N+1);
 7 y=zeros(1,N+1);
 8 x(1)=x0;y(1)=y0;
 9 for n=1:N
10     x(n+1)=x(n)+h;
11     z0=y(n)+h*dfun(x(n),y(n));
12     for k=1:3
13         z1=y(n)+(h/2)*(dfun(x(n),y(n))+dfun(x(n+1),z0));
14         if abs(z1-z0)<1e-6
15             break;
16         end
17         z0=z1;
18     end
19     y(n+1)=z1;
20 end

eulert

 　　求解【题目】，

 　　

（2）改进欧拉公式算法，

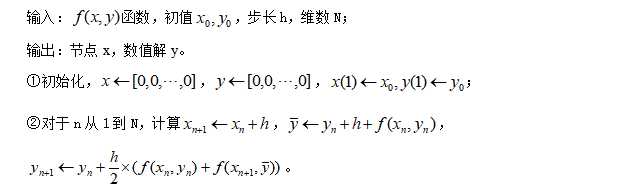
 　　MATLAB实现，

 1 %数值解常微分改进欧拉法算法
 2 %例子：dfun=inline(‘x+y‘,‘x‘,‘y‘);[x,y]=eulerh1(dfun,0,1,0.02,5)
 3 %输入：函数dfun(x,y)，初值x0,y0,步长h,维度N
 4 %输出：结点x和数值解y
 5 function [x,y]=eulerg2(dfun,x0,y0,h,N)
 6 x=zeros(1,N+1);
 7 y=zeros(1,N+1);
 8 x(1)=x0;y(1)=y0;
 9 for n=1:N
10     x(n+1)=x(n)+h;
11     ybar=y(n)+h*dfun(x(n),y(n));
12     y(n+1)=y(n)+(h/2)*(dfun(x(n),y(n))+dfun(x(n+1),ybar));
13 end
14 end

eulerg2

　　求解【题目】，

　　

求解结果，

　　

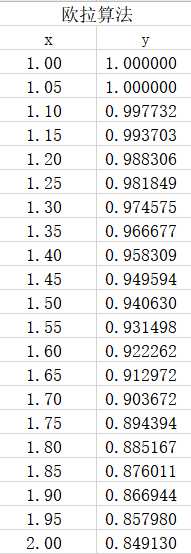
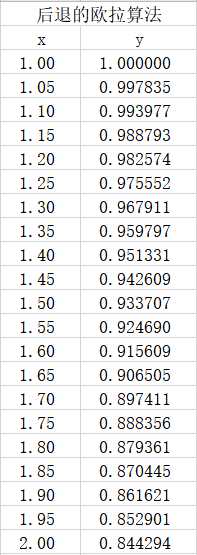
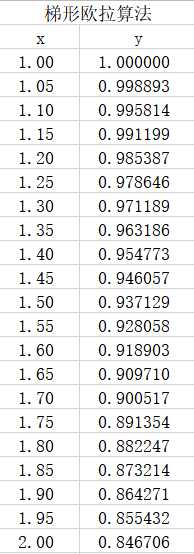
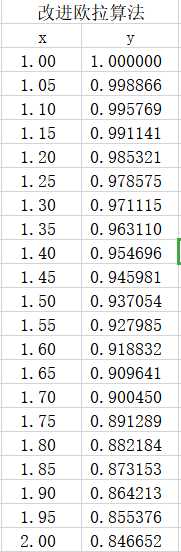
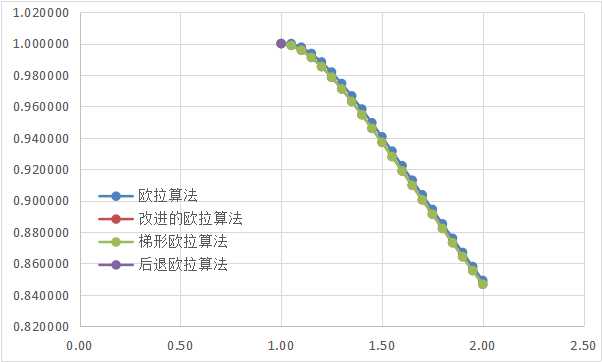
 小结

　　就给定的题目并没有体现出这些算法之间的差异。