原文转:http://users.rowan.edu/~polikar/WTpart1.html
五、终极解决方案:小波变换
小波变换是这样一种变换:它提供了信号的时频表示(还有一些变换可以提供这些信息,如短时傅立叶变化,魏格纳分布等等)。
在任一刻出现的特殊的频谱分量都有特殊的意义。这种情况下,如果知道了这些特殊的频谱分量出现的时间会比较有益。举例来说,在脑电图中,一个事件相关电位的潜伏期是主要关注点(事件相关电位是指大脑对某一特定刺激的反应,例如闪灯,这种反应的潜伏期是从刺激的开始到反应发生这段时间)。
小波变换可以同时提供时间和频率信息,因此给出了信号的一种时频表示。
但是小波变换到底是如何变换的仍然是一个不同的有趣故事,需要在理解了短时傅立叶变换(STFT)之后再解释。小波变换是被用来替代短时傅立叶变换(STFT)的。我们将在后面详细阐述STFT。现在可以说,一些在STFT中遇到的有关分辨率的问题,可以用小波变换解决。
为了长话短说,我们略过一些时域信号的高通和低通滤波处理,这些滤波器用来滤除信号中的低频和高频部分分量。这个过程是重复进行的,每一刻都可以从信号中滤除一些频率分量。
这里解释一下滤波过程是如何工作的:假定我们有一个信号,其中最高频分量为1000Hz。第一步,我们通过高通和低通滤波器把信号分成两部分(滤波器必须满足某些特定的条件,即允许条件),结果产生了同一信号的两个不同版本,0-500Hz的信号(低通)和500-1000Hz的信号(高通)。
然后,我们可以拿任意一部分(通常是低频部分)或者二者来做相同的处理。这个过程叫做分解。
假设我们拿低频部分做了处理,现在我们就有了3列数据,分别为0-250Hz,250-500Hz和500-1000Hz。
然后再对低通滤波过的信号做高通和低通滤波处理,现在我们就有了4列数据,分别为0-125Hz,125-250Hz,250-500Hz和500-1000Hz。我们持续进行这个处理过程,直到将信号分解到一个预定义的级别。这样我们就有了一系列信号,这些信号实际上表示相同的信号,但是每一个序列都有不同的频带。我们知道哪些信号对应哪个频段,如果我们将这些信号放在一起画出三维图,一个轴表示时间,频率在另外一个轴上,幅度在第三个轴上。这幅图会告诉我们在某时刻出现的是什么频率的信号(这里有一个问题,叫做“不确定性原理”,即我们不能确切的知道哪个频率出现在哪个时间点上,我们仅仅知道那个频段出现在哪个时间段内,后文中将有更多关于此的介绍)。
不过,我仍然想用一个简明扼要的方式解释它:
最初是由海森堡发现并阐述了不确定性原理(测不准原理),这个原理是这样的,移动粒子的动量和位置不能同时确定,对我们这个课题则是这样的:
在时频平面内的一个确切的点上,信号的频率和发生时间不能同时确定。换句话说:在任意一个时间点,我们不能确定哪个频谱分量存在。我们能做到的是在一个给定的时间段内确定哪个频谱分量存在。这是一个设计到分辨率的问题,正是因为这个原因,才使得研究者们从快速傅立叶变换(STFT)转到了小波变换(WT)上。快速傅立叶变换的分辨率是固定的,而小波变换则能给出不同的分辨率:
高频信号在时域内可以得到很好的解决,低频信号则可以在频域内得到很好的解决,这意味着,相对于低频分量,高频分量更容易在时域内定位(因为有更小的相对误差)。反而言之,低频分量更容易在频域内定位。看下面这张图:
f ^
|******************************************* continuous
|* * * * * * * * * * * * * * * wavelet transform
|* * * * * * *
|* * * *
|* *
--------------------------------------------> time
对上图的解释是:最上面一行是对高频信号的多个采样,其采样间隔时间也较短。就是说高频信号更容易在时域内处理。最下面的一行是对低频信号的采样,特征点较少,因此,低频信号在时域内并不容易处理。
^frequency
|
|
|
| *******************************************************
|
|
|
| * * * * * * * * * * * * * * * * * * * discrete time
| wavelet transform
| * * * * * * * * * *
|
| * * * * *
| * * *
|----------------------------------------------------------> time
在离散时间域内,信号的时间分辨率如上图所示,但是现在,频率信息的分辨率在每一个阶段都不相同。注意,低频信号更容易在频域内处理,高频则正好相反。注意到图中后续频率分量的间隔是如何随频率增高(这里应为降低)而增大的。
下图是一些连续小波变换的例子。让我们以一个正弦波为例,这个正弦波包含了出现在不同时刻的两个频率分量。前半部分是低频信号,后面是高频信号。

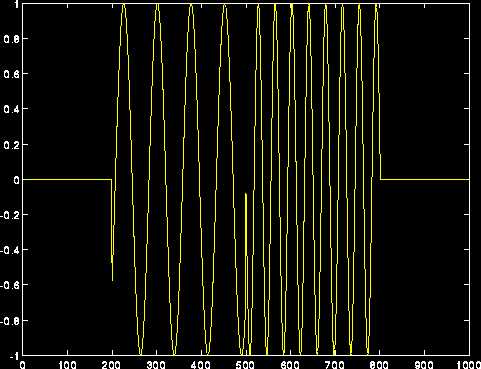
图1.10
对上图的连续小波变换如下:
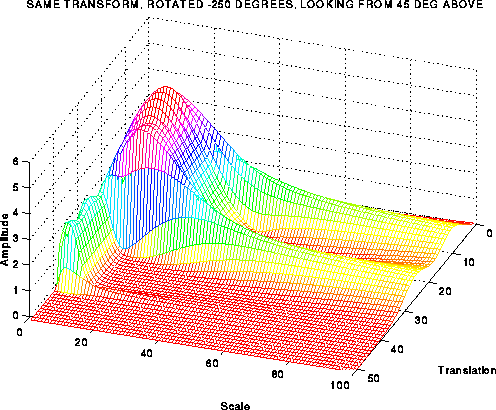
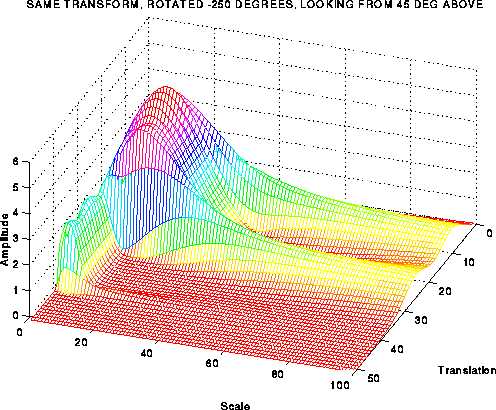
图1.11
注意到上图中,以“尺度”为标签的轴代表频率。“尺度”这个概念将会在后续章节进行阐述,但是这时需要注意的是尺度正好与频率成反比,即:尺度越大频率越低,尺度越小频率越高。因此,图中的小尖峰反映了信号中的高频分量,大的尖峰则反映了信号中的低频分量(在时域内低频信号是先出现的)。
你可能被图中的频率分辨率搞迷惑了,因为高频信号也得到了很好的频率分辨率。但是需要注意的是,高频信号的尺度分辨率很高,高尺度分辨率意味着低频率分辨率,反之则反。更多关于此的介绍在文章的后续部分。