点到平面的距离怎么计算?
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了点到平面的距离怎么计算?相关的知识,希望对你有一定的参考价值。
参考技术A点到平面距离公式是:
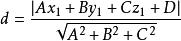
点到平面距离是指空间内一点到平面内一点的最小长度叫做点到平面的距离,特殊的有,当点在平面内,则点到平面的距离为0。
扩展资料:
点到平面的距离计算
向量法计算点到平面的距离就是把点和平面放在直角坐标系下,这样,点和平面的位置均可用坐标来表示,如图所示:
 点到平面的距离计算
点到平面的距离计算
平面π的方程为:Ax+By+Cz+D=0,向量

为平面的法向量,平面外一点
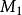
坐标为
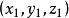
,在平面上取一点
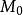
,则点

到平面π的距离为:
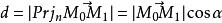
其中α为向量
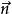
与

的夹角,


而

由于点
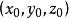
在平面π上,因此有

即

由此可得

所以,

此公式即为点到平面的距离公式。
参考资料来源:百度百科-点到平面距离
代数47 ----点到平面及直线的距离
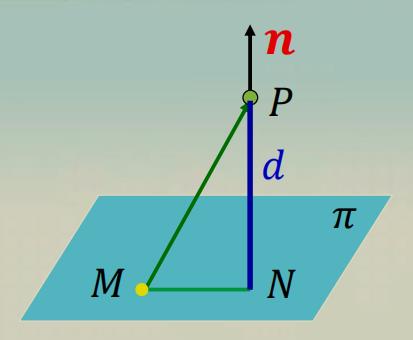
点到平面的距离
设平面
π
\\pi
π 的方程为
A
x
+
B
y
+
C
z
+
D
=
0
A x+B y+C z+D=0
Ax+By+Cz+D=0, 法向量为
n
=
(
A
,
B
,
C
)
n=(A, B, C)
n=(A,B,C).
取平面
π
\\pi
π 上的一点
M
(
x
1
,
y
1
,
z
1
)
M\\left(x_{1}, y_{1}, z_{1}\\right)
M(x1,y1,z1),
则点
P
(
x
0
,
y
0
,
z
0
)
P\\left(x_{0}, y_{0}, z_{0}\\right)
P(x0,y0,z0) 到平面
π
\\pi
π 的距离为
d
=
∣
(
M
P
→
)
n
∣
=
∣
M
P
→
⋅
n
∣
∣
n
∣
=
∣
A
(
x
0
−
x
1
)
+
B
(
y
0
−
y
1
)
+
C
(
z
0
−
z
1
)
∣
A
2
+
B
2
+
C
2
d=\\left|(\\overrightarrow{M P})_{n}\\right|=\\frac{|\\overrightarrow{M P} \\cdot \\boldsymbol{n}|}{|\\boldsymbol{n}|}=\\frac{\\left|A\\left(x_{0}-x_{1}\\right)+B\\left(y_{0}-y_{1}\\right)+C\\left(z_{0}-z_{1}\\right)\\right|}{\\sqrt{A^{2}+B^{2}+C^{2}}}
d=∣∣∣(MP)n∣∣∣=∣n∣∣MP⋅n∣=A2+B2+C2∣A(x0−x1)+B(y0−y1)+C(z0−z1)∣
又 A x 1 + B y 1 + C z 1 + D = 0 , A x_{1}+B y_{1}+C z_{1}+D=0, Ax1+By1+Cz1+D=0, 故 d = ∣ A x 0 + B y 0 + C z 0 + D ∣ A 2 + B 2 + C 2 \\quad d=\\frac{\\left|A x_{0}+B y_{0}+C z_{0}+D\\right|}{\\sqrt{A^{2}+B^{2}+C^{2}}} d=A2+B2+C2∣Ax0+By0+Cz0+D∣.
点到平面的距离
d
=
∣
A
x
0
+
B
y
0
+
C
z
0
+
D
∣
A
2
+
B
2
+
C
2
d=\\frac{\\left|A x_{0}+B y_{0}+C z_{0}+D\\right|}{\\sqrt{A^{2}+B^{2}+C^{2}}}
d=A2+B2+C2∣Ax0+By0+Cz0+D∣
【
注
】
\\Large\\color{violet}{【注】}
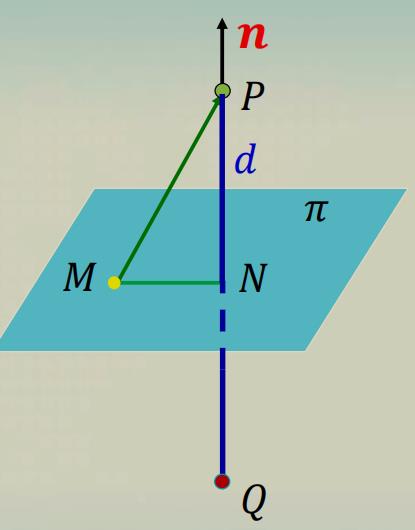
【注】可先求出垂足
N
N
N 的坐标, 再用两点距离公式求
d
=
∣
P
N
∣
d=|P N|
d=∣PN∣.
【
注
】
\\Large\\color{violet}{【注】}
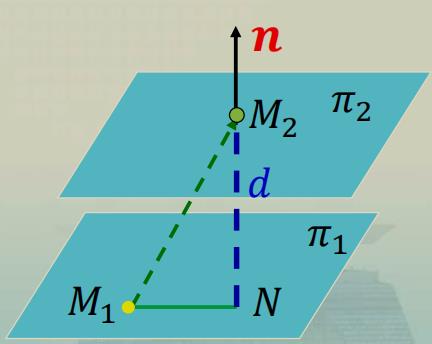
【注】两平行平面之间的距离归结为其中
一个平面上任一点到另一平面的距离.
例
1
\\Large\\color{violet}{例1}
例1 求点
P
(
1
,
3
,
2
)
P(1,3,2)
P(1,3,2) 到平面
π
:
2
x
−
y
−
2
z
−
1
=
0
\\pi: 2 x-y-2 z-1=0
π:2x−y−2z−1=0 的距离
d
d
d
并求点
P
P
P 关于平面
π
\\pi
π 的对称点
Q
Q
Q 的坐标.
【解】
(
1
)
\\quad(1)
(1) 由点到平面的距离公式知
d
=
∣
2
×
1
−
1
×
3
−
2
×
2
−
1
∣
2
2
+
(
−
1
)
2
+
(
−
2
)
2
=
2
d=\\frac{|2 \\times 1-1 \\times 3-2 \\times 2-1|}{\\sqrt{2^{2}+(-1)^{2}+(-2)^{2}}}=2
d=22+(−1)2+(−2)2以上是关于点到平面的距离怎么计算?的主要内容,如果未能解决你的问题,请参考以下文章