P4568 飞行路线分层图最短路

Posted 2020-11-23 yuanweidao

题目链接：https://www.luogu.org/problem/P4568

题目大意：给定n个点，m条无向边，k次机会经过边时代价为 0 。给出起点和终点，求其最短路径。

解题思路：

两种方法，一是用拆点分层，直接跑最短路。二是dis[][]开二维数组，表示已经用了 j 次免费机会时在 i 点的最短路径。

第一种方法数组需要多开大很多倍（因为拆点），当层数以及点比较多的时候，边也就非常多，代码跑起来很慢，在这里若不用优先队列dijsktra优化会超时。

第二种方法似乎更加好，不需要将一维数组开大很多倍，只需要用二维数组记录状态，然后更新即可。跑的边也会比较的少。代码更快。

对于第一种方法。图如下：

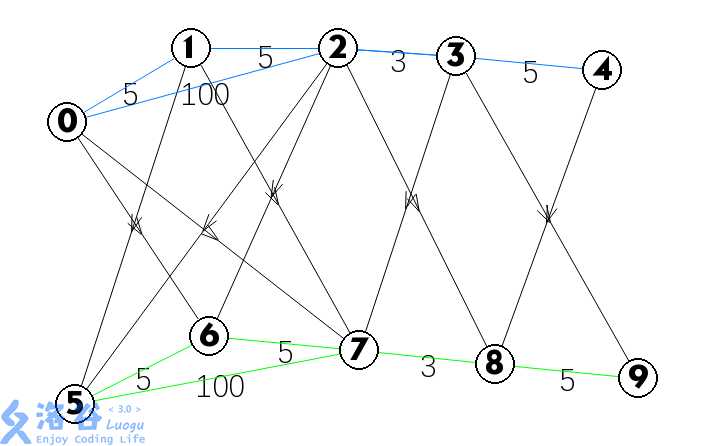
 1 #include<stdio.h>
 2 #include<string.h>
 3 #include<queue>
 4 #include<algorithm>
 5 #define mem(a, b) memset(a, b, sizeof(a))
 6 typedef long long ll;
 7 const int MAXN = 1e6 + 100;//建了多层 点成倍增加 
 8 const int MAXM = 5e6 + 100;
 9 const int inf = 0x3f3f3f3f;
10 using namespace std;
11 
12 int n, m, k, st, ed;
13 int head[MAXN], cnt;
14 int vis[MAXN];
15 ll dis[MAXN];  //距离开ll 稳 
16 
17 struct Edge
18 {
19     int to, next;
20     ll w;
21 }edge[MAXM];
22 
23 struct Node
24 {
25     int pot;
26     ll dis;
27     bool operator < (const Node &a)const
28     {
29         return dis > a.dis;
30     }
31 }node;
32 
33 void add(int a, int b, ll c)
34 {
35     cnt ++;
36     edge[cnt].to = b;
37     edge[cnt].w = c;
38     edge[cnt].next = head[a];
39     head[a] = cnt;
40 }
41 
42 void dij()
43 {
44     mem(dis, inf), mem(vis, 0);
45     priority_queue<Node> Q; //记得是优先队列 
46     while(!Q.empty())    Q.pop();
47     dis[st] = 0;
48     node.pot = st, node.dis = 0;
49     Q.push(node);
50     while(!Q.empty())
51     {
52         Node a = Q.top();//top()
53         Q.pop();
54         if(vis[a.pot])
55             continue;
56         vis[a.pot] = 1;
57         for(int i = head[a.pot]; i != -1; i = edge[i].next)
58         {
59             int to = edge[i].to;
60             if(vis[to]) //若该点以及确定了最短距离 则不需要再去比较了 
61                 continue;
62             if(dis[to] > dis[a.pot] + edge[i].w)
63             {
64                 dis[to] = dis[a.pot] + edge[i].w;
65                 node.pot = to, node.dis = dis[to];
66                 Q.push(node);
67             }
68         }
69     }
70 }
71 
72 int main()
73 {
74     cnt = 0, mem(head, -1);
75     scanf("%d%d%d", &n, &m, &k);
76     scanf("%d%d", &st, &ed);
77     for(int i = 1; i <= m; i ++)
78     {
79         int a, b;
80         ll c;
81         scanf("%d%d%lld", &a, &b, &c);
82         add(a, b, c);
83         add(b, a, c);
84         for(int j = 1; j <= k; j ++)
85         {
86             add(a + (j - 1) * n, b + j * n, 0);  //上一层往下一层建边权为 0 的边 
87             add(b + (j - 1) * n, a + j * n, 0);
88             add(a + j * n, b + j * n, c);  //每一层本身的边也要建 
89             add(b + j * n, a + j * n, c);
90         }
91     }
92     dij();
93     ll ans = inf;
94     for(int i = 0; i <= k; i ++)  //选择到终点距离最短的那一层答案 
95         ans = min(ans, dis[ed + i * n]);
96     printf("%lld
", ans);
97     return 0;
98 }

建图时分层

 1 #include<stdio.h>
 2 #include<string.h>
 3 #include<queue>
 4 #define mem(a, b) memset(a, b, sizeof(a))
 5 typedef long long ll;
 6 const int MAXN = 1e4 + 10;
 7 const int MAXM = 5e4 + 10;
 8 const int inf = 0x3f3f3f3f;
 9 using namespace std;
10 
11 int n, m, k, st, ed;
12 int head[MAXN], cnt, vis[MAXN][12];
13 ll dis[MAXN][12];
14 
15 struct Edge
16 {
17     int to, next;
18     ll w;
19 }edge[2 * MAXM];
20 
21 struct Node
22 {
23     int pot, num;  //点 以及 用了的机会次数 
24     ll dis;
25     bool operator < (const Node &a)const
26     {
27         return dis > a.dis;
28     }
29 }node;
30 
31 void add(int a, int b, ll c)
32 {
33     cnt ++;
34     edge[cnt].w = c;
35     edge[cnt].to = b;
36     edge[cnt].next = head[a];
37     head[a] = cnt;
38 }
39 
40 void dij()
41 {
42     mem(dis, inf), mem(vis, 0);
43     node.pot = st, node.dis = 0, node.num = 0;
44     dis[st][0] = 0;
45     priority_queue<Node> Q;
46     Q.push(node);
47     while(!Q.empty())
48     {
49         Node a = Q.top();
50         Q.pop();
51         if(vis[a.pot][a.num])
52             continue;
53         vis[a.pot][a.num] = 1;
54         for(int i = head[a.pot]; i != -1; i = edge[i].next)
55         {
56             int to = edge[i].to;
57             if(dis[to][a.num] > dis[a.pot][a.num] + edge[i].w) //不使用免费机会
58             {
59                 dis[to][a.num] = dis[a.pot][a.num] + edge[i].w;
60                 node.pot = to, node.dis = dis[to][a.num], node.num = a.num;
61                 Q.push(node);
62             }
63             if(a.num == k)   //如果已经把免费机会使用完了
64                 continue;
65             if(dis[to][a.num + 1] > dis[a.pot][a.num])
66             {
67                 dis[to][a.num + 1] = dis[a.pot][a.num];
68                 node.pot = to, node.dis = dis[to][a.num + 1], node.num = a.num + 1;
69                 Q.push(node);
70             }
71         }
72     }
73 }
74 
75 int main()
76 {
77     mem(head, -1), cnt = 0;
78     scanf("%d%d%d", &n, &m, &k);
79     scanf("%d%d", &st, &ed);
80     for(int i = 1; i <= m; i ++)
81     {
82         int a, b;
83         ll c;
84         scanf("%d%d%lld", &a, &b, &c);
85         add(a, b, c);
86         add(b, a, c);
87     }
88     dij();
89     ll ans = inf;
90     for(int i = 0; i <= k; i ++)
91         ans = min(ans, dis[ed][i]);
92     printf("%lld
", ans);
93     return 0;
94 }

二维数组