algo&ds2.线性表

Posted 2020-11-22 ericling

1.线性表

线性表（英语：Linear List）是由n（n≥0）个数据元素（结点）a[0]，a[1]，a[2]…，a[n-1]组成的有限序列。

其中：

• 数据元素的个数n定义为表的长度 = "list".length() （"list".length() = 0（表里没有一个元素）时称为空表）
• 将非空的线性表（n>=1）记作：（a[0]，a[1]，a[2]，…，a[n-1]）
• 数据元素a[i]（0≤i≤n-1）只是个抽象符号，其具体含义在不同情况下可以不同

一个数据元素可以由若干个数据项组成。数据元素称为记录，含有大量记录的线性表又称为文件。这种结构具有下列特点：存在一个唯一的没有前驱的（头）数据元素；存在一个唯一的没有后继的（尾）数据元素；此外，每一个数据元素均有一个直接前驱和一个直接后继数据元素。

2.线性表的存储结构

• 顺序表
• 链表
  • 单链表
    • 动态单链表
    • 静态单链表
  • 双链表
  • 循环链表
    • 单循环链表
    • 双循环链表
  • 静态链表

3.顺序表

利用数组的连续存储空间顺序存放线性表的各元素

3.1结构体定义

如果需要使用自定义的结构体来维护一个顺序表，通常来讲结构体的元素一般是一个固定大小的数组（可用长度足够大），以及当前数组存放的元素个数，也即数组的长度

typedef struct LNode *List;
struct LNode {
    ElementType Data[MAXSIZE];
    int Last;//记录顺序表的最后一个元素的下标
} ;
struct LNode L;
List PtrL;

访问结构体的成员

• 访问下标为 i 的元素：L.Data[i] 或 PtrL->Data[i]
• 线性表的长度：L.Last+1 或 PtrL->Last+1
• 指针变量PtrL还可以这样访问两个属性(*PtrL).Data[i]和(*PtrL).Last，不过这种访问方式并不常用

而一般来讲，为了简单，不会去维护这样一个结构体，(因为一旦维护了这个结构体，就需要去封装相应的函数，比如说常见的插入、删除、查找等操作)，而是直接类似下面这样

ElementType data[MaxSize];
int length;

定义一个足够大的数组，然后定义一个对应关联的变量来时刻维护数组的长度。

这两种定义方式没有什么区别，一种是把常用操作封装好，方便调用，另一种则是需要时刻自己维护对应的属性。因为顺序表的结构足够简单，所以不定义结构体也是可以的。

3.2顺序表的常见操作

为了方便，这一节内容记录的都是在定义的结构体基础上，封装的常见操作。

1.初始化

List MakeEmpty( ) {
    List PtrL;
    PtrL = (List )malloc( sizeof(struct LNode) );
    PtrL->Last = -1;
    return PtrL;
}

初始化的顺序表，长度为0，所以Last为-1

2.查找

int Find( ElementType X, List PtrL ) {
    int i = 0;
    while( i <= PtrL->Last && PtrL->Data[i]!= X )
        i++;
    if (i > PtrL->Last) return -1; /* 如果没找到，返回-1 */
    else return i; /* 找到后返回的是存储位置 */
}

查找操作比较简单，从顺序表的第一个元素（下标为0开始）开始遍历。

还有一种更加巧妙一点的实现方式，就是引入哨兵思想。

int Find( ElementType X, List PtrL ) {
    PtrL->Data[0] = x;//顺序表第一个元素就是哨兵，赋值为x
    int i = PtrL->Last;//从最后一个元素开始遍历
    while( PtrL->Data[i]!= X )
        i--;
    return i;
}

这样做的好处很明显，少了边界的判断，可以优化时间复杂度，编码也更加简单。

注意：这里把下标为0的元素设置为哨兵，则要求顺序表从下标为1开始存储。而且，函数如果没有找到，则一定返回i=0

3.插入

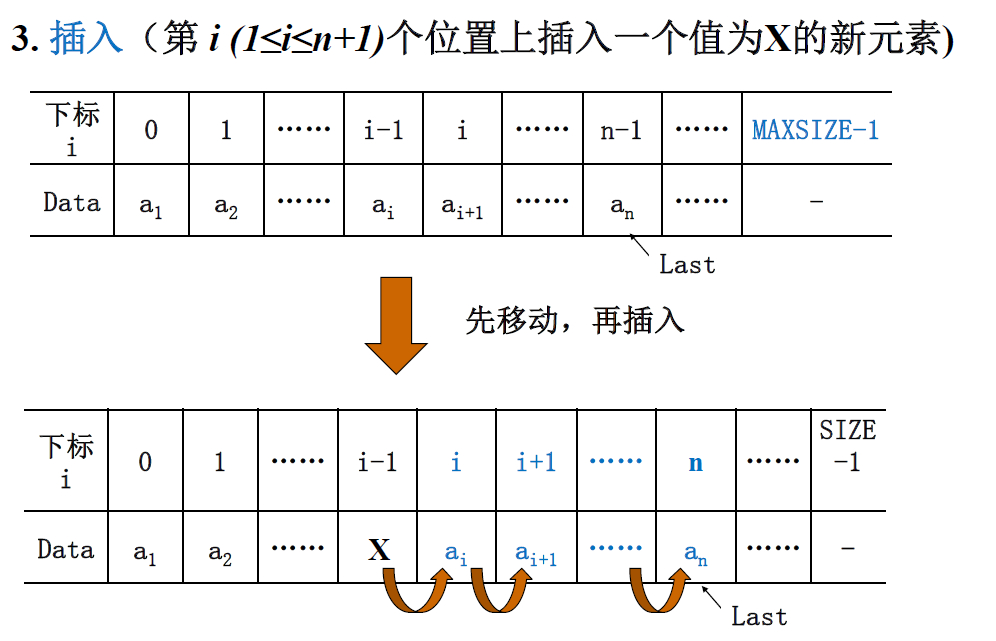
看图示应该要注意，移动的方向是从后往前移，如果从前往后移，则Data[i]=Data[i+1]=...=Data[n]，因为后面的元素都被前面移过来的元素给覆盖了。

void Insert( ElementType X, int i, List PtrL ) {
    int j;
    if ( PtrL->Last == MAXSIZE-1 ) { /* 表空间已满，不能插入*/
        printf(＂表满＂);
        return;
    }
    if ( i < 1 || i > PtrL->Last+2) { /*检查插入位置的合法性*/
        printf(＂位置不合法＂);
        return;
    }
    for ( j = PtrL->Last; j >= i-1; j-- )
        PtrL->Data[j+1] = PtrL->Data[j]; /*将 ai～ an倒序向后移动*/
    PtrL->Data[i-1] = X; /*新元素插入*/
    PtrL->Last++; /*Last仍指向最后元素*/
    return;
}

为什么这里需要判断顺序表的空间是否已满？

因为这个数组，是在初始化之后就固定了数组可容纳的元素个数MaxSize，一旦超出，则程序下标就会越界。C++提供了动态数组vector，可以很方便的支持动态扩展数组长度，而且基本的插入删除等操作都封装好了，可以很方便的使用。

4.删除

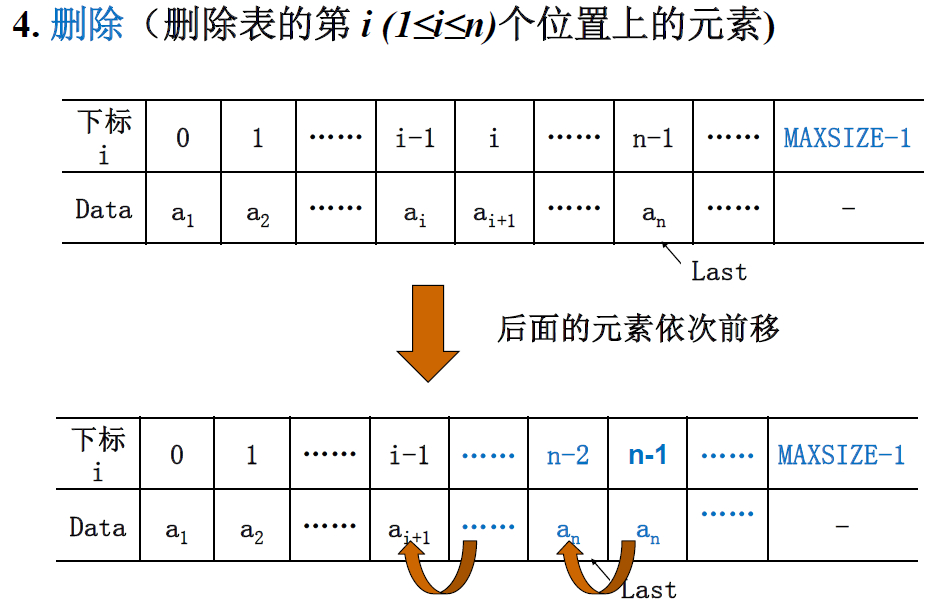
同样的，需要注意元素移动的方向，如果从后往前移，则最后面的元素会一直覆盖到Data[i]。

void Delete( int i, List PtrL ) {
    int j;
    if( i < 1 || i > PtrL->Last+1 ) { /*检查空表及删除位置的合法性*/
        printf (“不存在第%d个元素”, i );
        return ;
    }
    for ( j = i; j <= PtrL->Last; j++ )
        PtrL->Data[j-1] = PtrL->Data[j]; /*将 ai+1～ an顺序向前移动*/
    PtrL->Last--; /*Last仍指向最后元素*/
    return;
}

5.排序

因为排序算法比较多，本文不展开讲解，可以参考以下博文，内容包括了常见的十大排序算法的算法分析，时间复杂度和空间复杂度分析以及c实现和动图图解。

https://www.cnblogs.com/ericling/p/11877219.html

4.链表

不要求逻辑上相邻的两个元素物理上也相邻；通过“链”建立起数据元素之间的逻辑关系。插入、删除不需要移动数据元素，只需要修改“链”。

4.1单链表

typedef struct LNode *List;
struct LNode {
    ElementType Data;
    List Next;
};
struct Lnode L;
List PtrL;

1.求表长

int Length ( List PtrL ) {
    List p = PtrL; /* p指向表的第一个结点*/
    int j = 0;
    while ( p ) {
        p = p->Next;
        j++; /* 当前p指向的是第 j 个结点*/
    }
    return j;
}

时间复杂度O(n)

2.查找

按序查找

List FindKth( int K, List PtrL ) {
    List p = PtrL;
    int i = 1;
    while (p !=NULL && i < K ) {
        p = p->Next;
        i++;
    }
    if ( i == K ) return p;
    /* 找到第K个，返回指针 */
    else return NULL;
    /* 否则返回空 */
}

时间复杂度O(n)

按值查找

List Find( ElementType X, List PtrL ) {
    List p = PtrL;
    while ( p!=NULL && p->Data != X )
        p = p->Next;
    return p;
}

时间复杂度O(n)

3.插入

（1）先构造一个新结点，用s指向；
（2）再找到链表的第 i-1个结点，用p指向；
（3）然后修改指针，插入结点 ( p之后插入新结点是 s)

List Insert( ElementType X, int i, List PtrL ) {
    List p, s;
    if ( i == 1 ) { /* 新结点插入在表头 */
        s = (List)malloc(sizeof(struct LNode)); /*申请、填装结点*/
        s->Data = X;
        s->Next = PtrL;
        return s; /*返回新表头指针*/
    }
    p = FindKth( i-1, PtrL ); /* 查找第i-1个结点 */
    if ( p == NULL ) { /* 第i-1个不存在，不能插入 */
        printf("参数i错");
        return NULL;
    } else {
        s = (List)malloc(sizeof(struct LNode)); /*申请、填装结点*/
        s->Data = X;
        s->Next = p->Next; /*新结点插入在第i-1个结点的后面*/
        p->Next = s;
        return PtrL;
    }
}

4.删除

（1）先找到链表的第 i-1个结点，用p指向；
（2）再用指针s指向要被删除的结点（p的下一个结点）;
（3）然后修改指针，删除s所指结点;
（4）最后释放s所指结点的空间。

List Delete( int i, List PtrL ) {
    List p, s;
    if ( i == 1 ) { /* 若要删除的是表的第一个结点 */
        s = PtrL; /*s指向第1个结点*/
        if (PtrL!=NULL) PtrL = PtrL->Next; /*从链表中删除*/
        else return NULL;
        free(s); /*释放被删除结点 */
        return PtrL;
    }
    p = FindKth( i-1, PtrL ); /*查找第i-1个结点*/
    if ( p == NULL ) {
        printf("第%d个结点不存在", i-1);
        return NULL;
    } else if ( p->Next == NULL ) {
        printf("第%d个结点不存在", i);
        return NULL;
    } else {
        s = p->Next; /*s指向第i个结点*/
        p->Next = s->Next; /*从链表中删除*/
        free(s); /*释放被删除结点 */
        return PtrL;
    }
}

4.2双链表

双向链表，又称为双链表，是链表的一种，它的每个数据结点中都有两个指针，分别指向直接后继和直接前驱。所以，从双向链表中的任意一个结点开始，都可以很方便地访问它的前驱结点和后继结点。

typedef struct DuLNode {
    ElemType data;
    struct DuLNode *prior, *next;
} DuLNode, *DuLinkList;

4.3循环链表

4.3.1单循环链表

存储结构和单链表相同。

typedef struct LNode {
    ElemType data;
    struct LNode *next;
} LNode, *LinkList;

// 设立尾指针的单循环链表的12个基本操作
void InitList(LinkList *L) { // 操作结果：构造一个空的线性表L
    *L = (LinkList)malloc(sizeof(struct LNode)); // 产生头结点，并使L指向此头结点
    if (!*L) // 存储分配失败
        exit(OVERFLOW);
    (*L)->next = *L; // 指针域指向头结点
}

void DestroyList(LinkList *L) { // 操作结果：销毁线性表L
    LinkList q, p = (*L)->next; // p指向头结点
    while (p != *L) { // 没到表尾
        q = p->next;
        free(p);
        p = q;
    }
    free(*L);
    *L = NULL;
}

void ClearList(LinkList *L) /* 改变L */ { // 初始条件：线性表L已存在。操作结果：将L重置为空表
    LinkList p, q;
    *L = (*L)->next; // L指向头结点
    p = (*L)->next; // p指向第一个结点
    while (p != *L) { // 没到表尾
        q = p->next;
        free(p);
        p = q;
    }
    (*L)->next = *L; // 头结点指针域指向自身
}

Status ListEmpty(LinkList L) { // 初始条件：线性表L已存在。操作结果：若L为空表，则返回TRUE，否则返回FALSE
    if (L->next == L) // 空
        return TRUE;
    else
        return FALSE;
}

int ListLength(LinkList L) { // 初始条件：L已存在。操作结果：返回L中数据元素个数
    int i = 0;
    LinkList p = L->next; // p指向头结点
    while (p != L) { // 没到表尾
        i++;
        p = p->next;
    }
    return i;
}

Status GetElem(LinkList L, int i, ElemType *e) { // 当第i个元素存在时，其值赋给e并返回OK，否则返回ERROR
    int j = 1; // 初始化，j为计数器
    LinkList p = L->next->next; // p指向第一个结点
    if (i <= 0 || i > ListLength(L)) // 第i个元素不存在
        return ERROR;
    while (j < i) { // 顺指针向后查找，直到p指向第i个元素
        p = p->next;
        j++;
    }
    *e = p->data; // 取第i个元素
    return OK;
}

int LocateElem(LinkList L, ElemType e, Status(*compare)(ElemType, ElemType)) { // 初始条件：线性表L已存在，compare()是数据元素判定函数
    // 操作结果：返回L中第1个与e满足关系compare()的数据元素的位序。
    //           若这样的数据元素不存在，则返回值为0
    int i = 0;
    LinkList p = L->next->next; // p指向第一个结点
    while (p != L->next) {
        i++;
        if (compare(p->data, e)) // 满足关系
            return i;
        p = p->next;
    }
    return 0;
}

Status PriorElem(LinkList L, ElemType cur_e, ElemType *pre_e) { // 初始条件：线性表L已存在
    // 操作结果：若cur_e是L的数据元素，且不是第一个，则用pre_e返回它的前驱，
    //           否则操作失败，pre_e无定义
    LinkList q, p = L->next->next; // p指向第一个结点
    q = p->next;
    while (q != L->next) { // p没到表尾
        if (q->data == cur_e) {
            *pre_e = p->data;
            return TRUE;
        }
        p = q;
        q = q->next;
    }
    return FALSE; // 操作失败
}

Status NextElem(LinkList L, ElemType cur_e, ElemType *next_e) { // 初始条件：线性表L已存在
    // 操作结果：若cur_e是L的数据元素，且不是最后一个，则用next_e返回它的后继，
    //           否则操作失败，next_e无定义
    LinkList p = L->next->next; // p指向第一个结点
    while (p != L) { // p没到表尾
        if (p->data == cur_e) {
            *next_e = p->next->data;
            return TRUE;
        }
        p = p->next;
    }
    return FALSE; // 操作失败
}

Status ListInsert(LinkList *L, int i, ElemType e) /* 改变L */ { // 在L的第i个位置之前插入元素e
    LinkList p = (*L)->next, s; // p指向头结点
    int j = 0;
    if (i <= 0 || i > ListLength(*L) + 1) // 无法在第i个元素之前插入
        return ERROR;
    while (j < i - 1) { // 寻找第i-1个结点
        p = p->next;
        j++;
    }
    s = (LinkList)malloc(sizeof(struct LNode)); // 生成新结点
    s->data = e; // 插入L中
    s->next = p->next;
    p->next = s;
    if (p == *L) // 改变尾结点
        *L = s;
    return OK;
}

Status ListDelete(LinkList *L, int i, ElemType *e) /* 改变L */ { // 删除L的第i个元素，并由e返回其值
    LinkList p = (*L)->next, q; // p指向头结点
    int j = 0;
    if (i <= 0 || i > ListLength(*L)) // 第i个元素不存在
        return ERROR;
    while (j < i - 1) { // 寻找第i-1个结点
        p = p->next;
        j++;
    }
    q = p->next; // q指向待删除结点
    p->next = q->next;
    *e = q->data;
    if (*L == q) // 删除的是表尾元素
        *L = p;
    free(q); // 释放待删除结点
    return OK;
}

void ListTraverse(LinkList L, void(*vi)(ElemType)) { // 初始条件：L已存在。操作结果：依次对L的每个数据元素调用函数vi()
    LinkList p = L->next->next; // p指向首元结点
    while (p != L->next) { // p不指向头结点
        vi(p->data);
        p = p->next;
    }
    printf("
");
}

4.3.2双循环链表

// 线性表的双向链表存储结构
typedef struct DuLNode {
    ElemType data;
    struct DuLNode *prior, *next;
} DuLNode, *DuLinkList;

// 带头结点的双向循环链表的基本操作(14个)
void InitList(DuLinkList *L) {
    // 产生空的双向循环链表L
    *L = (DuLinkList)malloc(sizeof(DuLNode));
    if (*L)
        (*L)->next = (*L)->prior = *L;
    else
        exit(OVERFLOW);
}

void DestroyList(DuLinkList *L) {
    // 操作结果：销毁双向循环链表L
    DuLinkList q, p = (*L)->next; // p指向第一个结点
    while (p != *L) { // p没到表头
        q = p->next;
        free(p);
        p = q;
    }
    free(*L);
    *L = NULL;
}

void ClearList(DuLinkList L) { // 不改变L
    // 初始条件：L已存在。操作结果：将L重置为空表
    DuLinkList q, p = L->next; // p指向第一个结点
    while (p != L) { // p没到表头
        q = p->next;
        free(p);
        p = q;
    }
    L->next = L->prior = L; // 头结点的两个指针域均指向自身
}

Status ListEmpty(DuLinkList L) {
    // 初始条件：线性表L已存在。操作结果：若L为空表，则返回TRUE，否则返回FALSE
    if (L->next == L && L->prior == L)
        return TRUE;
    else
        return FALSE;
}

int ListLength(DuLinkList L) {
    // 初始条件：L已存在。操作结果：返回L中数据元素个数
    int i = 0;
    DuLinkList p = L->next; // p指向第一个结点
    while (p != L) { // p没到表头
        i++;
        p = p->next;
    }
    return i;
}

Status GetElem(DuLinkList L, int i, ElemType *e) {
    // 当第i个元素存在时，其值赋给e并返回OK，否则返回ERROR
    int j = 1; // j为计数器
    DuLinkList p = L->next; // p指向第一个结点
    while (p != L && j < i) { // 顺指针向后查找，直到p指向第i个元素或p指向头结点
        p = p->next;
        j++;
    }
    if (p == L || j > i) // 第i个元素不存在
        return ERROR;
    *e = p->data; // 取第i个元素
    return OK;
}

int LocateElem(DuLinkList L, ElemType e, Status(*compare)(ElemType, ElemType)) {
    // 初始条件：L已存在，compare()是数据元素判定函数
    // 操作结果：返回L中第1个与e满足关系compare()的数据元素的位序。
    // 若这样的数据元素不存在，则返回值为0
    int i = 0;
    DuLinkList p = L->next; // p指向第1个元素
    while (p != L) {
        i++;
        if (compare(p->data, e)) // 找到这样的数据元素
            return i;
        p = p->next;
    }
    return 0;
}

Status PriorElem(DuLinkList L, ElemType cur_e, ElemType *pre_e) {
    // 操作结果：若cur_e是L的数据元素，且不是第一个，则用pre_e返回它的前驱，
    // 否则操作失败，pre_e无定义
    DuLinkList p = L->next->next; // p指向第2个元素
    while (p != L) { // p没到表头
        if (p->data == cur_e) {
            *pre_e = p->prior->data;
            return TRUE;
        }
        p = p->next;
    }
    return FALSE;
}

Status NextElem(DuLinkList L, ElemType cur_e, ElemType *next_e) {
    // 操作结果：若cur_e是L的数据元素，且不是最后一个，则用next_e返回它的后继，
    // 否则操作失败，next_e无定义
    DuLinkList p = L->next->next; // p指向第2个元素
    while (p != L) { // p没到表头
        if (p->prior->data == cur_e) {
            *next_e = p->data;
            return TRUE;
        }
        p = p->next;
    }
    return FALSE;
}

DuLinkList GetElemP(DuLinkList L, int i) { // 另加
    // 在双向链表L中返回第i个元素的地址。i为0，返回头结点的地址。若第i个元素不存在，
    // 返回NULL
    int j;
    DuLinkList p = L; // p指向头结点
    if (i < 0 || i > ListLength(L)) // i值不合法
        return NULL;
    for (j = 1; j <= i; j++)
        p = p->next;
    return p;
}

Status ListInsert(DuLinkList L, int i, ElemType e) {
    // 在带头结点的双链循环线性表L中第i个位置之前插入元素e，i的合法值为1≤i≤表长+1
    // 改进算法2.18，否则无法在第表长+1个结点之前插入元素
    DuLinkList p, s;
    if (i < 1 || i > ListLength(L) + 1) // i值不合法
        return ERROR;
    p = GetElemP(L, i - 1); // 在L中确定第i个元素前驱的位置指针p
    if (!p) // p=NULL,即第i个元素的前驱不存在(设头结点为第1个元素的前驱)
        return ERROR;
    s = (DuLinkList)malloc(sizeof(DuLNode));
    if (!s)
        return OVERFLOW;
    s->data = e;
    s->prior = p; // 在第i-1个元素之后插入
    s->next = p->next;
    p->next->prior = s;
    p->next = s;
    return OK;
}

Status ListDelete(DuLinkList L, int i, ElemType *e) {
    // 删除带头结点的双链循环线性表L的第i个元素，i的合法值为1≤i≤表长
    DuLinkList p;
    if (i < 1) // i值不合法
        return ERROR;
    p = GetElemP(L, i); // 在L中确定第i个元素的位置指针p
    if (!p) // p = NULL,即第i个元素不存在
        return ERROR;
    *e = p->data;
    p->prior->next = p->next; // 此处并没有考虑链表头，链表尾
    p->next->prior = p->prior;
    free(p);
    return OK;
}

void ListTraverse(DuLinkList L, void(*visit)(ElemType)) {
    // 由双链循环线性表L的头结点出发，正序对每个数据元素调用函数visit()
    DuLinkList p = L->next; // p指向头结点
    while (p != L) {
        visit(p->data);
        p = p->next;
    }
    printf("
");
}

void ListTraverseBack(DuLinkList L, void(*visit)(ElemType)) {
    // 由双链循环线性表L的头结点出发，逆序对每个数据元素调用函数visit()
    DuLinkList p = L->prior; // p指向尾结点
    while (p != L) {
        visit(p->data);
        p = p->prior;
    }
    printf("
");
}

4.4静态链表

前面讲解的都是动态链表，即需要指针来建立结点之间的连接关系。而对有些问题来说结点的地址是比较小的整数（例如5位数的地址），这样就没有必要去建立动态链表，而应使用方便得多的静态链表。
静态链表的实现原理是hash，即通过建立一个结构体数组，并令数组的下标直接表示结点的地址，来达到直接访问数组中的元素就能访问结点的效果。另外，由于结点的访问非常方便，因此静态链表是不需要头结点的。静态链表结点定义的方法如下：

struct Node{
    typename data;//数据域
    int next;//指针域
}node[size];

参考资料：

• 《数据结构和算法》——中国大学MOOC，浙江大学，陈越、何钦铭
• https://zh.wikipedia.org/wiki/%E7%BA%BF%E6%80%A7%E8%A1%A8
• https://zh.wikipedia.org/wiki/%E5%8F%8C%E5%90%91%E9%93%BE%E8%A1%A8
• 《算法笔记》
• 《数据结构和算法》-极客时间专栏