二叉树的树形结构打印

Posted 2020-11-22 evenleee

打印树形结构初衷

树形结构是算法里很常见的一种数据结构，从二叉树到多叉树，还有很多变种。每当需要程序员自己手动实现树形结构时，因为结构本身的复杂性，不容易调试验证。但一般的调试对树形数据结构的整体把控十分有限，甚至会让人迷失在一大堆的调试信息海洋里。如果能够将数据树形打印出来，那么我们理解树形结构的算法就事半功倍。

树形打印方式

我们知道 Linux 有个 tree 命令用来打印树状目录列表，可以将某个目录下的所有文件和子目录一览无遗，非常直观，本文可以说就是为了实现这个效果，并给出源码实现。

树形打印可分为深度优先和广度优先两种。虽然广度优先更加直观，但基于我们的屏幕宽度不够，难以容纳整棵树，所以采用深度优先的方式。并且先打印右子树再打印左子树，测着头观察数据更加直观，哈哈！

#ifndef _AVLTREE_H
#define _AVLTREE_H

#include <iostream>

template<typename T>
class avlnode {
public:
    T val;
    avlnode* left;
    avlnode* right;
    avlnode(T x) :val(x), left(nullptr), right(nullptr) {}
};

template<typename T>
class avltree {
    typedef avlnode<T> avlnode;

public:
    avltree() : avlroot(nullptr) {}
    ~avltree() {}

    void insert(const T& val) { treeInsert(avlroot, val); }
    void del(const T& val) { treeDelete(avlroot, val); }
    void watch() { printTreeForWatch(avlroot); }

private:
    int max(int a, int b) { return a > b ? a : b; }
    int treeHeight(const avlnode* root) {
        if (root == nullptr)
            return 0;
        return max(treeHeight(root->left), treeHeight(root->right)) + 1;
    }
    int treeBalanceFector(const avlnode* root) {  //计算平衡因子
        if (root == nullptr)
            return 0;
        return treeHeight(root->left) - treeHeight(root->right);
    }
    avlnode* rotateLeft(avlnode* root) {
        avlnode* tmp = root->right;
        root->right = tmp->left;
        tmp->left = root;
        return tmp;
    }
    avlnode* rotateRight(avlnode* &root) {
        avlnode* tmp = root->left;
        root->left = tmp->right;
        tmp->right = root;
        return tmp;
    }
    avlnode* minNode(avlnode* root) {
        if (root->left != nullptr)
            root = root->left;
        return root;
    }
    avlnode* treeRebalance(avlnode* root) {
        int fector = treeBalanceFector(root);
        if (fector > 1 && treeBalanceFector(root->left) > 0)  // LL
            return rotateRight(root);
        if (fector > 1 && treeBalanceFector(root->left) <= 0) // LR
        {
            root->left = rotateLeft(root->left);
            return rotateRight(root);
        }
        if (fector < -1 && treeBalanceFector(root->right) <= 0) // RR
            return rotateLeft(root);
        if (fector < -1 && treeBalanceFector(root->right) > 0)  // RL
        {
            root->right = rotateRight(root->right);
            return rotateLeft(root);
        }
        return root;
    }
    void treeInsert(avlnode*& root, const T& val) {
        if (root == nullptr) {
            root = new avlnode(val);
        } else {
            if (val == root->val)
                return;
            if (val < root->val)
                treeInsert(root->left, val);
            else
                treeInsert(root->right, val);
        }
        root = treeRebalance(root);
    }
    void treeDelete(avlnode*& root, const T& val) {
        if (root == nullptr)
            return;

        if (val == root->val) {
            if (root->right != nullptr){
                avlnode* min_node = minNode(root->right);
                root->val = min_node->val;
                delete min_node;
            } else {
                avlnode* deleteNode = root;
                root = root->left;
                delete deleteNode;
            }
        } else {
            if (val < root->val)
                treeDelete(root->left, val);
            else
                treeDelete(root->right, val);
        }

        root = treeRebalance(root);
    }

    struct backlog {
        avlnode *node;
        int next_sub_idx;
    };

    enum { 
        LeftIndex,
        RightIndex
    };
    enum { MaxLevel = 64 };

    static inline void
    nbl_push(backlog *nbl, backlog **top, backlog **bottom) {
        if (*top - *bottom < MaxLevel) {
            (*(*top)++) = *nbl;
        }
    }
    static inline backlog *
    nbl_pop(backlog **top, backlog **bottom) {
       return *top > *bottom ? --*top : nullptr;
    }
    static inline int
    nbl_is_empty(backlog *top, backlog *bottom) {
        return top == bottom;
    }
    static inline bool 
    is_leaf(avlnode *node) {
        return node->left == nullptr && node->right == nullptr;
    }
    static void
    node_print(avlnode *node) {
        if (node != nullptr) {
            printf("%d
", node->val);
        }
    }
        
    static void printTreeForWatch(avlnode *root) {
        int level = 0;
        avlnode *node = root;
        backlog nbl;
        backlog *p_nbl = nullptr;
        backlog *top, *bottom, nblStack[MaxLevel];
        top = bottom = nblStack;

        for (;;) {
            if (node != nullptr) {
                //以下两句非常巧妙实现，回到回溯点时不打印回溯点，打印左节点，该过程循环两遍，
                //第一遍不打印，第二遍节点存在，且p_nbl已为空，此时sub_index为RightIndex，会打印
                int sub_index = p_nbl != nullptr ? p_nbl->next_sub_idx : RightIndex;
                p_nbl = nullptr;   
                
                //记录回溯点，先保存左再保存右，当前sub_index为RightIndex打印
                if (is_leaf(node) || sub_index == LeftIndex) {  
                    nbl.node = nullptr;                    
                    nbl.next_sub_idx = RightIndex;
                } else {
                    nbl.node = node;
                    nbl.next_sub_idx = LeftIndex; 
                }
                nbl_push(&nbl, &top, &bottom);
                level++;
                if (sub_index == RightIndex) {
                    for (int i = 1; i < level; ++i) {
                        if (i == level - 1) {
                            printf("%-8s", "+-------");
                        } else {
                            if (nblStack[i - 1].node != nullptr) {
                                printf("%-8s", "|");
                            } else {
                                printf("%-8s", " ");
                            }
                        }
                    }
                    node_print(node);
                }
                node = sub_index == LeftIndex ? node->left : node->right;
            } else {
                p_nbl = nbl_pop(&top, &bottom);
                if (p_nbl == nullptr) {
                    break;
                }
                node = p_nbl->node;
                level--;
            }
        }
    }

private: 
    avlnode* avlroot;
};

#endif 

测试验证如下：

int main() {
  avltree<int> tree;
  for (int i = 0; i < 10; ++i) {
    tree.insert(i);
  }
  tree.watch();

  system("pause");
  return 0;
}

结果：

 

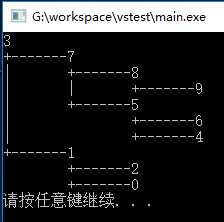
参考文章：https://www.v2ex.com/t/338653