机器学习模型可解释的重要及必要性

Posted 2023-05-12

机器学习模型可解释的重要及必要性不管你是管理自己的资金还是客户资金，只要你在做资产管理，每一步的投资决策都意义重大，做技术分析或基

参考技术A 机器学习模型可解释的重要及必要性
不管你是管理自己的资金还是客户资金，只要你在做资产管理，每一步的投资决策都意义重大，做技术分析或基本面分析的朋友很清楚地知道每一个决策的细节，但是通过机器学习、深度学习建模的朋友可能就会很苦恼，因为直接产出决策信号的模型可能是个黑盒子，很难明白为什么模型会产出某一个信号，甚至很多保守的私募基金把模型的可解释性放入了事前风控。其实，模型的可解释性是很容易做到的，难点在于研究员是否对模型有深入的思考和理解。
介绍
机器学习领域在过去十年中发生了显著的变化。从一个纯粹的学术和研究领域方向开始，我们已经看到了机器学习在各个领域都有着广泛的应用，如零售，技术，医疗保健，科学等等。在21世纪，数据科学和机器学习的重要目标已经转变为解决现实问题，自动完成复杂任务，让我们的生活变得更加轻松，而不仅仅是在实验室做实验发表论文。机器学习，统计学或深度学习模型工具已基本成型。像Capsule Networks这样的新模型在不断地被提出，但这些新模型被工业采用却需要几年时间。因此，在工业界中，数据科学或机器学习的主要焦点更多在于应用，而不是理论。这些模型可以在正确数据上有效应用来解决现实问题是至关重要的。
机器学习模型本质上就是一种算法，该算法试图从数据中学习潜在模式和关系，而不是通过代码构建一成不变的规则。所以，解释一个模型是如何在商业中起作用总会遇到一系列挑战。在某些领域，特别是在金融领域，比如保险、银行等，数据科学家们通常最终不得不使用更传统更简单的机器学习模型（线性模型或决策树）。原因是模型的可解释性对于企业解释模型的每一个决策至关重要。然而，这常常导致在性能上有所牺牲。复杂模型像如集成学习和神经网络通常表现出更好更精准的性能(因为真实的关系在本质上很少可以通过线性划分的)，然而，我们最终无法对模型决策做出合适的解释。为了解决和探讨这些差距，本文中，我会重点解释模型可解释性的重要及必要性。
动机
作为一名在企业工作的数据科学家并时常指导他人，我发现数据科学仍然常常被视为一个黑盒，它能用“魔法”或“炼金术”提供人们想要的东西。然而，严酷的现实是，如果不对模型进行合理足够的解释，现实世界的项目很少成功。如今，数据科学家通过构建模型并为业务提供解决方案。企业可能不知道模型实现的复杂细节，却要依靠这些模型做出决策，他们确实有权提出这样的问题：“我怎样才能相信你的模型？”或“你的模型是如何决策的”？”回答这些问题是数据科学实践者和研究人员数年来一直在尝试的事情。
数据科学家知道，模型解释性与模型性能之前有一个权衡。在这里，模型性能不是运行时间或执行性能，而是模型在做出预测时的准确度。有几种模型（包括简单的线性模型甚至基于树的模型），他们的预测的原理很好直观理解，但是需要牺牲模型性能，因为它们的产生的结果偏差或者方差很高（欠拟合：线性模型），或者容易过拟合（基于树的模型）。更复杂的模型，如集成模型和近期快速发展的深度学习通常会产生更好的预测性能，但被视为黑盒模型，因为要解释这些模型是如何真正做出决策是一件非常困难的事情。

虽然有些人说，知道模型性能好就行了，为什么还要知道它背后的原理呢？ 然而，作为人类，大多数决策基于逻辑和推理。 因此，人工智能（AI）作出决策的模式无疑会受到怀疑。 在很多现实情况下，有偏差的模型可能会产生真正的负面影响。 这包括预测潜在的犯罪、司法量刑、信用评分、欺诈发现、健康评估、贷款借款、自动驾驶等，其中模型的理解和解释是最重要的。 数据科学家、作家Cathy O’ Neil在她的著名著作《Weapons of Math Destruction》中也强调了这一点。
著名学者和作家凯特克劳福德在NIPS 2017主题演讲《The Trouble with Bias》中谈到了偏差在机器学习中的影响以及它对社会的影响。
有兴趣的读者也可以看看她在纽约时报的著名文章《 Artificial Intelligence’s White Guy Problem》，向我们展示了机器学习应用的案例，包括图像分类、犯罪风险预测、交付服务可用性等等，这些应用对黑人极不亲善。 如果我们想利用机器学习来解决这些问题，所有这些真实世界的场景都在告诉我们模型解释是多么的重要。
在过去的一年里，我在解决行业问题的同时也看到了对模型解释的需求，同时我也在写我的新书《Practical Machine Learning with Python2》。在这段时间里，我有机会与DataScience.com的优秀员工进行互动，他们非常清楚在机器学习模型中人类可解释性的必要性和重要性。他们也一直在积极研究解决方案，并开发了流行的python框架Skater。后续我们将深入研究Skater，并在本系列文章中做一些实际的模型解释。
理解模型解释
机器学习（尤其是深度学习）仅在最近几年才得到广泛的行业采用。因此，模型解释作为一个概念仍然主要是理论和主观的。
任何机器学习模型都有一个响应函数，试图映射和解释自（输入）变量和因（目标或响应）变量之间的关系和模式。
模型解释试图理解和解释响应函数做出的这些决定。模型解释的关键在于透明度以及人们理解模型决策的容易程度。模型解释的三个最重要的方面解释如下。
什么主导了模型预测？我们应该找出特征的相互作用，以了解在模型的决策策略中哪些特征可能是重要的。这确保了模型的公平性。
为什么模型做出某个特定决策？我们还应该能够验证为什么某些关键特征在预测期间推动某个模型所做出的某些决定。这确保了模型的可靠性。
我们如何相信模型预测？我们应该能够评估和验证任何数据点以及模型如何作出决策。对于模型按预期运行的直接利益相关者来说，这应该是可证明的，并且易于理解。这确保了模型的透明度。
可解释性是指人（包括机器学习中的非专家）能够理解模型在其决策过程中所做出的选择（怎么决策，为什么决策和决策了什么）。
在模型比较时，除了模型的性能，如果一个模型的决策比另一个模型的决策更容易被人类理解，则说该模型比另一个模型具有更好的可解释性。
模型解释的重要性
在解决机器学习问题时，数据科学家通常倾向于注意模型性能指标，如准确性、精确度和召回率等（毫无疑问，这很重要！）。但是，度量标准只能说明模型预测性决策的一部分内容。随着时间的推移，由于环境中各种因素造成的模型概念漂移，性能可能会发生变化。因此，了解什么促使模型作出某些决定是极为重要的。
我们中的一些人可能会认为模型已经工作得很好了，为什么还要深入挖掘呢？一定要记住，当解决现实世界中的数据科学问题时，为了让企业相信你的模型预测和决策，他们会不断提问“我为什么要信任你的模型？”，这非常合理。如果一个人患有癌症或糖尿病，如果一个人可能对社会构成风险，或者即使客户流失，您是否会满意于只是预测和做出决定（如何）的模型？也许另外一种会更好，如果我们可以更多地了解模型的决策过程（为什么以及如何），我们可能更喜欢它。这为我们提供了更多的透明度，说明为什么模型会做出某些决定，在某些情况下可能会出错，并且随着时间的推移它可以帮助我们在这些机器学习模型上建立一定的信任度。
这一部分关键的一点是，现在是时候停止将机器学习模型视为黑盒子，不仅尝试和分析数据，而且还要分析模型如何做出决策。实际上，走向这条道路的一些关键步骤是由著名论文《Why Should I Trust You？》（解释了任意分类器的预测）”开始的，由MT Ribeiro，S. Singh和C. Guestrin在SIGKDD 2016上介绍了LIME（Local Interpretable Model-Agnostic Explanations）（局部可解释模型 - 不可知论解释）的概念。
他们在论文中提到了一些值得记住的关键点。
然而，理解预测背后的原因在评估信任方面非常重要，如果计划基于预测采取行动，或者选择是否部署新模型，则对模型的信任是至关重要的。 无论人类是直接使用机器学习分类器作为工具还是在其他产品中部署模型，仍然存在一个至关重要的问题：如果用户不信任模型或预测，他们将不会使用它。
这是我们在本文中多次讨论的内容，也是决定数据科学项目在业界成功与否的关键因素之一。这就推动了模型解释的必要性和重要性。
模型解释方法的标准
对于模型解释方法的分类有特定的标准。在Christoph Molnar的“Interpretable Machine Learning，Making Guide for Making Black Box Models Explainable”中提到了一个很好的指导标准：
内在或事后？内在解释性是关于利用机器学习模型的，它本质上是解释性的(像线性模型、参数模型或基于树的模型)。事后解释性意味着选择和训练一个黑盒模型（集成方法或神经网络）并在训练后应用可解释性方法（特征重要性，部分依赖关系图）。我们将在我们的系列文章中更多地关注事后模型可解释的方法。
是针对某个模型的还是通用的？特定于模型的解释工具对固有模型解释方法非常具体，这些解释方法完全取决于每个模型的能力和特征。这可以是系数，p值，与回归模型相关的AIC分数，决策树的规则等等。通用的模型解释方法还是依赖于事后对模型的分析，可用于任何机器学习模型。通常通过分析特征输入和输出对来运行。根据定义，这些方法无法访问任何模型内部，如权重，约束或假设。
本地还是全局？这种解释的分类会谈到解释方法是解释单个预测还是整个模型行为？或者如果范围介于两者之间？我们将尽快讨论更多关于局部和全局的解释。
这并不是对可解释方法进行分类的一套完整的标准，因为这仍然是一个新兴的领域，但这可以是一个很好的标准，可以在多种方法之间进行比较和对比。
模型解释的范围
我们如何界定解释的范围和界限？一些有用的方面可以是模型的透明度，公平性和可靠性。本地还是全局模型解释是定义模型解释范围的明确方法。
全局解释性
这就是要试图理解“模型如何做出预测？”和“模型的子集如何影响模型决策？”。为了一次理解和解释整个模型，我们需要全局解释。全局可解释性是指能够基于完整数据集上的依赖（响应）变量和独立（预测）特征之间的条件相互作用来解释和理解模型决策。试图理解特征的相互作用和重要性，往往是理解全局解释的好的一步。当然，在尝试分析交互时，在超过两个或三个维度后对特征进行可视化变得非常困难。因此，经常查看可能会影响全局知识模型预测的模块化部分和特征子集，对全局解释是有所帮助的。完整的模型结构知识，假设和约束是全局解释所必需的。
局部解释性
这就是要了解“为什么模型会为单个实例做出特定决策？”以及“为什么模型会为一组实例做出特定决策？”。对于局部的可解释性，我们不关心模型的内在结构或假设，我们把它当作一个黑箱子。为了理解单个数据点的预测决策，我们专门关注该数据点，并在该点附近的特征空间中查看局部子区域，并尝试根据此局部区域了解该点的模型决策。局部数据分布和特征空间可能表现完全不同，并提供更准确的解释而不是全局解释。局部可解释模型 - 不可知论解释（LIME）框架是一种很好的方法，可用于模型不可知的局部解释。我们可以结合使用全局解释和局部解释来解释一组实例的模型决策。
模型透明度
这就是要了解“从算法和特征中创建模型的过程如何？”。我们知道，典型的机器学习模型都是关于利用一个算法在数据特征之上构建一个表示，将输入映射到潜在的输出(响应)。模型的透明性可以尝试理解模型如何构建的更多技术细节，以及影响其决策的因素。这可以是神经网络的权值，CNN滤波器的权值，线性模型系数，节点和决策树的分割。然而，由于企业对这些技术细节可能并不十分熟悉，试图用不可知的局部和全局解释方法来解释模型决策有助于展示模型的透明度。
结论
模型可解释是一个对现实世界机器学习项目非常重要的一件事情。让我们试着去研究人类可解释的机器学习，让每个人都打开机器学习模型的黑箱，并帮助人们增加对模型决策的信任。
写在最后：模型解释性很重要，这能够加深我们对模型的信心，尤其是在金融市场中，当模型持续回撤时，信心比黄金还重要。之前有一个私募团队使用了StockRanker策略，但是迟迟不肯上实盘，后来在弄清楚模型的理论原理和每一步细节、处理流程后，终于有信心上实盘，实盘前期遇到回撤也能明白是正常情况，并非模型预测失效，扛住前期的回撤后策略净值开始上升。因此，机器学习模型可解释很重要，模型也是可以解释的，只是需要研究员付出更多的心血

基于实例的解释

第7章 基于实例的解释

基于实例的解释方法选择数据集的特定实例来解释机器学习模型的行为或解释底层数据分布。

基于实例的解释大多与模型无关，因为它们使任何机器学习模型都更具可解释性。与模型无关方法的区别在于，基于实例的方法通过选择数据集的实例而不是通过创建特征摘要（例如特征重要性或部分依赖性）来解释模型）。

只有当我们能够以人类可理解的方式表示数据实例时，基于实例的解释才有意义。这适用于图像，因为我们可以直接查看它们。一般来说，如果实例的特征值携带更多上下文，则基于实例的方法效果很好，这意味着数据具有结构，就像图像或文本一样。以有意义的方式表示表格数据更具挑战性，因为一个实例可能包含数百或数千个（结构较少的）特征。列出所有特征值来描述一个实例通常是没有用的。如果只有少数几个特征或者我们有办法总结一个实例，它会很好地工作。

基于实例的解释帮助人类构建机器学习模型的心智模型以及机器学习模型已经训练过的数据。它尤其有助于理解复杂的数据分布。但我所说的基于实例的解释是什么意思？我们经常在工作和日常生活中使用它们。让我们从一些例子¹开始。

一位医生看到一名患者出现异常咳嗽和轻微发烧。病人的症状让她想起了她多年前有过类似症状的另一个病人。她怀疑她目前的患者可能患有同样的疾病，因此她采集了血液样本来检测这种特定疾病。

一位数据科学家为他的一个客户开展了一个新项目：分析导致键盘生产机器故障的风险因素。数据科学家记得他从事的一个类似项目，并重用了旧项目中的部分代码，因为他认为客户想要相同的分析。

一只小猫坐在燃烧的无人居住的房子的窗台上。消防部门已经到了，其中一名消防员思考了片刻，他是否可以冒险进入大楼去救小猫。他回忆起自己作为消防员生活中的类似案例：缓慢燃烧一段时间的旧木屋往往不稳定，最终倒塌。因为这个案子的相似性，他决定不进去，因为房子倒塌的风险太大了。幸运的是，小猫从窗户跳了出来，安全着陆，没有人在火灾中受到伤害。美满结局。

这些故事说明了我们人类如何通过例子或类比思考。基于实例的解释的蓝图是：事物 B 与事物 A 相似，而 A 导致 Y，所以我预测 B 也会导致 Y。

隐含地，一些机器学习方法是基于实例的。[决策树]](#tree)根据对预测目标很重要的特征中数据点的相似性，将数据划分为节点。

决策树通过查找相似的实例（=在同一终端节点中）并返回这些实例的结果的平均值作为预测来获取新数据实例的预测。

k-最近邻 (knn) 方法明确适用于基于实例的预测。

对于一个新实例，knn 模型定位 k 个最近的邻居（例如，k=3 个最近的实例）并返回这些邻居的结果的平均值作为预测。knn 的预测可以通过返回 k 个邻居来解释，同样，只有当我们有一种好的方法来表示单个实例时，它才有意义。

以下解释方法均基于实例：

• 反事实解释告诉我们实例必须如何改变才能显着改变其预测。通过创建反事实实例，我们了解模型如何进行预测并可以解释单个预测。
• 对抗性示例是用来欺骗机器学习模型的反事实。重点是翻转预测而不是解释它。
• 原型是从数据中选择的具有代表性的实例，而驳议是那些原型没有很好地代表的实例。²
• 有影响的实例是对预测模型的参数或预测本身最有影响的训练数据点。识别和分析有影响的实例有助于发现数据问题、调试模型并更好地了解模型的行为。
• k-最近邻模型：基于实例的（可解释的）机器学习模型。

7.1 反事实解释

作者：Susanne Dandl 和 Christoph Molnar

devtools::load_all()
set.seed(42)

反事实解释以如下形式描述了一种因果情况：“如果 $X$ 没有发生，$Y$ 就不会发生”。
例如：“如果我没有喝一口这种热咖啡，我就不会烫到我的舌头”。
事件 $Y$ 是我烧了我的舌头；
因为 $X$ 是我喝了热咖啡。
反事实思考需要想象一个与观察到的事实相矛盾的假设现实（例如，一个我没有喝过热咖啡的世界），因此得名“反事实”。
与其他动物相比，反事实思考的能力使我们人类如此聪明。

在可解释的机器学习中，反事实解释可用于解释单个实例的预测。
“事件”是一个实例的预测结果，“原因”是该实例的特定特征值，它们输入到模型中并“导致”某个预测。
显示为图表，输入和预测之间的关系非常简单：
特征值导致预测。

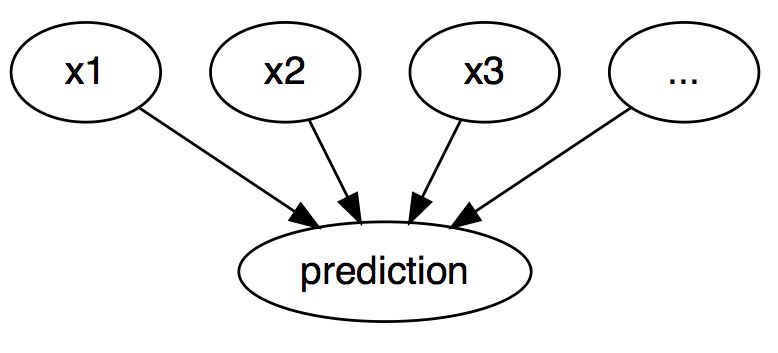
即使实际上输入与要预测的结果之间的关系可能不是因果关系，我们也可以将模型的输入视为预测的原因。

鉴于这个简单的图表，很容易看出我们如何模拟反事实来预测机器学习模型：
我们只是在进行预测之前更改实例的特征值，然后分析预测如何变化。
我们对预测以相关方式发生变化的场景感兴趣，例如预测类别的翻转（例如，信用申请被接受或拒绝），或者预测达到某个阈值（例如，癌症的概率达到10%）。
预测的反事实解释描述了将预测更改为预定义输出的特征值的最小变化。

有模型无关和模型特定的反事实解释方法，但在本章中，我们关注仅适用于模型输入和输出（而不是特定模型的内部结构）的模型无关方法。
这些方法在[模型无关章节]（#agnostic）中也很熟悉，因为解释可以表示为特征值差异的总结（“改变特征A和B以改变预测”）。
但是反事实解释本身就是一个新的实例，所以它存在于本章中（“从实例X开始，改变A和B得到一个反事实实例”）。
与 原型 不同，反事实不一定是来自训练数据的实际实例，而是可以是特征值的新组合。

在讨论如何创建反事实之前，我想讨论一些反事实的用例以及一个好的反事实解释是什么样的。

在第一个示例中，彼得申请贷款并被（机器学习驱动的）银行软件拒绝。
他想知道为什么他的申请被拒绝，以及如何提高获得贷款的机会。
“为什么”的问题可以表述为反事实：
将预测从拒绝变为批准的特征（收入、信用卡数量、年龄……）的最小变化是什么？
一种可能的答案可能是：
如果彼得每年多赚 10,000 美元，他就会得到贷款。
或者，如果彼得拥有较少的信用卡并且五年前没有拖欠贷款，他就会得到贷款。
彼得永远不会知道拒绝的原因，因为银行对透明度不感兴趣，但那是另一回事了。

在我们的第二个示例中，我们想要解释一个模型，该模型通过反事实解释来预测连续结果。
Anna 想出租她的公寓，但她不确定要收取多少费用，因此她决定训练一个机器学习模型来预测租金。
当然，由于 Anna 是一名数据科学家，这就是她解决问题的方式。
在输入有关大小、位置、是否允许携带宠物等所有详细信息后，模特告诉她可以收取 900 欧元的费用。
她预计 1000 欧元或更多，但她信任她的模型并决定使用公寓的特征值，看看如何提高公寓的价值。
她发现如果该公寓再大 $15m^2$，则可以以超过 1000 欧元的价格出租。
有趣但不可操作的知识，因为她无法扩大她的公寓。
最后，通过仅调整她控制下的特征值（内置厨房是/否、允许携带宠物是/否、地板类型等），她发现如果她允许携带宠物并安装隔热效果更好的窗户，她可以收取 1000 欧元。
Anna 直觉地使用反事实来改变结果。

反事实是 人性化的解释，因为它们与当前实例形成对比，并且因为它们是选择性的，这意味着它们通常专注于少数特征变化。
但反事实受到“罗生门效应”的影响。
罗生门是一部日本电影，其中一个武士被谋杀是由不同的人讲述的。
每个故事都同样很好地解释了结果，但故事相互矛盾。
反事实也可能发生同样的情况，因为通常有多种不同的反事实解释。
每个反事实都讲述了如何达到某个结果的不同“故事”。
一个反事实可能会说改变特征 A，另一个反事实可能会说保持 A 不变但改变特征 B，这是矛盾的。
可以通过报告所有反事实解释或通过制定标准来评估反事实并选择最佳解释来解决多重事实的问题。

说到标准，我们如何定义一个好的反事实解释？
首先，反事实解释的用户定义了实例预测中的相关变化（=替代现实）。
一个明显的第一个要求是一个反事实实例尽可能接近地产生预定义的预测。
并不总是可以找到与预定义预测相反的事实。
例如，在具有两个类（稀有类和频繁类）的分类设置中，模型可能总是将实例分类为频繁类。
更改特征值以使预测标签从频繁类翻转到稀有类可能是不可能的。
因此，我们希望放宽反事实的预测必须与预定义结果完全匹配的要求。
在分类示例中，我们可以寻找一个反事实，其中稀有类的预测概率增加到 $10\%$，而不是当前的 $2\%$。
那么问题是，使预测概率从 $2\%$ 变为 $10\%$（或接近 $10\%$）的特征的最小变化是多少？

另一个质量标准是一个反事实应该与关于特征值的实例尽可能相似。
例如，如果我们同时具有离散特征和连续特征，则可以使用曼哈顿距离或高尔距离来测量两个实例之间的距离。
反事实不仅应该接近原始实例，还应该尽可能少地改变特征。
为了衡量这个指标中反事实解释的好坏，我们可以简单地计算变化特征的数量，或者用花哨的数学术语，测量反事实和实际实例之间的 $L_0$ 范数。

第三，通常需要生成多种不同的反事实解释，以便决策主体可以使用多种可行的方式来产生不同的结果。
例如，继续我们的贷款示例，一种反事实解释可能建议仅将收入翻倍以获得贷款，而另一种反事实解释可能建议转移到附近的城市并增加少量收入以获得贷款。
可以注意到，虽然第一个反事实可能对某些人来说是可能的，但后者可能对其他人来说更可行。
因此，除了为决策主体提供不同的方式来获得期望的结果之外，多样性还使“多样化”的个体能够改变对他们来说方便的特征。

最后一个要求是一个反事实实例应该具有可能的特征值。
对于公寓面积为负数或房间数量设置为 200 的租金示例，生成反事实解释是没有意义的。
如果根据数据的联合分布，反事实很可能就更好了，例如，10 个房间和 $20m^2$ 的公寓不应该被视为反事实解释。
理想情况下，如果增加平方米数量，也应该提出增加房间数量。

7.1.1 生成反事实解释

产生反事实解释的一种简单而幼稚的方法是通过反复试验进行搜索。
这种方法涉及随机更改感兴趣实例的特征值，并在预测到所需输出时停止。
就像安娜试图找到她可以收取更多租金的公寓版本的例子一样。
但是有比试错更好的方法。
首先，我们根据上述标准定义损失函数。
这种损失将感兴趣的实例、反事实和期望的（反事实）结果作为输入。
然后，我们可以找到使用优化算法最小化这种损失的反事实解释。
许多方法都以这种方式进行，但在损失函数和优化方法的定义上有所不同。

在下文中，我们关注其中两个：首先，Wachter 等人的一个。(2017)³，他引入了反事实解释作为解释方法，其次是 Dandl 等人的方法。(2020)⁴ 考虑到上述所有四个标准。

7.1.1.1 Wachter 等人的方法

Wachter 等人建议尽量减少以下损失：

$$L(x,x^{\prime },y^{\prime },\lambda )=\lambda \cdot (\hat{f}(x^{\prime })-y^{\prime }{)}^2+d(x,x^{\prime })$$

第一项是模型预测反事实 $x^{\prime }$ 和期望结果 $y^{\prime }$ 之间的二次距离，用户必须提前定义。
第二项是要解释的实例 $x$ 与反事实 $x^{\prime }$ 之间的距离 d。
损失衡量反事实的预测结果与预定义结果的距离以及反事实与感兴趣的实例的距离。
距离函数 d 定义为使用每个特征的逆中值绝对偏差 (MAD) 加权的曼哈顿距离。

$$d(x,x^{\prime })=\sum _{j=1}^p\frac{|x_j-x_j^{\prime }|}{MA{D}_j}$$

总距离是所有 $p$ 个特征距离的总和，即实例 $x$ 和反事实 $x^{\prime }$ 之间的特征值的绝对差值。
特征距离通过特征 $j$ 在数据集上的绝对偏差中值的倒数来缩放，定义为：

$$MA{D}_j={\text{median}}_{i\in 1,\dots ,n}(|x_{i,j}-{\text{median}}_{l\in 1,\dots ,n}(x_{l,j})|)$$

向量的中值是向量值的一半较大而另一半较小的值。
MAD 等价于特征的方差，但不是使用均值作为中心并在平方距离上求和，而是使用中值作为中心并在绝对距离上求和。
所提出的距离函数具有优于欧几里得距离的优点：

它对异常值更稳健。
使用 MAD 进行缩放对于使所有功能达到相同的比例是必要的——无论你以平方米还是平方英尺来衡量公寓的大小都无关紧要。

参数 $\lambda$ 平衡预测中的距离（第一项）与特征值中的距离（第二项）。
对于给定的 $\lambda$，损失被求解并返回一个反事实的 $x^{\prime }$ 。
$\lambda$的较高值意味着我们更喜欢预测接近预期结果 $y^{\prime }$ 的反事实，较低的值意味着我们更喜欢与特征值中的 $x$ 非常相似的反事实 $x^{\prime }$ 。
如果 $\lambda$ 非常大，则预测最接近 $y^{\prime }$ 的实例将被选中，无论它离 $x$ 多远。
最终，用户必须决定如何平衡反事实的预测与期望结果相匹配的要求与反事实与 $x$ 相似的要求。
该方法的作者建议不要选择 $\lambda$ 的值，而是选择允许反事实实例的预测与 $y^{\prime }$ 相差多远的容差 $ϵ$。
这个约束可以写成：

$$|\hat{f}(x^{\prime })-y^{\prime }|\le ϵ$$

为了最小化这个损失函数，可以使用任何合适的优化算法，例如 Nelder-Mead。
如果你可以访问机器学习模型的梯度，则可以使用 ADAM 等基于梯度的方法。
要解释的实例 $x$ 、所需的输出 $y^{\prime }$ 和容差参数 $ϵ$ 必须提前设置。
x’ 的损失函数最小化，并且（局部）最优反事实 $x^{\prime }$ 返回，同时增加 $\lambda$ 直到找到足够接近的解（= 在容差参数内）：

$$\arg \underset{x^{\prime }}{\min }\underset{\lambda }{\max }L(x,x^{\prime },y^{\prime },\lambda ).$$

总的来说，产生反事实的方法很简单：

1. 选择要解释的实例 x x x以上是关于机器学习模型可解释的重要及必要性的主要内容，如果未能解决你的问题，请参考以下文章

   机器学习模型可解释性的6种Python工具包，总有一款适合你！

   终于有人把可解释机器学习讲明白了

   终于有人把可解释机器学习讲明白了

   干货|全面介绍微软开源可解释机器学习框架InterpretML

   基于实例的解释

   基于实例的解释