梯度下降法是啥？

Posted 2023-05-12

梯度下降法，是一种基于搜索的最优化方法，它其实不是一个机器学习算法，但是在机器学习领域，许多算法都是以梯度下降法为基础的，它的主要作用是寻找目标函数的最优解。

在求解损失函数的最小值时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值。反过来，如果我们需要求解损失函数的最大值，这时就需要用梯度上升法来迭代了。在机器学习中，基于基本的梯度下降法发展了两种梯度下降方法，分别为随机梯度下降法和批量梯度下降法。

常用的梯度下降法有3种不同的形式：

（1）批量梯度下降法，简称 BGD，使用所有样本，比较耗时；

（2）随机梯度下降法，简称 SGD，随机选择一个样本，简单高效；

（3）小批量梯度下降法，简称 MBGD，使用少量的样本，这是一个折中的办法。

参考技术A

梯度下降法简单来说就是一种寻找目标函数最小化的方法。

梯度下降法，是一种基于搜索的最优化方法，它其实不是一个机器学习算法，但是在机器学习领域，许多算法都是以梯度下降法为基础的，它的主要作用是寻找目标函数的最优解。

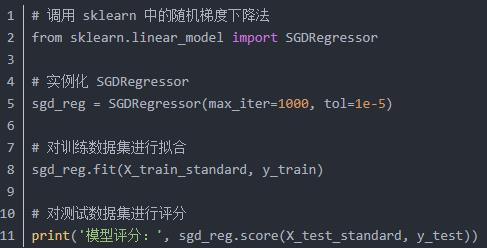
因为随机梯度下降法是一个随机的算法，所以返回的模型评分结果也是一个随机数，每次运行的结果可能都会不一样。

常用的梯度下降法有 3 种不同的形式：

（1）批量梯度下降法，简称 BGD，使用所有样本，比较耗时。

（2）随机梯度下降法，简称 SGD，随机选择一个样本，简单高效。

（3）小批量梯度下降法，简称 MBGD，使用少量的样本，这是一个折中的办法。

梯度下降的替代方案是啥？

【中文标题】梯度下降的替代方案是啥？

【英文标题】：What are alternatives of Gradient Descent?梯度下降的替代方案是什么？

【发布时间】：2014-06-26 14:28:18

【问题描述】：

梯度下降存在局部最小值问题。我们需要运行梯度下降指数时间来找到全局最小值。

谁能告诉我梯度下降的任何替代方案及其优缺点。

谢谢。

【问题讨论】：

特别是在神经网络的情况下。

【参考方案1】：

请参阅my masters thesis 以获得非常相似的列表：

神经网络的优化算法

基于梯度 梯度下降的风格（仅一阶梯度）： 随机梯度下降： 小批量梯度下降： 学习率调度： 动量： RProp 和小批量版本 RMSProp AdaGrad Adadelta (paper) 指数衰减学习率 性能调度 Newbob 调度 Quickprop Nesterov 加速梯度 (NAG)：Explanation 高阶梯度 Newton's method: Typically not possible 准牛顿法 BFGS L-BFGS 不确定它是如何工作的 Adam（自适应矩估计） AdaMax 共轭梯度 替代品 遗传算法 模拟退火 Twiddle 马尔可夫随机场（graphcut/mincut）

单纯形算法

用于运筹学环境中的线性优化，但显然也用于神经网络 (source)

您可能还想看看我关于 optimization basics 的文章和在 Alec Radfords 上的精美 GIF：1 和 2，例如

其他有趣的资源是：

An overview of gradient descent optimization algorithms

权衡

我认为所有已发布的优化算法都有一些具有优势的场景。一般的权衡是：

您一步就能取得多少进步？ 一步计算的速度有多快？ 算法可以处理多少数据？ 是否保证找到局部最小值？ 优化算法对您的函数有什么要求？ （例如，一次、两次或三次可微）

【参考方案2】：

与使用的方法相比，与最小化函数有关的问题更多，如果找到真正的全局最小值很重要，则使用模拟退火等方法。这将能够找到全局最小值，但可能需要很长时间。

对于神经网络，局部最小值不一定是个大问题。一些局部最小值是由于您可以通过置换隐藏层单元或否定网络的输入和输出权重等来获得功能相同的模型。此外，如果局部最小值只是略微非最优，那么性能上的差异将很小，因此并不重要。最后，这是很重要的一点，拟合神经网络的关键问题是过拟合，因此积极寻找成本函数的全局最小值可能会导致过拟合和模型性能不佳。

添加正则化项，例如权重衰减，可以帮助平滑成本函数，这可以稍微减少局部最小值的问题，无论如何我都会推荐它作为避免过度拟合的一种方法。

然而，在神经网络中避免局部最小值的最佳方法是使用高斯过程模型（或径向基函数神经网络），它与局部最小值的问题较少。

【讨论】：

关于高斯过程的最后一点，你能引用一些参考资料吗？

【参考方案3】：

局部最小值是解空间的属性，而不是优化方法。这是一般神经网络的问题。凸方法（例如 SVM）之所以受欢迎，主要是因为它。

【参考方案4】：

已经证明，在高维空间中，卡在局部最小值中的可能性很小，因为在每个维度中，所有导数都为零是不太可能的。 （来源 Andrew NG Coursera DeepLearning Specialization）这也解释了为什么梯度下降如此有效。

【参考方案5】：

Extreme Learning Machines 本质上，它们是一个神经网络，其中将输入连接到隐藏节点的权重是随机分配的，并且永远不会更新。隐藏节点和输出之间的权重是通过使用矩阵求逆求解线性方程一步来学习的。