排序算法

Posted 2020-11-22 littlebanana

最近大二的dalao给大一宝宝讲了排序算法，发现自己也好久没有看排序了( sort真香 )。

所以来总结一波排序。
大一宝宝们看完选择性的吸收哦~

总结：

排序算法	平均复杂度	空间复杂度	稳定性
冒泡排序	O(n2)	O(1)	稳定
选择排序	O(n2)	O(1)	不稳定
插入排序	O(n2)	O(1)	稳定
希尔排序	O(n log n)	O(1)	不稳定
归并排序	O(n log n)	O(n)	稳定
快速排序	O(n log n)	O(log n)	不稳定
桶排序	O(n+k)	O(n+k)	稳定

( 自己的实力只允许这几种排序 /肥宅大哭 )

冒泡排序( BubbleSort )

• 算法步骤
  • 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
  • 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
  • 针对所有的元素重复以上的步骤，除了最后一个。
  • 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

• 动画演示

  

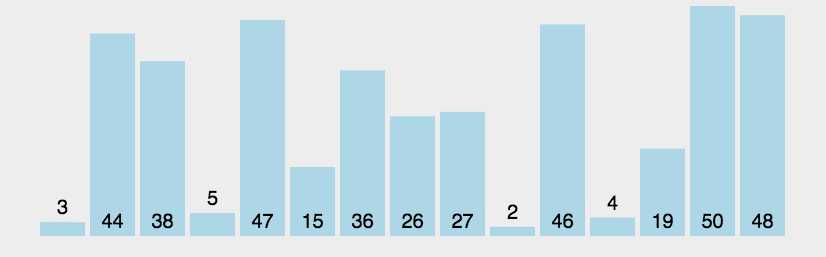
• 参考代码

  #include<cstdio>
  void BuddleSort(int a[],int n) {
      for(int i=0 ; i<n-1 ; i++){
          for(int j=0 ; j<n-i-1 ; j++){
              if(a[j]>a[j+1]){
                  int swap=a[j];
                  a[j]=a[j+1];
                  a[j+1]=swap;
              }
          }
      }
  } 
  int main(void) {
      int a[]={6, 9，8，4，5，2，1，3，7};
      int n=sizeof(a)/sizeof(int);
      BuddleSort(a,n);
      printf("冒泡排序结果：");
  
      for (int i = 0 ; i < n ; i++){
          printf("%d ", a[i]);
      }
      return 0;
  }

选择排序( SelectSort )

• 算法步骤
  • 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置 。
  • 再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
  • 复第二步，直到所有元素均排序完毕。

• 动画演示

  

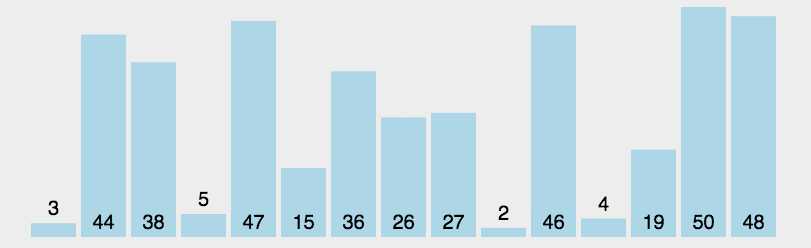
• 参考代码：

  #include<cstdio>
  void SelectSort(int a[],int n) {
      for(int i=0;i<n-1;i++){
          int min=i;  //存放数组最小值的位置 
          for(int j=i+1;j<n;j++){
              if(a[j]<a[min]){
                  min=j;   //找出最小值，并记录位置 
              }
           } 
           if(min!=i) //最小元素与第i个元素互换位置 {
              int swap=a[min];
               a[min]=a[i];
               a[i]=swap;
           }
      }
  }
  int main(void) {
      int a[]={8,9,7,1,5,4,2,3,6};
      int n=sizeof(a)/sizeof(int);
      SelectSort(a,n);
       printf("选择排序结果：");
      for (int i = 0; i < n; i++){
          printf("%d ", a[i]);
      }
      printf("
  ");
      return 0;
  }

插入排序( InsertSort )

• 算法步骤：

  • 将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。
  • 从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）

• 动画演示：

  

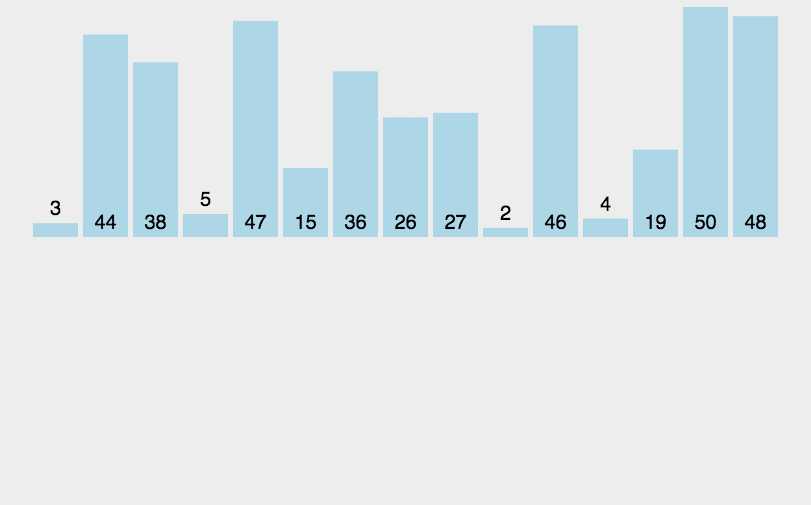
• 参考代码

  #include<cstdio>
  void InsertSort(int a[],int n) {
      for(int i=0 ; i<n ; i++){
          int j=i-1;
          if(a[i]<a[i-1]){ //若第i个元素小于第i-1个元素,移动有序序列插入------大于的话则直接插入 
              int swap=a[i];  //存储将要排序的元素 
              a[i]=a[i-1];   //向后移动一个元素 
  
              while(swap < a[j]) {//查询将要插入的位置
                  a[j+1]=a[j];
                  j--;       //元素后移 
              }
            a[j+1]=swap;//循环结束 插入到指定位置 
        }    
      }
  }
  int main(void) {
      int a[] = { 9,7,8,2,5,1,3,6,4};
      int n = sizeof(a)/sizeof(int);
      InsertSort(a, n);
      printf("排序好的数组为：");
      for (int i=0 ; i<n ; i++) {
          printf("%d", a[i]);
      }
      printf("
  ");
      return 0;
  }

希尔排序( ShellSort )

• 算法步骤：
  • 选择一个增量序列 t1，t2，……，tk，其中 ti > tj, tk = 1。
  • 按增量序列个数 k，对序列进行 k 趟排序。
  • 每趟排序，根据对应的增量 ti，将待排序列分割成若干长度为 m 的子序列，分别对各子表进行直接插入排序。仅增量因子为 1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。
  • 个人认为，核心是让数据在小规模内有序，减小递增量使得整体有序。

• 动画演示：

  

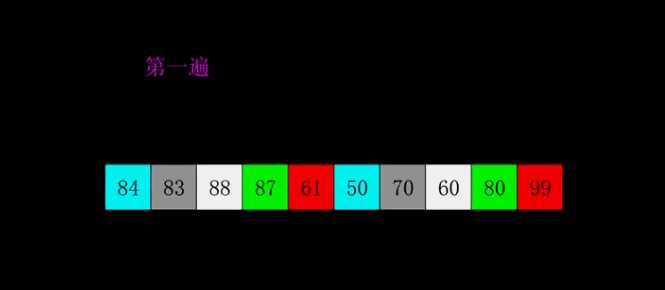
• 参考代码：

  #include<iostream>
  using namespace std;
  
  void print(int a[], int n){  
      for(int j= 0; j<n; j++){  
          cout<<a[j] <<"  ";  
      }  
      cout<<endl;  
  }
  
  void shellSort(int a[], int n) {
      int i,j,gap;   // gap为步长，每次减为原来的一半。
      for (gap = n / 2; gap > 0; gap /= 2){
          // 共gap个组，对每一组都执行直接插入排序
          for (i = 0 ;i < gap; i++){
              for (j = i + gap; j < n; j += gap) { 
                  // 如果a[j] < a[j-gap]，则寻找a[j]位置，并将后面数据的位置都后移。
                  if (a[j] < a[j - gap]){
                      int tmp = a[j];
                      int k = j - gap;
                      while (k >= 0 && a[k] > tmp){
                          a[k + gap] = a[k];
                          k -= gap;
                      }
                      a[k + gap] = tmp;
                  }
              }
          }
      }
  }
  
  int main(void) {  
      int a[10] = {8,1,9,7,2,4,5,6,10,3};   
      shellSort(a,10);  
      cout<<"排序结果：";  
      print(a,10);  
    return 0; 
  } 

归并排序( Merge Sort )

• 算法步骤：
  • 把长度为n的输入序列分成两个长度为n/2的子序列。
  • 对这两个子序列分别采用归并排序。
  • 将两个排序好的子序列合并成一个最终的排序序列。

• 动画演示：

  

• 参考代码：

  #include<iostream>
  
  using namespace std;
  
  void mergearray(int a[],int first,int mid,int last,int t[]) {
    int i=first,j=mid+1;
    int n=mid,m=last;
    int k=0;
    while(i<=n && j<=m){
        if(a[i]<=a[j]){
            t[k++]=a[i++];
        }   
        else{
            t[k++]=a[j++];
        }
    }   
    while(i<=n)
        t[k++]=a[i++];  
    while(j<=m)
        t[k++]=a[j++];  
    for(i=0;i<k;i++)
        a[first+i]=t[i];
  }
  
  void mergesort(int a[],int first,int last,int t[]) {
    if(first < last){
        int mid=(first+last)/2;
        mergesort(a,first,mid,t);
        mergesort(a,mid+1,last,t);
        mergearray(a,first,mid,last,t);
    }
  }
  
  
  int MergeSort(int a[],int len) {
    int *temp=new int [len];
  
    if(temp==NULL)  return 0;
    else    mergesort(a,0,len-1,temp);
    delete []temp;
  
    return 1;
  } 
  
  int main(void) {
    int n;
    cin>>n;
    int *arr = new int[n];
  
    for(int i=0 ; i<n ; i++){
        cin>>arr[i];
    }
  
    MergeSort(arr,n);
  
    for(int i=0 ; i<n ; i++){
        cout<<arr[i]<<" ";
    }
    return 0;
  }

快速排序( QuickSort )

• 算法步骤：
  • 从数列中挑出一个元素，称为 “基准”（pivot）。
  • 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作 。
  • 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序 。

• 动画演示：

  

• 参考代码：

  #include <stdio.h> 
  #include <string.h> 
  int a[100 + 1]; 
  void quickSort(int l, int r, int a[]) { 
    int i = l, j = r; int mid = (i + r) / 2; 
    do {
        while (a[i] < a[mid]) ++i;//循环结束时，a[i] >= a[mid] 
        while (a[mid] < a[j]) --j;//循环结束时，a[j] <= a[mid] 
            if (i <= j) { 
                int temp = a[i]; 
                a[i] = a[j]; 
                a[j] = temp; ++i; --j;//交换数值后继续搜索 
            } 
    } while (i <= j);//我们需要结束时i > j 
    if (l < j) quickSort(l, j, a);
    //若未找到两个数的边界，则递归搜索左右区间。l < j则j - l > 0 
    //即l与j之间还有数字可以继续 
    if (i < r) quickSort(i, r, a);
  }
  int main(void) { 
    int n; 
    memset(a, 0, sizeof(a)); 
    printf("请输入你要排序多少个数："); 
    scanf("%d", &n); printf("
  请输入这%d个数字
  ", n); 
    for (int i = 1; i <= n; ++i) { 
        scanf("%d", a + i); 
    } 
    quickSort(1, n, a); 
    for (int i = 1; i <= n; ++i) { 
        printf("%d ", a[i]); 
    }
    printf("
  "); 
    return 0; 
  }

桶排序( BucketSort )

• 算法步骤：
  • 设置一个定量的数组当作空桶 。
  • 遍历输入数据，并且把数据一个一个放到对应的桶里去 。
  • 对每个不是空的桶进行排序 。
  • 从不是空的桶里把排好序的数据拼接起来 。

• 动画展示