已知一棵二叉树的中序和前序序列如下，求该二叉树的后序序列,并画出二叉树

Posted 2023-05-12

中序序列：c，b，d，e，a，g，I，h，j，f
前序序列：a，b，c，d，e，f，g，h，I，j

#include <iostream>。

#include <cstring>。

#define MAX 50+3。

using namespace std;

typedef char Elem_Type;

typedef struct BiTree。

Elem_Type data;//数据。

truct BiTree *Lchild;//左孩子。

struct BiTree *Rchild;//右孩子。

BiTree;      //要查找的元素  查找的地方    数组的长度。

int Search_Num(Elem_Type num,Elem_Type *array,int len)。

for(int i=0; i<len; i++)。

if(array[i] == num)。

return i;

//return -1;//没有找到。

                           //中序遍历    后序遍历     中序长度

BiTree *Resume_BiTree(Elem_Type *center,Elem_Type *back,int len)

if(len <= 0)

return NULL;

BiTree *temp = new BiTree;

temp->data = *back;

int index = Search_Num(*back,center,len);

temp->Rchild = Resume_BiTree(center+index+1,back-1,len-index-1);

temp->Lchild = Resume_BiTree(center,back-len+index,index);

return temp;

void PreOrderTraverse(BiTree *root)//前序遍历

if( root != NULL)

cout<<root->data;

PreOrderTraverse(root->Lchild);

PreOrderTraverse(root->Rchild);

    

int main(void)

Elem_Type *inorder  = new Elem_Type [MAX];//中序

Elem_Type *postorde = new Elem_Type [MAX];//后序

int t;cin>>t;

while(t--)

cin>>inorder;cin>>postorde;

BiTree *root =

Resume_BiTree(inorder,postorde+strlen(postorde)-1,strlen(inorder));

PreOrderTraverse(root);

cout<<endl;

return 0;

扩展资料：

(1)空二叉树——如图(a)；

(2)只有一个根结点的二叉树——如图(b)；

(3)只有左子树——如图(c)；

(4)只有右子树——如图(d)；

(5)完全二叉树——如图(e)。

注意：尽管二叉树与树有许多相似之处，但二叉树不是树的特殊情形。 [1] 

(1)完全二叉树——若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树。

(2)满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。

(3)平衡二叉树——平衡二叉树又被称为AVL树（区别于AVL算法），它是一棵二叉排序树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

二叉树是树一种特殊情形，是一种更简单而且应用更加广泛的树。

参考资料来源：百度百科-二叉树

参考技术A

我给楼主讲讲思想吧。

前序排序可以让你知道树的根节点是a，左孩子是b

将中序这样看 cbde    a    glhjf

这样就分出了a的左右子树各所有的节点。

从cbde 前序必然先读根，所以读b，可以这样看 c  b  de

这样又分出来。如此反复，可以画出树。然后根据中序检查，某些只有一孩子的，到底是左孩子还是右孩子，因为左右孩子必然导致中序不一样。

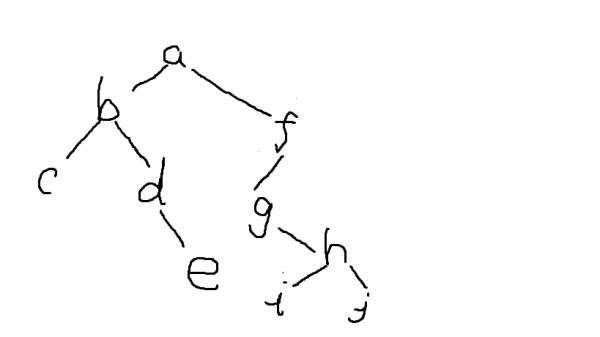
后序：c e d b i j h g f a

本回答被提问者和网友采纳 参考技术B

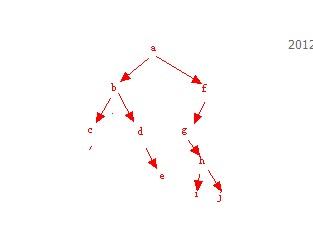
后序序列：c,e,d,b,i,j,h,g,f,a

二叉树如图：

洛谷 P1229遍历问题

 P1229 遍历问题

题目描述

我们都很熟悉二叉树的前序、中序、后序遍历，在数据结构中常提出这样的问题：已知一棵二叉树的前序和中序遍历，求它的后序遍历，相应的，已知一棵二叉树的后序遍历和中序遍历序列你也能求出它的前序遍历。然而给定一棵二叉树的前序和后序遍历，你却不能确定其中序遍历序列，考虑如下图中的几棵二叉树：

所有这些二叉树都有着相同的前序遍历和后序遍历，但中序遍历却不相同。

输入输出格式

输入格式：

 

输A数据共两行，第一行表示该二叉树的前序遍历结果s1，第二行表示该二叉树的后序遍历结果s2。

 

输出格式：

 

输出可能的中序遍历序列的总数，结果不超过长整型数。

 

输入输出样例

输入样例#1：

abc                           
cba

输出样例#1：

4



喜闻乐见的Code

#include<cstdio>
#include<cstring>
using namespace std;
#define maxn 30
char a[maxn],b[maxn];
int main() {
	scanf("%s%s",a,b);
	int cnt=0;
	for(int i=1;i<strlen(a);i++)
		for(int j=0;j<strlen(b);j++)
			if(a[i]==b[j]&&a[i-1]==b[j+1]) cnt++;
	printf("%d",1<<cnt);
	return 0;
}