当n=5,m=4时，面值为(1,3,11,15,32)的5种邮票，如何求出其最大连续邮资区间1到70？？

Posted 2023-05-11

求高手相助啊！！急急.......这种连续邮资问题的最大连续邮资区间是怎样求出来的？如果贴4张都是面值为32的不是更大吗？先谢了！！！！

1. 问题描述
假设某国家发行了n种不同面值的邮票，并且规定每张信封上最多只允许贴m张邮票。连续部资问题要求对于给定的n和m的值，给出邮票面值的最佳设计，在1张信封上贴出从邮资1开始，增量为1的最大连续邮资区间。例如，当n=5和m=4时，面值为1、3、1.
15、32的5种邮票可以贴出邮资的最大连续邮资区间是1～70。
2.算法设计
对于连续邮资问题，用n元组×1:n]表示n种不同的邮票面值，并约定它们从小到大排列。x[1=1是唯一的选择。此时的最大连续邮资区间是[1:m]。接下来，x[2]的可取值范围是[2:m+1]。在一般情况下，已选定x[1:7-1]，最大连续邮资区间是[1:r]，接下来x的可取值范围是[x[i-1]+1:r+1]。由此可以看出，在用回溯法解连续邮资问题时，可以用树表示其解空间。该解空间树中各结点的度随x的不同取值而变化。
在下面的解连续邮资问题的回溯法中，类Stamp的数据成员记录解空间中结点信息。maxvalue记录当前已找到的最大连续邮资区间。bestx是相应的当前最优解。数组y记录当前已选定的邮票面值×[1：能贴出各种邮资所需的最少邮票张数。换句话说，y[k]是用不超过m张面值为×[1：的邮票贴出邮资k所需的最少邮票数。
在算法Backtrack中，当n时，算法搜索至叶结点，得到新的邮票面值设计方案x[1：n。如果该方案能贴出的最大连续邮资区间大于当前已找到的最大连续邮资区间maxvalue，则更新当前最优值maxvalue和相应的最优解bestx。
当i n时，当前扩展结点Z是解空间中的内部结点。在该结点处，x[1：i-1]能贴出的最大连续邮资区间为r-1。因此，在结点Z处，x的可取值范围是[x[i-1]+1:r]，从而，结点Z有一x[i-1]个儿子结点。算法对当前扩展结点Z的每个儿子结点，以深度优先的方式递归地对相应子树进行搜索。 参考技术A 问题叙述不全

2021-08-17：谷歌面试题扩展版，面值为1~N的牌组成一组，每次你从组里等概率的抽出1~N中的一张，下次抽会换一个新的组，有无限组，当累加和＜a时，你将一直抽牌，当累加和＞=a且＜b时，你将获胜

2021-08-17：谷歌面试题扩展版，面值为1_{N的牌组成一组，每次你从组里等概率的抽出1}N中的一张，下次抽会换一个新的组，有无限组，当累加和<a时，你将一直抽牌，当累加和>=a且<b时，你将获胜，当累加和>=b时，你将失败。返回获胜的概率，给定的参数为N，a，b。

福大大 答案2021-08-17：

递归。一张牌一张牌累加，概率累加即可。
时间复杂度：O(N*b)。

代码用golang编写。代码如下：

package main

import "fmt"

func main() {
    ret := f2(5, 2, 3)
    fmt.Println(ret)
}
func f1() float64 {
    return p1(0)
}

// 游戏的规则，如上
// 当你来到cur这个累加和的时候，获胜概率是多少返回！
func p1(cur int) float64 {
    if cur >= 17 && cur < 21 {
        return 1.0
    }
    if cur >= 21 {
        return 0.0
    }
    w := 0.0
    for i := 1; i <= 10; i++ {
        w += p1(cur + i)
    }
    return w / 10
}

// 谷歌面试题扩展版
// 面值为1~N的牌组成一组，
// 每次你从组里等概率的抽出1~N中的一张
// 下次抽会换一个新的组，有无限组
// 当累加和<a时，你将一直抽牌
// 当累加和>=a且<b时，你将获胜
// 当累加和>=b时，你将失败
// 返回获胜的概率，给定的参数为N，a，b
func f2(N int, a int, b int) float64 {
    if N < 1 || a >= b || a < 0 || b < 0 {
        return 0.0
    }
    if b-a >= N {
        return 1.0
    }
    // 所有参数都合法，并且b-a < N
    return p2(0, N, a, b)
}

// 游戏规则，如上，int N, int a, int b，固定参数！
// cur，目前到达了cur的累加和
// 返回赢的概率
func p2(cur int, N int, a int, b int) float64 {
    if cur >= a && cur < b {
        return 1.0
    }
    if cur >= b {
        return 0.0
    }
    w := 0.0
    for i := 1; i <= N; i++ {
        w += p2(cur+i, N, a, b)
    }
    return float64(w) / float64(N)
}

// f2的改进版本，用到了观察位置优化枚举的技巧
// 可以课上讲一下
func f3(N int, a int, b int) float64 {
    if N < 1 || a >= b || a < 0 || b < 0 {
        return 0.0
    }
    if b-a >= N {
        return 1.0
    }
    return p3(0, N, a, b)
}

func p3(cur int, N int, a int, b int) float64 {
    if cur >= a && cur < b {
        return 1.0
    }
    if cur >= b {
        return 0.0
    }
    if cur == a-1 {
        return 1.0 * float64(b-a) / float64(N)
    }
    w := p3(cur+1, N, a, b) + p3(cur+1, N, a, b)*float64(N)
    if cur+1+N < b {
        w -= p3(cur+1+N, N, a, b)
    }
    return float64(w) / float64(N)
}

// f3的改进版本的动态规划
// 可以课上讲一下
func f4(N int, a int, b int) float64 {
    if N < 1 || a >= b || a < 0 || b < 0 {
        return 0.0
    }
    if b-a >= N {
        return 1.0
    }
    dp := make([]float64, b)
    for i := a; i < b; i++ {
        dp[i] = 1.0
    }
    if a-1 >= 0 {
        dp[a-1] = 1.0 * float64(b-a) / float64(N)
    }
    for cur := a - 2; cur >= 0; cur-- {
        w := dp[cur+1] + dp[cur+1]*float64(N)
        if cur+1+N < b {
            w -= dp[cur+1+N]
        }
        dp[cur] = float64(w) / float64(N)
    }
    return dp[0]
}

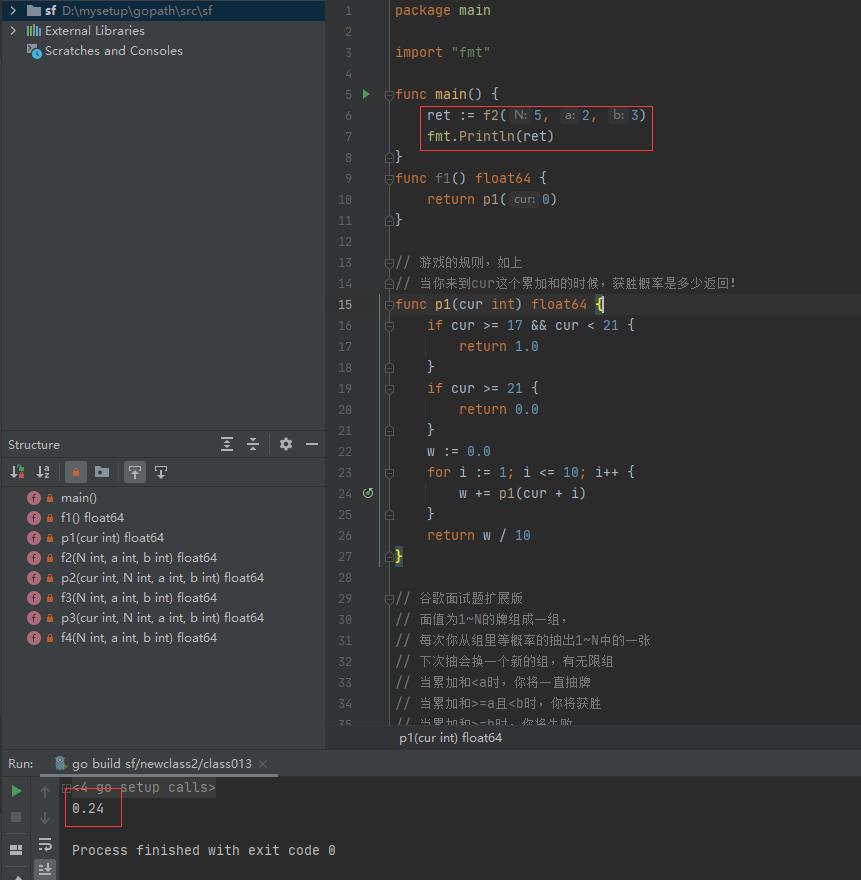
执行结果如下：

---

左神java代码