消除左递归

Posted 2020-11-22 rinkong0403

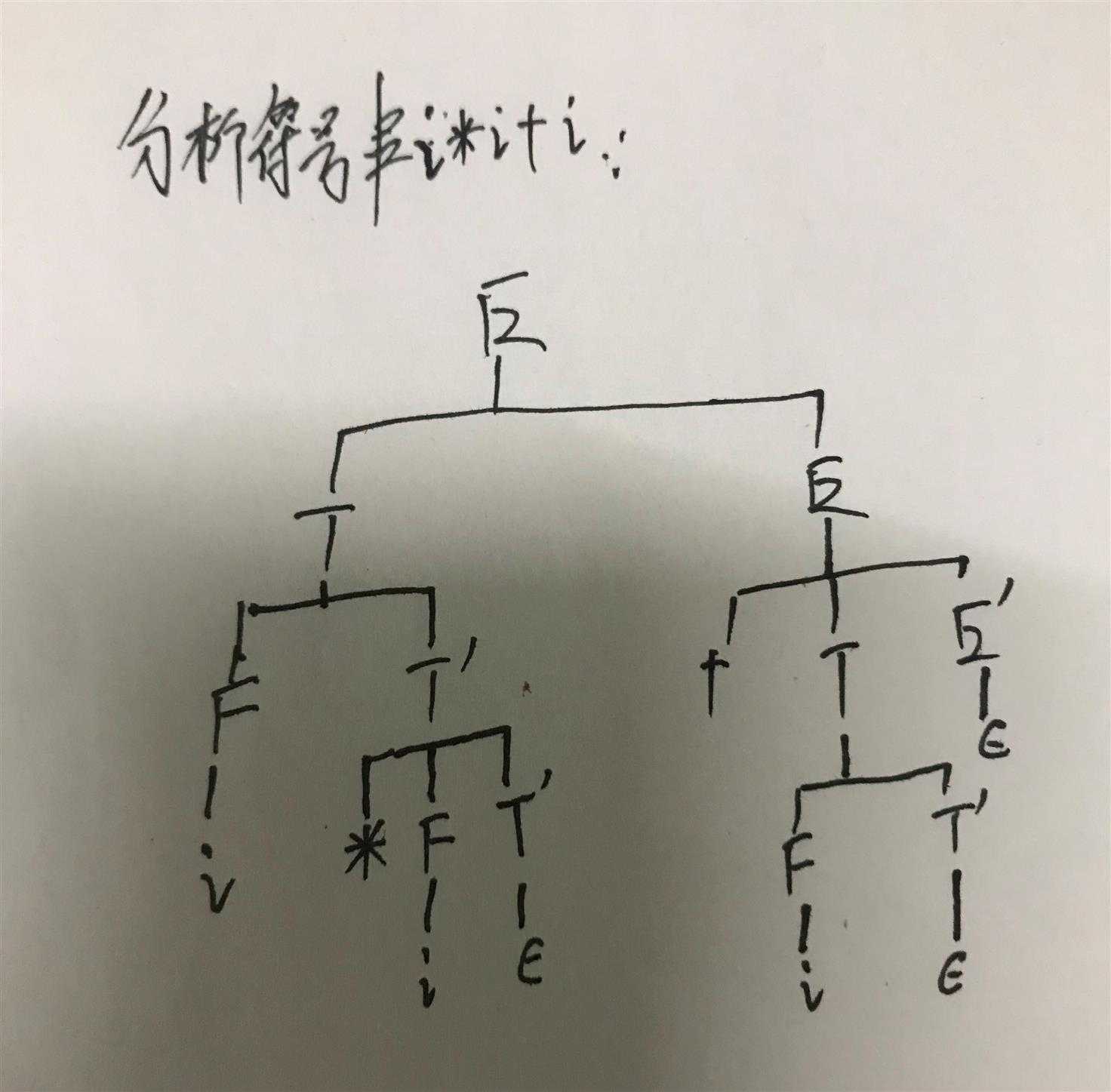
1.将以下文法消除左递归，分析符号串 i*i+i 。

   并分别求FIRST集、FOLLOW集，和SELECT集

     E -> E+T | T

     T -> T*F | F

     F -> (E) | i

消除左递归：

　E→TE‘

　　E‘→+TE‘|ε

　　T→FT‘

　　T‘→*FT‘|ε

　　F→(E)|i

FIRST集

FIRST(TE‘)={T}

　　FIRST(+TE‘)={+}

　　FIRST(ε)={ε}

　　FIRST(FT‘)={F}

　　FIRST(*FT‘)={*}

　　FIRST((E))={(}

　　FIRST(i)={i}

　FOLLOW集

　　FOLLOW(E)={)}

　　FOLLOW(E‘)={#}

　　FOLLOW(T)={E‘}

　　FOLLOW(T‘)={#}

　　FOLLOW(F)={#}

Select(E -> TE‘) = First(TE‘) = {T}

Select(E‘ -> +TE‘) = First(+TE‘) = {+}

Select(E‘ -> ε) = (First(ε)-{ε})∪Follow(E‘) = {)}

Select(T -> FT‘) = First(FT‘) = {F}

Select(T‘ -> *F) = First(*F) = {*}

Select(T‘ -> ε) = (First(ε)-{ε})∪Follow(T‘) = {ε}

Select(F -> (E)) = First((E)) = {(}

Select(F -> i ) = First(i) = {i}

 2.P101练习7（2）（3）文法改写，并分别求FIRST集、FOLLOW集，和SELECT集

(2)

A -> aABe|a

B -> Bb|d

提取左公因子：

　　A→aA‘

　　A‘→ABe|ε

消除公因式：

　　B→dB‘

　　B‘→bB‘|ε

 1.First集：

First(aA‘) = {a}

First(ABe) = {a}

First(ε) = {ε}

First(dB‘) = {d}

First(bB‘) = {b}

2.Follow集：

Follow(A) = {Be}

Follow(A‘) = {ε}

Follow(B) = {e}

Follow(B‘) = {ε}

3.Select集：

Select(A -> aA‘) = First(aA‘) = {a}

Select(A‘ -> ABe) = First(ABe) = {a}

Select(A‘ -> ε) =  (First(ε)-{ε})∪Follow(A‘)) = {ε}

Select(B -> dB‘）= First(dB‘) = {d}

Select(B‘ -> bB‘) = First(bB‘) = {b}

Select(B‘ -> ε) = (First(ε)-{ε})∪Follow(B‘)) = {ε}

  (3)

S -> Aa|b

A ->SB

B ->ab

②代入①：

　　S -> SBa|b

消除左递归：

　　S - > bS‘

　　S‘ -> BaS‘|ε

　　B -> ab

 1.First集：

First(SBa) = {a}

First(b) = {b}

First(bS‘) = {b}

First(BaS‘) = {a}

First(ε) = {ε}

First(ab) = {a}

2.Follow集：

Follow(S) = {B}

Follow(S‘) = {ε}

Follow(B) = {S‘}

3.Select集：

Select(S -> SBa) = First(SBa) = {a}

Select(S -> b) = First(b) = {b}

Select(S -> bS‘) = First(bS‘) = {b}

Select(S‘ -> BaS‘) = First(BaS‘) = {a}

Select(S‘ -> ε) =  (First(ε)-{ε})∪Follow(S‘)) = {ε}

Select(B -> ab) = First(ab) = {a}

 3.求以下文法的FIRST集、FOLLOW集和SELECT集。

S->Ap
A->a |ε
A->cA

A->aA

1.First集：

First(S) = {a,c,p}

First(a) = {a}

First(ε) = {ε}

First(cA) = {c}

FIrst(aA) = {a}

 

2.Follow集：

Follow(S) = {ε}

Follow(A) ={p}

 

3.Select集：

Select(S->Ap) = First(Ap) ={p}

Select(A -> a) = FIrst(a) = {a}

Select(A -> ε) = First(ε) = {ε}

Select(A -> cA) = First(cA) ={c}

Select(A -> aA) =First(aA) = {a}

 S->Ap

S->Bq
A->a
A->cA
B->b
B->dB

 1.First集：

First(Ap) = {a,c}

First(Bq) = {b,d}

First(a) = {a}

First(cA) = {c}

First(b) = {b}

First(dB) = {d}

2.Follow集：

Follow(S) = {ε}

Follow(A) = {p}

Follow(B) = {q}

3.Select集：

Select(S -> Ap) = First(Ap) = {a,c

Select(S - >Bq) = First(Bq) = {q}

Select(A - > a) = First(a) = {a}

Select(A -> cA) = First(cA) = {c}

Select(B -> b）= FIrst(b) = {b}

Select(B ->dB) = FIrst(dB) = {d}