R语言分布的卡方拟合优度检验
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了R语言分布的卡方拟合优度检验相关的知识,希望对你有一定的参考价值。
参考技术A卡方拟合优度检验,用于衡量观测频数与期望频数之间的差异
一般地,假设总体分r类 ,分布假设检验问题
在原假设下, 期望频数 :
假设从总体中随机抽取n个样本,并记 为样本中分到类中的个数,称为 观测频数 。
K.Pearson在原假设 成立下:
因此,在显著性水平 下,拒绝域为
p-value = 0.9254>0.05,则不应拒绝原假设,孟德尔的结论是成立的。
同理,可以先计算出
某美发店上半年各月顾客数量如下,请问该店各月顾客数是否为均匀分布?
我们用R语言来模拟一下实际操作
R语言实验结果与示例完全相同。
R语言 | 卡方检验(Chi-squaretest)
卡方检验在计数资料中的应用,包括推断两个总体率或构成比之间有无差别、多个总体率或构成比之间有无差别、多个样本率间的多重比较、两个分类变量之间有无关联性、多维列联表的分析和频数分布拟合优度的卡方检验。
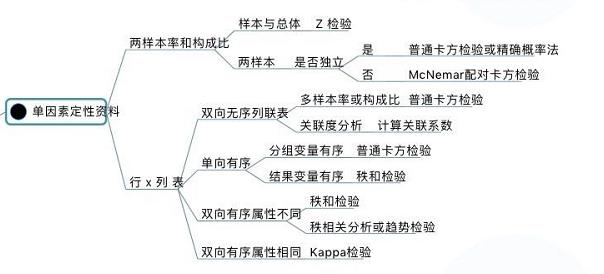
下面分别介绍计数资料怎么进行卡方检验。
目 录
1. 四格表资料的卡方检验
1.1 数据集数据
1.2 向量或矩阵数据
1.3 chisq.test()函数
2. Fisher确切概率法
3. 配对四格表资料的卡方检验
3.1 b+c < 40
3.2 b+c ≥ 40
3.3 mcnemar.test()函数
4. Cochran-Mantel-Haenszel检验
4.1 mantelhaen.test()函数
4.2 数据集形式的数据
4.3 向量或数组数据
4.4 计算各层OR值
4.5 Breslow-Day检验
4.6 BreslowDayTest()函数
4.7 WoolfTest()函数
5. 计算列联系数
6. 频数分布拟合优度的卡方检验
1. 四格表资料的卡方检验
1.1 数据集数据
选用survival包的colon数据集。
library(survival) #加载内置数据集的包
data(colon) # 加载数据集
mytable <- xtabs(~ status + sex, data= colon); mytable
chisq.test(mytable) # 进行连续性校正
chisq.test(mytable, correct = FALSE) # 不进行连续性校正
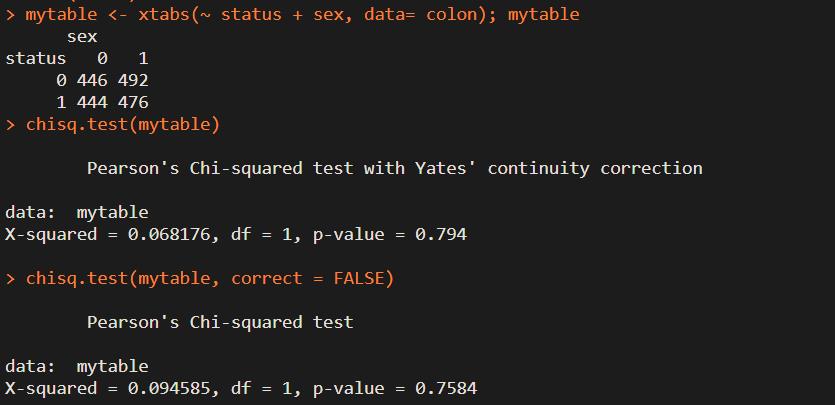
无论是否进行连续性校正,结果都显示p值>0.05,接受原假设,说明sex和status无关。
还可以输出卡方检验摘要:
chisq.test(mytable)$observed # 实际频数(和mytable一样)
chisq.test(mytable)$expected # 期望频数
chisq.test(mytable)$residuals # Pearson 残差
chisq.test(mytable)$stdres # 标准化残差
1.2 向量或矩阵数据
compare<-matrix(c(706,792,184,176), nr = 2,
dimnames = list(c("male", "female"),
c("Yes", "No")));compare
chisq.test(compare)
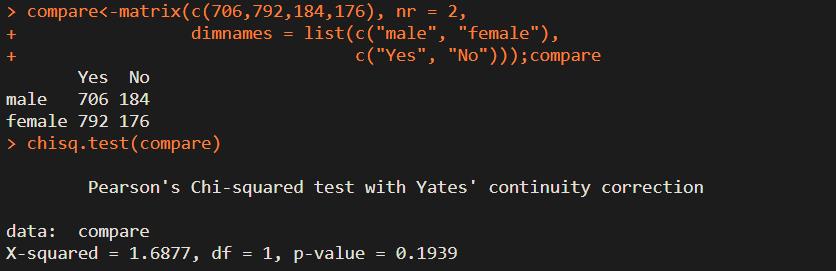
注意:在使用chisq.test()函数计算时,要注意单元格的期望频数。如果所有单元格频数都不为零,并且所有单元的期望频数≥5,那么Pearson卡方检验是合理的,否则会显示警告信息。
如果在计算时出现警告信息,表明表中单元格期望频数有<5的值,这可能会使卡方近似无效。

如果数据不满足卡方检验的条件时,应使用Fisher精确检验。
1.3 chisq.test()函数
chisq.test()函数可以进行卡方列联表检验和拟合优度检验。
chisq.test(x, y = NULL, # x是由数据构成的向量或矩阵,y是数据向量(当x为矩阵时,y忽略)
correct = TRUE, # 逻辑词,默认为TRUE,在计算2x2列联表的检验统计量时是否使用连续性校正
p = rep(1/length(x), length(x)), # p是原假设落在小区间的理论概率,默认值表示均匀分布.
# P是和x长度相同的概率向量,P值如果输入有负值,会返回错误信息。
rescale.p = FALSE, # 逻辑词,为TRUE,则p将缩放成和为1的向量;为FALSE,如果p向量和≠1,则会返回错误信息
simulate.p.value = FALSE, # 为TRUE则不进行连续性校正,根据蒙特卡洛检验计算p值
B = 2000) # B为整数,在蒙特卡洛检验中使用的重复次数。
对于2x2的列联表,参数correct的默认值为TRUE,即使用Yate连续修正,目的是提高P值,避免"有显著差异"不可靠的情况发生;
2. Fisher确切概率法
在样本较小时(单元的期望频数<5),需要用Fisher精确检验来完成独立性检验。Fisher检验开始是针对2x2四格表提出的,当卡方检验的条件不满足时,可以使用精确检验。
fisher.test(x, y = NULL, # 参数x为二维列联表形式的矩阵,或者由因子构成的对象。y为因子构成的向量,当x为矩阵时,此值无效。
workspace = 200000, # 正整数,表示用于网络算法工作空间的大小
hybrid = FALSE, # 逻辑词,仅用于2x2列联表,为FALSE时(默认值)表示精确计算概率,取TRUE表示用混合算法计算概率。
hybridPars = c(expect = 5, percent = 80, Emin = 1),
control = list(), or = 1, # 为列表,指定低水平算法的组成,or为优势比的原假设,默认值为1,仅用于2x2列联表。
alternative = "two.sided", # 备择假设,默认值"two.sided",表示双侧检验(不独立),“less”表示单侧小于检验(负相关);“greater”表示单侧大于检验(正相关)。
conf.int = TRUE, # 逻辑词,为TRUE则给出优势比的置信区间。
conf.level = 0.95, # 置信水平,默认0.95
simulate.p.value = FALSE, B = 2000) # 逻辑词,为TRUE,表示用Monto Carlo方法计算P值,B为正整数,表示Monto Carlo重复的次数。
例:研究COPD与吸烟之间的关系,调查了52名COPD患者和33名非COPD患者吸烟的人数。
compare<-matrix(c(49,28,3,5),nr = 2, byrow = TRUE,
dimnames = list(c("smoke", "Notsmoke"),
c("COPD", "normal")))
compare
chisq.test(compare)$expected # 查看期望频数
fisher.test(compare) # 进行fisher精确检验
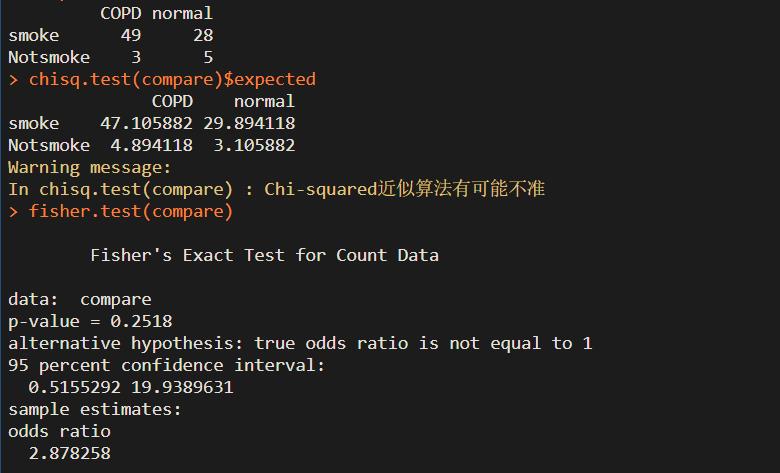
因为p-value=0.2518>0.05,并且优势比的置信区间包含1,故接受原假设, 认为吸烟与COPD无关。
3. 配对四格表资料的卡方检验
计数资料的配对设计常用于两种检验方法、培养方法、诊断方法的比较。特点是对样本中各观察单位分别用两种方法处理,然后观察两种处理方法的某两分类变量的计数结果。
假设检验为McNemar卡方检验,检验统计量有两种(分b+c ≥ 40和b+c < 40的情况)。该法一般用于样本含量不太大的资料。
-
当 b+c < 40时,使用连续性校正,即correct=TRUE。 -
当 b+c ≥ 40时,不使用连续性校正,即correct=FALSE。
3.1 b+c < 40
例:某实验室分别用乳胶凝集法和免疫荧光法对58名可疑系统性红斑狼疮患者血清中抗核抗体进行测定,问这两种方法的检测结果有无差别?
X <- matrix(c(11,2,12,33),
nrow = 2,
byrow = FALSE,
dimnames = list(免疫荧光法 = c("+","-"),乳胶凝集法 = c("+","-")));X
# 乳胶凝集法
# 免疫荧光法 + -
# + 11 12
# - 2 33
mcnemar.test(X,correct=TRUE)
# McNemar's Chi-squared test with continuity correction
# data: X
# McNemar's chi-squared = 5.7857, df = 1, p-value = 0.01616
结论:p-value = 0.01616 < 0.05,可以认为两种方法的检测结果不同,免疫荧光法的阳性检测率较高
3.2 b+c ≥ 40
例:某医院同时用A、B两种方法测定160份痰标本中的抗酸杆菌,问A、B两种方法的检出率有无显著性差异?
X <- matrix(c(52,20,35,53),
nrow = 2,
byrow = FALSE,
dimnames = list(A方法 = c("+","-"),B方法 = c("+","-")));X
# B方法
# A方法 + -
# + 52 35
# - 20 53
mcnemar.test(X,correct=FALSE)
# McNemar's Chi-squared test
# data: X
# McNemar's chi-squared = 4.0909, df = 1, p-value = 0.04311
结论:p-value = 0.04311 < 0.05,可以认为两种方法的检测结果不同。
3.3 mcnemar.test()函数
使用mcnemar.test()函数进行McNemar检验。
mcnemar.test(x, y=NULL, #参数x为二维列联表形式的矩阵,或者由因子构成的对象。y为因子构成的向量,当x为矩阵时,此值无效。
correct=TRUE) #逻辑词,默认为TRUE,仅在2x2列联表下进行连续校正。
4. Cochran-Mantel-Haenszel检验
CMH检验可以理解为分层卡方检验,CMH检验用于高维列联表的分析,即在控制了某一个或几个混杂因素(分层变量)之后,检验二维RxC表中行变量与列变量之间是否存在统计学关联。
假设检验:
H0:为任一层的行变量X与列变量Y均不相关;
H1:为至少有一层X与Y存在统计学关联。
当H0成立时,CMH统计量渐近卡方分布。需要注意的是,当各层间行变量与列变量相关的方向不一致时,CMH统计量的检验效能较低。
根据行变量X和列变量Y的类型不同,CMH卡方统计量包括:
1.相关统计量:适用于双向有序分类变量;
2.方差分析统计量:也称行平均得分统计量,适用于列变量Y为有序分类变量;
3.一般关联统计量:适用双向无序分类变量,目的是检验X和Y是否存在关联性。
4.1 mantelhaen.test()函数
mantelhaen.test()函数用来进行CMH卡方检验。其原假设是,两个分类变量在第三个变量的每一层中都是条件独立的。
mantelhaen.test(x, y = NULL, # x为数组形式的三维列联表,行与列的维度至少为2,最后一个维度为分层变量;
# 或者x为至少有2个水平的因子,y也为至少有2个水平的因子,如果x为三维数组时,y忽略;
z = NULL, # 至少有2个水平的因子,表示哪一层对应x中的元素,哪一层对应y的元素,如果x为三维数组,则z忽略;
alternative = c("two.sided", "less", "greater"), # 备择假设,默认为"two.sided"双侧检验;
correct = TRUE, # 逻辑词,计算检验统计量时使用连续性校正;
exact = FALSE, # 逻辑词,是否计算精确检验;
conf.level = 0.95) # 置信水平,默认0.95
注意:数组或向量不允许存在缺失值,x,y,z必须为长度相同的数字向量。
4.2 数据集形式的数据
选用survival包的colon数据集。xtabs()函数可以基于三个或多个分类变量生成多维列联表。
mytable <- xtabs(~ rx + status + sex, data= colon); mytable
mantelhaen.test(mytable)
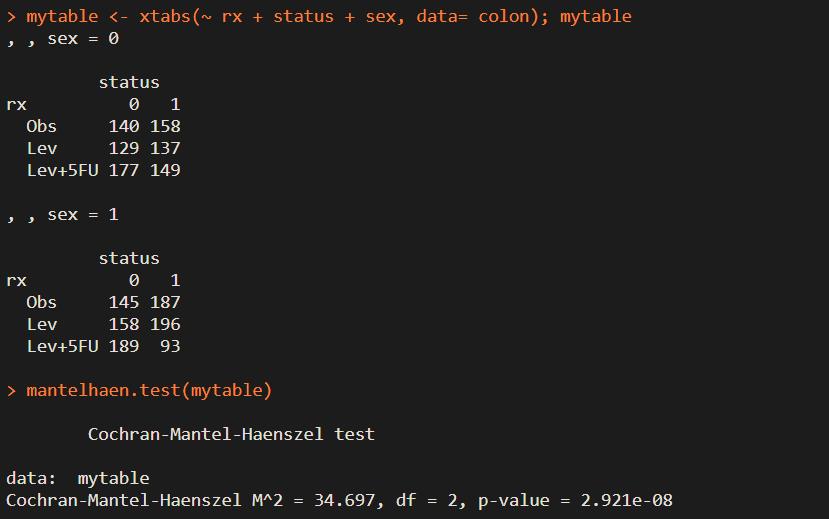
结果中p-value = 2.921e-08,表明患者接受的治疗与结局状态在性别的每一水平下并不独立。
4.3 向量或数组数据
为研究心肌梗死与近期使用避孕药之间的关系,采用病例对照研究方法调查了234 名心肌梗死病人与1742名对照使用口服避孕药的状况。考虑到年龄是混杂因素,按照年龄分层后结果见下表。试分析排除了年龄因素的影响后,心肌梗死是否与近期使用口服避孕药有关。
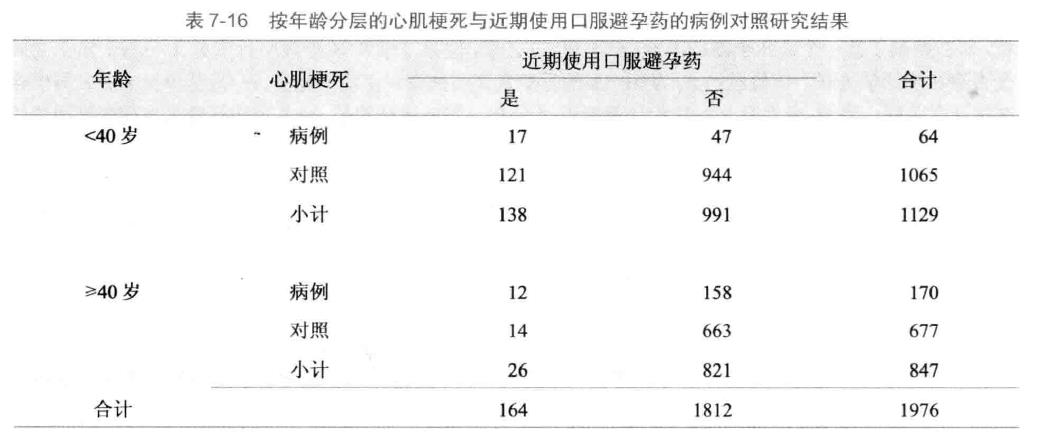
mydata <- array(c(17, 121, 47, 944,
12, 14, 158, 663),
dim = c(2, 2, 2),
dimnames = list(心肌梗死 = c("病例", "对照"),
近期使用口服避孕药 = c("是", "否"),
年龄 = c("< 40岁", "≥ 40岁")))
mydata
mantelhaen.test(mydata, correct = F) # 经典的2x2xk水平 CMH 检验
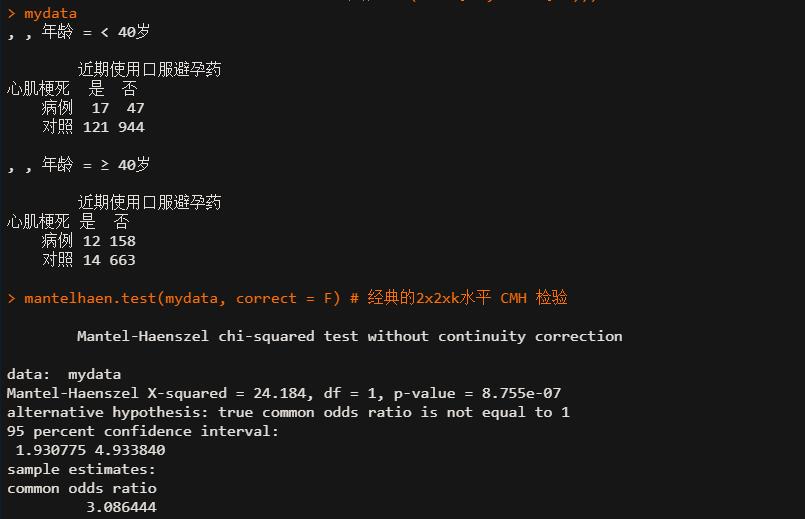
结果显示P<0.001,按a=0.05的检验水准拒绝H0,接受H1,可认为控制了年龄的影响后,心肌梗死与近期服用口服避孕药有关。
4.4 计算各层OR值
apply(mydata, 3, function(x) (x[1,1]*x[2,2])/(x[1,2]*x[2,1]))
# < 40岁 ≥ 40岁
# 2.821874 3.596745
4.5 Breslow-Day检验
对于分层病例对照研究或队列研究资料,通常应用Breslow-Day检验对各层的效应值(OR或RR)进行齐性检验。
若不拒绝齐性假设(p>0.05),才可依据CMH检验的结果推断出暴露因素是否与疾病相关。如果相关,可进一步用Mantel-Haenszel法估计OR或RR值及其可信区间。
若拒绝了齐性假设(p<0.05),则提示分层变量与暴露因素间存在交互作用,此时CMH检验的结果不能说明问题,可进行多元logistic回归分析。
4.6 BreslowDayTest()函数
BreslowDayTest(x, # 2x2xk列联表
OR = NA, # 要检验的OR值,默认使用Mantel-Haenszel估算值。
correct = FALSE) # 为TRUE,则使用Tarone调整的Breslow-Day检验
library(DescTools) # 加载包
BreslowDayTest(mydata) # 进行Breslow-Day检验
# Breslow-Day test on Homogeneity of Odds Ratios
# data: mydata
# X-squared = 0.23409, df = 1, p-value = 0.6285
BreslowDayTest(mydata, correct = TRUE) # Tarone校正的Breslow-Day检验
# Breslow-Day Test on Homogeneity of Odds Ratios (with Tarone correction)
# data: mydata
# X-squared = 0.23369, df = 1, p-value = 0.6288
结果为P=0.6285,可认为两年龄组口服避孕药对心肌梗死的总体OR值同质:用Mantel-Haenszel法估计OR值及其95%可信区间为3.09(1.93-4.93)。
4.7 WoolfTest()函数
除了BreslowDayTest()函数外,WoolfTest()函数也可以对2x2xk列联表的同质性进行检验。
WoolfTest(x) # x为2x2xk列联表,最后一个维度为分层变量
WoolfTest(mydata)
# Woolf Test on Homogeneity of Odds Ratios (no 3-Way assoc.)
# data: mydata
# X-squared = 0.23358, df = 1, p-value = 0.6289
结论和BreslowDayTest检验一样。
5. 计算列联系数
若行x列表资料的两个分类变量都为无序分类变量,进行多个样本率的比较、样本构成比的比较都可以用卡方检验,也就是使用chisq.test()函数来计算。
若得知两个分类变量之间有关联性,需进一步分析关系的密切程度时,可计算Pearson列联系数。
列联系数C (Contingency Coeff) 取值为0-1之间,0表示完全独立, 1表示完全相关;愈接近于1,关系愈密切。
vcd包中的assocstats()函数可以用来计算二维列联表的phi系数、列联系数和Cramer’s V系数。
例:测得某地 5801 人的 ABO 血型和 MN 血型结果如下,问这两种血型之间是否有关联。

mytable <- matrix(c(431, 388, 495, 137,
490, 410, 587, 179,
902, 800, 950, 32),
nrow = 4, byrow = FALSE,
dimnames = list(ABO血型 = c("O","A","B","AB"),
MN血型 = c("M","N","MN")))
mytable
chisq.test(mytable) # 判断两分类变量有无关联性
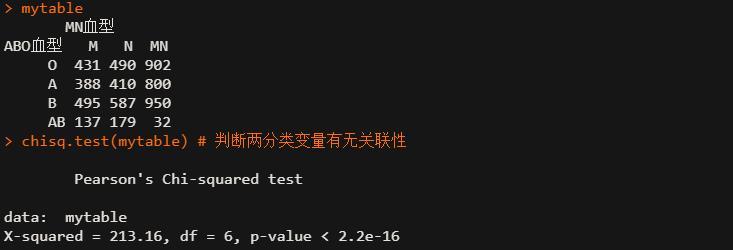
p-value < 2.2e-16,可以认为两种血型系统间有关联,可进一步计算Pearson列联系数,以分析其密切程度。
library(vcd)
assocstats(mytable) # 查看关联性的强弱
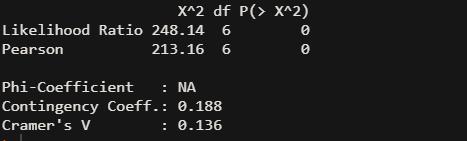
从上面可以看出,列联系数为0.188,虽然有关联性,但列联系数比较小,虽然有统计学意义,但关系不太密切。
6. 频数分布拟合优度的卡方检验
频数分布拟合优度(goodness-of-fit)检验还是使用chisq.test()函数。
chisq.test(x, # x为向量或单行/单列矩阵,参数 x 必须全部是非负整数。
p, # P是和x长度相同的概率向量,P值如果输入有负值,会返回错误信息。
# p中向量的和应为1,p不给出则向量值全部相等。
rescale.p = TRUE) # 逻辑词,为TRUE,则p将缩放成和为1的向量;为FALSE,如果和≠1,则会返回错误信息。
x <- c(10,25,15)
chisq.test(x) # chisq.test(as.table(x))等效
x <- c(82,47,20,18,22) # x为向量
p <- c(45,25,25,18,15) # p为概率
chisq.test(x, p = p) # 返回错误信息,概率总和必须为1
chisq.test(x, p = p, rescale.p = TRUE) # 运行正常以上是关于R语言分布的卡方拟合优度检验的主要内容,如果未能解决你的问题,请参考以下文章