数据结构（c++）字符串 模式匹配算法问题，对高手来说只要写一点点

Posted 2023-05-07

1、在串堆存储表示的基础上串匹配的BF算法实现 前置条件：串已存在 输入：输入子串对象ss，输入从主串第i位开始查找子串 动作：寻找子串在在主串第i位后子串第一次出现的位置。 输出：返回匹配子串的位置，否则不匹配则返回-1值。 后置条件：无 核心... 1、在串堆存储表示的基础上串匹配的BF算法实现 前置条件：串已存在 输入：输入子串对象ss，输入从主串第i位开始查找子串 动作：寻找子串在在主串第i位后子串第一次出现的位置。 输出：返回匹配子串的位置，否则不匹配则返回-1值。 后置条件：无 核心部分参考： template <class T1> int string<T1>::index(const string<T1> &T,int pos) //在S串中从pos开始查找一个与串T相同的子串 if (pos<1||pos>length) throw "pos不合法！"; int i=pos,j=1; while (i<=length &&j<=T.length) if (s[i]==T.s[j]) i++; j++; else i=i-j+2; j=1;//回溯 if (j>T.length) return (i-j+1); else return -1; 2、在串堆存储表示的基础上串匹配的KMP算法实现 前置条件：串已存在 输入：输入子串对象ss，输入从主串第i位开始查找子串 动作：寻找子串在在主串第i位后子串第一次出现的位置。 输出：返回匹配子串的位置，否则不匹配则返回-1值。 后置条件：无 核心部分参考： template <class T1> void string<T1>::getnext(const string<T1> &T,int *next) int i=0,j=-1; next[i]=-1; while(i<T.length) if(j==-1||T.s[i]==T.s[j]) //当ti=tj时，i和j分别加1，同时计算next[j]，再继续比较； //当j==-1时，则使si+1与t0比较，同上。 i++; j++; next[i]=j;//给数组next的元素赋值 else j=next[j];//不匹配，则给出新j值 //============================================================ template <class T1> int string<T1>::index(const string<T1> &T,int pos) int *next=new int[T.length]; getnext(T,next); int i=pos-1,j=0; while ( i<length && j<T.length ) if (j==-1|| s[i]==T.s[j] ) ++i;++j; //不失配则继续比较后续字符 else j=next[j]; //S的i指针不回溯，从T的k位置开始匹配 if(j>=T.length) return i-T.length+1; //子串结束，说明匹配成功位置 else return -1; 如上，对于1、2，分别写出完整的可直接运行的main函数，不一定要用模板（最好不用），这对高手来说是小菜一碟吧，复制粘贴，写个主函数，加点东西，再修改修改就好了，万分感谢，测试成功再补100分！！！ 展开 在线等，很急，测试成功，立即给分，加分！！！！！ ------------------------------------------------------- 已经不需要了，nnd，白白浪费了200分……

参考技术A 唉，还是去CSDN问吧，百度知道太水了，都是些弱智题。以后不来了。。

数据结构（C++）笔记：04.字符串与多维数组

文章目录

• 4.1 串
• • 4.1.1 串的逻辑结构
  • 4.1.2 串的存储结构
  • 模式匹配
  • • １．朴素的模式匹配算法
    • 2．改进的模式匹配算法
• 4.2 多维数组
• • 4.2.1 数组的定义
  • 4.2.2 数组的存储结构与寻址
  • 矩阵的压缩存储
  • 4.2.3 特殊矩阵的压缩存储
  • 4.2.4稀疏矩阵的压缩存储
• 参考书目：

4.1 串

4.1.1 串的逻辑结构

1. 串的定义
   串是零个或多个字符组成的有限序列，只包含空格的串称为空格串。串中所包含的字符个数称为串的长度，长度为0的串称为空串，记作 " "，一个非空串通常记作：
   $$S="s_1{s}_2\dots \dots s_n"$$
   其中，S是串名，双引号是定界符，不属于串的内容，双引号（有些书中也用单引号）引起来的部分是串值，$s_i（1\le i\le n）$是一个任意字符（可以是字母、数字或其他字符），$s_i$在串中出现的序号称为该字符在串中的位置。串中的字符数目n称为串的长度，定义中谈到“有限”是指长度n是一个有限的数值。零个字符的串称为空串（null string），它的长度为零，可以直接用两双引号“”””表示，也可以用希腊字母“$\varphi$”来表示。所谓的序列，说明串的相邻字符之间具有前驱和后继的关系。空格串，是只包含空格的串。注意它与空串的区别，空格串是有内容有长度的，而且可以不止一个空格。
   子串与主串，串中任意个数的连续字符组成的子序列称为该串的子串，相应地，包含子串的串称为主串。
   子串在主串中的位置就是子串的第一个字符在主串中的序号。
   例如：“over”、“end”、“lie”其实可以认为是“lover”、“friend”、“believe”这些单词字符串的子串。
2. 串的抽象数据类型定义

ADT String 
Data
   串中的数据元素仅由一个字符组成，相邻元素具有前驱和后继关系
Operation
       StrLength
     前置条件：串S已存在
     输入：无
     功能：求串S的长度
     输出：串S中的字符个数
     后置条件：串S不变
       StrAssign 
     前置条件：无
     输入：串T
     功能：串赋值，将T的串值赋值给串S
     输出：串S
     后置条件：串T不变
       StrConcat
     前置条件：无
     输入：串S，串T
     功能：串连接，将串T放在串S的后面连接成一个新串S
     输出：串S
     后置条件：串T不变
StrSub
     前置条件：串S已存在
     输入：位置i，长度len
     功能：求子串，返回从串S的第i个字符开始长为 len 的子串
     输出：S的一个子串
     后置条件：串S不变
StrCmp
     前置条件：无
     输入：串S，串T
     功能：串比较
     输出：若S=T，返回0；若S<T, 返回-1；若S>T, 返回1
     后置条件：串S和T不变
       StrIndex
     前置条件：串S已存在
     输入：串T
     功能：子串定位
     输出：子串T在主串S中首次出现的位置
     后置条件：串S和T不变
StrInsert
     前置条件：串S已存在
     输入：串T，位置i
     功能：串插入，将串T插入到串S 的第i个位置上
     输出：串S
     后置条件：串T不变
StrDelete
     前置条件：串S已存在
     输入：位置i，长度len
     功能：串删除，删除串S中从第i个字符开始连续len个字符
     输出：串S
     后置条件：串S的长度减少了len
StrRep
     前置条件：串S已存在
     输入：串T，串R
     功能：串替换，在串S中用串R 替换所有与串T相等的子串
     输出：串S
     后置条件：串T和R不变
endADT

串操作的特点：
串的逻辑结构和线性表很相似，不同之处在于串针对的是字符集，也就是串中的元素都是字符，哪怕串中的字符是“123”这样的数字组成，或者“2010-10-10“这样的日期组成，它们都只能理解为长度为3和长度为10的字符串，每个元素都是字符而已。
因此，对于串的基本操作与线性表是有很大差别的。线性表更关注的是单个元素的操作，比如查找一个元素，插入或删除一个元素，但串中更多的是查找子串位置、得到指定位置子串、替换子串等操作。
3. 串的比较
两个数字，很容易比较大小。2比1大，这完全正确，可是两个字符串如何比较？比如“silly”、“stupid”这样的同样表达“愚蠢的”的单词字符串，它们在计算机中的大小其实取决于它们挨个字母的前后顺序。它们的第一个字母都是“s”，我们认为不存在大小差异，而第二个字母，由于“i”字母比“t”字母要靠前，所以“i”<“t”，于是我们说“silly”<“stupid”。
事实上，串的比较是通过组成串的字符之间的编码来进行的，而字符的编码指的是字符在对应字符集中的序号。
计算机中的常用字符是使用标准的ASCII编码，更准确一点，由7位二进制数表示一个字符，总共可以表示128个字符。后来发现一些特殊符号的出现，128个不够用，于是扩展ASCII码由8位二进制数表示一个字符，总共可以表示256个字符，这已经足够满足以英语为主的语言和特殊符号进行输入、存储、输出等操作的字符需要了。可是，单我们国家就有除汉族外的满、回、藏、蒙古、维吾尔等多个少数民族文字，换作全世界估计要有成百上千种语言与文字，显然这256个字符是不够的，因此后来就有了Unicode编码，比较常用的是由16位的二进制数表示一个字符，这样总共就可以表示216个字符，约是65万多个字符，足够表示世界上所有语言的所有字符了。当然，为了和ASCII码兼容，Unicode的前256个字符与ASCII码完全相同。
所以如果我们要在C语言中比较两个串是否相等，必须是它们串的长度以及它们各个对应位置的字符都相等时，才算是相等。即给定两个串：$s=“a_1{a}_2\dots \dots a_n”$，$t=“b_1{b}_2\dots \dots b_m”$，当且仅当n=m，且$a_1=b_1，a_2=b_2，\dots ，a_n=b_n$时，我们认为s=t。
给定两个串：$s=“a_1{a}_2\dots \dots a_n”$，$t=“b_1{b}_2\dots \dots b_m”$，当满足以下条件之一时，s<t。
1.n<m，且$a_i=b_i；（i=1，2，\dots \dots ，n）$。
例如当s=“hap"，t=“happy”，就有s<t。因为t比s多出了两个字母。
2.存在某个$k\le min（m，n）$，使得$a_i=b_i；（i=1，2，\dots \dots ，k-1），a_k<b_k$。例如当s=“happen"，t=“happy”，因为两串的前4个字母均相同，而两串第5个字母（k值），字母e的ASCII码是101，而字母y的ASCII码是121，显然e<y，所以s<t。
有同学如果对这样的数学定义很不爽的话，那我再说一个字符串比较的应用。我们的英语词典，通常都是上万个单词的有序排列。就大小而言，前面的单词比后面的要小。你在查找单词的过程，其实就是在比较字符串大小的过程。

4.1.2 串的存储结构

1．串的顺序存储结构
串的顺序存储结构是用数组来存储串中的字符序列。
在串的顺序存储中，一般有三种方法表示串的长度：
⑴ 用一个变量来表示串的长度，如图3-13所示。

⑵ 在串尾存储一个不会在串中出现的特殊字符作为串的终结符，如图3-14所示。

⑶ 用数组的0号单元存放串的长度，串值从1号单元开始存放，如图3-15所示。

2．串的链接存储结构
串的链接存储结构有以下两种解决方案：
⑴ 非压缩形式。一个结点只存储一个字符，其优点是操作方便，但存储利用率低。
⑵ 压缩形式。为了提高存储空间利用率，一个结点可存储多个字符。这实质上是一种顺序与链接相结合的结构。这种存储结构增加了实现基本操作的复杂性，比如对改变串长的操作，可能涉及结点的增加与删除问题。
最后一个结点若是未被占满时，可以用“#”或其他非串值字符补全。

模式匹配

给定两个串$S="s_1{s}_2\dots s_n"和T="t_1{t}_2\dots t_m"$，在主串S中寻找子串T的过程称为模式匹配，T称为模式。如果匹配成功，返回T在S中的位置，如果匹配失败，返回0。
假设串采用顺序存储结构，串长存放在数组的0号单元，串值从1号单元开始存放。

１．朴素的模式匹配算法

BF(Brute Force)暴力匹配算法的基本思想是：从主串S的第一个字符开始和模式T的第一个字符进行比较，若相等，则继续比较两者的后续字符；否则，从主串S的第二个字符开始和模式T的第一个字符进行比较，重复上述过程，若T中的字符全部比较完毕，则说明本趟匹配成功；否则匹配失败。

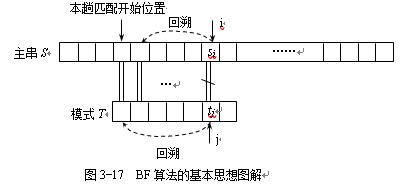
设串S长度为n，串T长度为m，在匹配成功的情况下，考虑两种极端情况：
⑴ 在最好情况下，每趟不成功的匹配都发生在串T的第一个字符。
即最好情况下的时间复杂度是O(n+m)。
分析一下，最好的情况是什么？那就是一开始就区配成功，比如“googlegood”中去找“google”，时间复杂度为O(1)。稍差一些，如果像刚才例子中第二、三、四位一样，每次都是首字母就不匹配，那么对T串的循环就不必进行了，比如“abcdefgooge”中去找“google”。那么时间复杂度为O（n+m），其中n为主串长度，m为要匹配的子串长度。根据等概率原则，平均是（n+m）/2次查找，时间复杂度为O（n+m）。
⑵ 在最坏情况下，每趟不成功的匹配都发生在串T的最后一个字符。
一般情况下，m<< n，因此最坏情况下的时间复杂度是O(n×m)。
那么最坏的情况又是什么？就是每次不成功的匹配都发生在串T的最后一个字符。举一个很极端的例子。主串为S=“00000000000000000000000000000000000000000000000001”，而要匹配的子串为T=“0000000001”，前者是有49个“0”和1个“1”的主串，后者是9个“0”和1个“1”的子串。在匹配时，每次都得将T中字符循环到最后一位才发现：哦，原来它们是不匹配的。这样等于T串需要在S串的前40个位置都需要判断10次，并得出不匹配的结论，如图5-6-6所示。直到最后第41个位置，因为全部匹配相等，所以不需要再继续进行下去，如图5-6-7所示。如果最终没有可匹配的子串，比如是T=“0000000002”，到了第41位置判断不匹配后同样不需要继续比对下去。因此最坏情况的时间复杂度为$O((n-m+1)\ast m)$。

2．改进的模式匹配算法

这里感觉C++版本和大话数据结构版本的描述有点不一样。。。。先记下来
用next[j]表示$t_j$对应的k值（1≤j≤m），其定义如下：
$$\{\begin{array}{c}-1j=1（大话数据结构这里用的是0）\\ maxk|1\le k＜j且"t_1{t}_2\dots 以上是关于数据结构（c++）字符串\; 模式匹配算法问题，对高手来说只要写一点点的主要内容，如果未能解决你的问题，请参考以下文章\end{array}$$

数据结构关于串的KMP算法的理解高手请进

数据结构第四章学习小结

kmp算法字符串匹配算法

数据结构（C++）笔记：04.字符串与多维数组

C++ 算法进阶系列之从 Brute Force 到 KMP 字符串匹配算法的优化之路

数据结构与算法——字符串匹配问题(KMP算法)