每日一题_191110

Posted 2020-11-21 math521

阿波罗尼斯是古希腊著名数学家,与欧几里得,阿基米德被成为亚历山大时期的数学三巨匠,他对圆锥曲线有深刻而系统的研究,主要研究成果集中在他的代表作《圆锥曲线论》一书,阿波罗尼斯圆是他的研究成果之一,指的是(:)已知动点(M)与两定点(A,B)距离之比为(lambda) ((lambda>0),(lambda eq 1)),那么点(M)的轨迹就是阿波罗尼斯圆.如动点(M)与两定点 $ Aleft(dfrac{9}{5},0 ight)$ ,(B(5,0))的距离之比为 (dfrac35) 时的阿波罗尼斯圆为(x^2+y^2=9).下面,我们来研究与此相关的一个问题.已知圆(O:x^2+y^2=1)上的动点(M)和定点(Aleft(-dfrac{1}{2},0 ight)), (B(1,1)) 则 (2|MA|+|MB|) 的最小值为((qquad))
(mathrm{A}.sqrt{6}) (qquadmathrm{B}.sqrt{7}) (qquadmathrm{C}.sqrt{10}) (qquadmathrm{D}.sqrt{11})

解析:
记点(C(-2,0)),则(C,A)两点是关于圆(O)的对反演点,

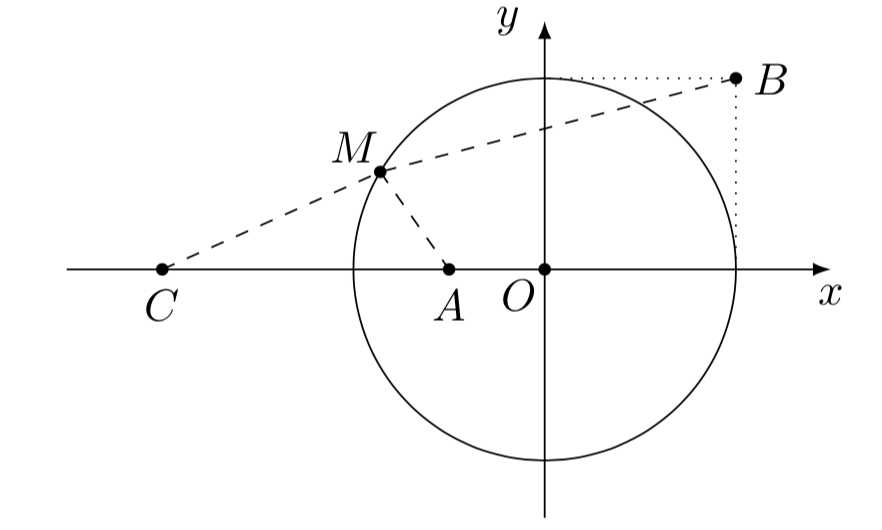
且恒有[|MC|:|MA|=2:1.]因此[ 2|MA|+|MB|=|MC|+|MB|geqslant |BC|=sqrt{10}.]因此当(M)位于线段(BC)上时,所求表达式取得最小值(sqrt{10}).选项( m C)正确.