主元分析法是啥?
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了主元分析法是啥?相关的知识,希望对你有一定的参考价值。
简介主元分析法(PCA)是目前基于多元统计过程控制的故障诊断技术的核心,是基于原始数据空间,通过构造一组新的潜隐变量来降低原始数据空间的维数,再从新的映射空间抽取主要变化信息,提取统计特征,从而构成对原始数据空间特性的理解。新的映射空间的变量由原始数据变量的线性组合构成,从而大大降低了投影空间的维数。由于投影空间统计特征向量彼此正交,则消除了变量间的关联性,简化了原始过程特性分析的复杂程度。
编辑本段
基本思路
主元分析法的基本思路是:寻找一组新变量来代替原变量,新变量是原变量的线性组合。从优化的角度看,新变量的个数要比原变量少,并且最大限度地携带原变量的有用信息,且新变量之间互不相关。其内容包括主元的定义和获取,以及通过主元的数据重构。
编辑本段
定义
假设一个要研究的系统仅包含两个变量 x1 , x2 。将两个变量的样本点表示在一个平面图上,可以看出所有的样本点集中在一个扁型的椭圆区域内。因为样本点之间的差异显然是由于 x1 , x2 的变化而引起的。我们可以看出在沿着椭圆横轴的方向上( y1 )的变动较大,而纵轴方向上( y2 )的变动较小。这说明了样本点的主要变动都体现在横轴方向上,比如 85%以上,那么这时就可以将 y 2忽略而只考虑y1 。这样两个变量就可以简化为一个变量了。我们称 y1 , y 2分别为 x1 , x2 的第一主元和第二主元。一般情况下,如果样本有 p 个变量,若样本之间的差异能由 p 个变量的 K 个(K<p)个主元成分来概括,那么就能用 K 个主元来代替 p 个变量。
编辑本段
主元得分向量
主元分析中数据总体的协方差阵往往是未知的,这需要利用过程的正常运行数据进行估计。假设采集得到过程数据样本为 X ∈ R n ×p,其中 n是样本的数量,p 为过程变量的个数。为了避免变量的不同量纲的影响,需首先对数据进行标准化处理,即将各个变量转化为均值为 0,方差为 1 的数据。
编辑本段
确定方法
目前在主元个数的选择上,有两种比较普遍的方法,一种使主元回归检验法,一种是主元贡献率累积和百分比法(CPV)。
编辑本段
检测统计量
检测统计
从统计的角度讲,要检测数据中是否包含过程的故障信息,可以通过建立统计量进行假设检验,判断过程数据是否背离了主元模型。通常的方法是主元子空间建立 Hotelling T2 统计量进行统计检验;在残差子空间中建立 Q 统计量进行统计检测。
百度百科上有的
http://baike.baidu.com/view/3656019.htm 参考技术A 主元分析法(PCA)是目前基于多元统计过程控制的故障诊断技术的核心,是基于原始数据空间,通过构造一组新的潜隐变量来降低原始数据空间的维数,再从新的映射空间抽取主要变化信息,提取统计特征,从而构成对原始数据空间特性的理解。
主元分析法的基本思路是:寻找一组新变量来代替原变量,新变量是原变量的线性组合。从优化的角度看,新变量的个数要比原变量少,并且最大限度地携带原变量的有用信息,且新变量之间互不相关。其内容包括主元的定义和获取,以及通过主元的数据重构。
《数值分析》-- 高斯消去法与矩阵三角分解法(LU分解)
文章目录
引言
- 研究数值解法的必要性


- 线性代数方程组的常用解法
- 直接法
只包含有限次四则运算。在计算过程中不发生舍入误差的假定下,计算结果就是原方程组的精确解。(适用于小规模的n阶稠密线性方程组) - 迭代法
从解的某个近似值出发,通过构造一个无穷序列去逼近精确解的方法(一般有限步内得不到精确解)。实现这一极限过程每一步的结果是把前一步所得的结果施行相同的演算步骤得到的。(适用于大规模的n阶稀疏线性方程组)
Remark:由于运算过程中舍入误差的存在,实际上
直接方法得到的解也是方程组的近似解。
一、预备知识
1.1 矩阵基本运算和和行列式

1.2 矩阵的特征值和谱半径

设A是n阶方阵,如果数λ和n维非零列向量x使关系式Ax=λx成立,那么这样的数λ称为矩阵A特征值,非零向量x称为A的对应于特征值λ的特征向量。
-
特征值性质
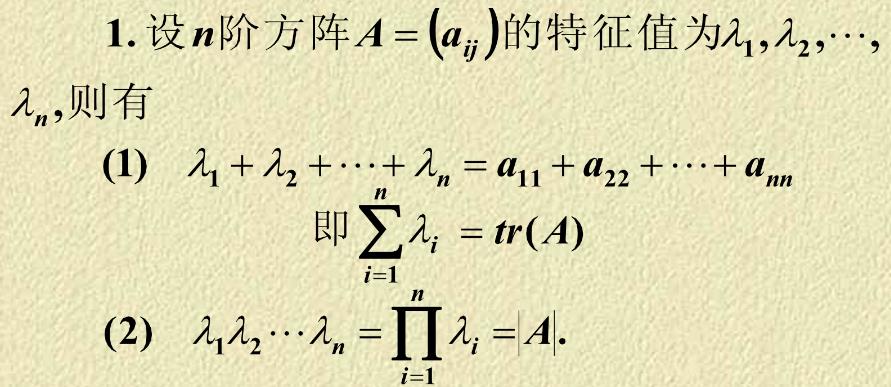
t r ( A ) tr(A) tr(A)为A 的迹。

-
注意

-
谱半径
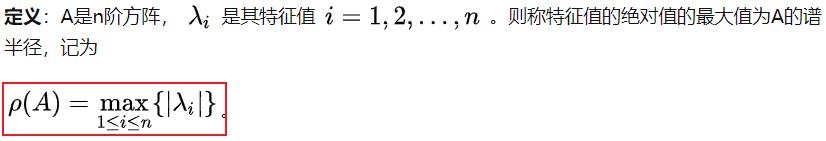
习题
1.3 特殊矩阵

- 对称正定矩阵

二、Gauss消去法
- 方程组的矩阵表示

高斯消元的基本思想:将矩阵A的下三角部分消为零,即化为上三角形
2.1 不消主元的Gauss消去法
首先将方程组
Ax=b化为上三角方程组,此过程称为消去过程,再求解上三角方程组,此过程称为回代过程.
例.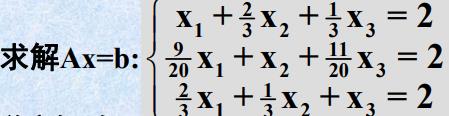


总结:Gauss消去法解Ax=b分两步:消元、回代.
- 不消主元的Gauss消去法
将方程组Ax=b的系数矩阵与右端项合并为:

第一步:

第二步:

第k步:

第n-1步:


回代:

- 定理


2.2 高斯主元素消去法
在计算过程中的舍入误差增大能得到控制,该方法就是稳定的。
小主元是不稳定的根源,这就需要采用“选主元素”技术,即选取绝对值最大的元素作为主元。
1. Gauss列主元消去法
a
k
k
(
k
)
a_kk^(k)
akk(k) 称为第k步的主元

- Gauss列主元消去法:
第一步:在第一列中选取最大值的元素,并将该行 a i , 1 a_i,1 ai,1与第一行 a 1 , 1 a_1,1 a1,1进行交换。(若该列中第一行 a 1 , 1 a_1,1 a1,1最大,无需交换)


第k步:设第 步将增广矩阵(A,b)已化为


结论:当 k k k从 1 1 1变化到 n − 1 n-1 n−1时, ( A , b ) (A,b) (A,b)成为上三角形式,再用回代公式求 x x x.
例. 用Gauss列主元解方程组

2. Gauss全主元消去法
概念不好理解,直接上例题+解析。
例. 

通常用列主元消去法。
三、矩阵的三角分解法
3.1 用直接三角分解法求解方程组
- 高斯消元与LU分解的等价性
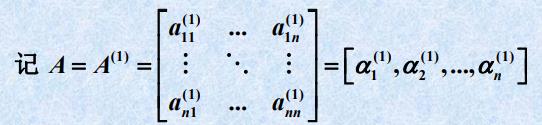
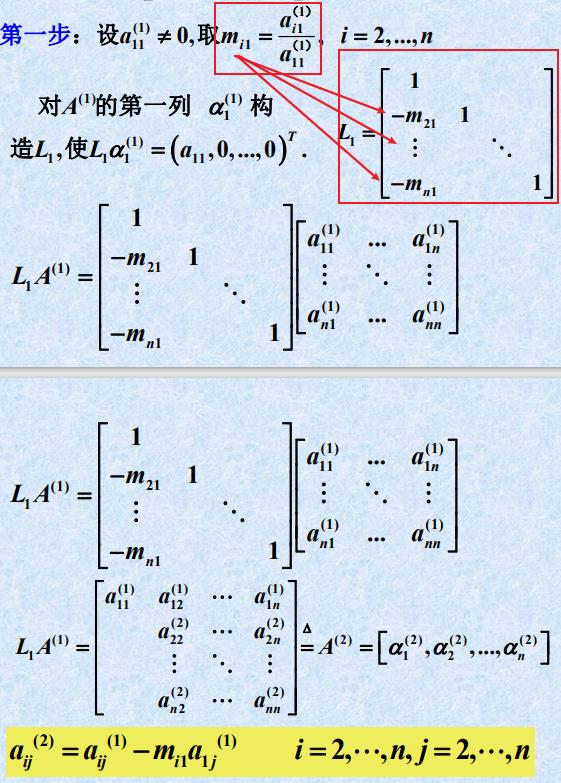
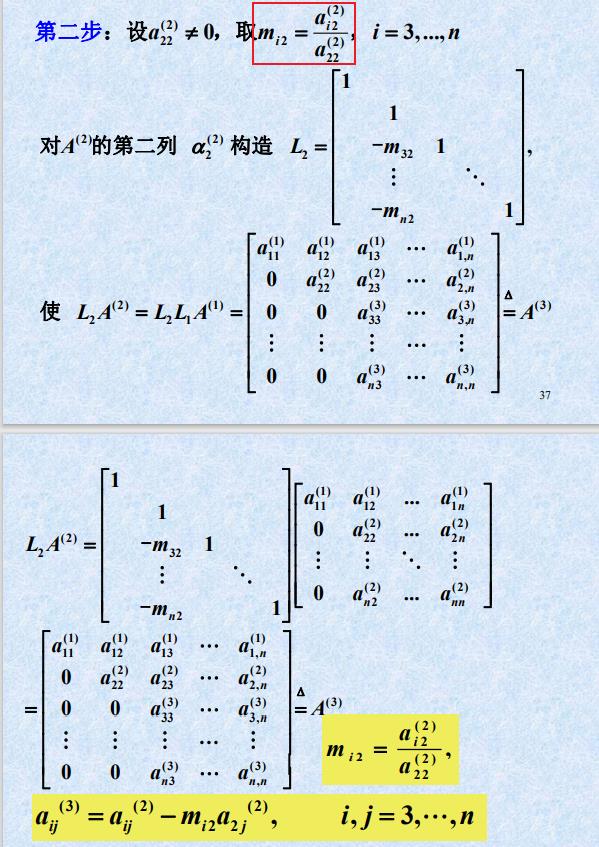



- L与U ⭐⭐
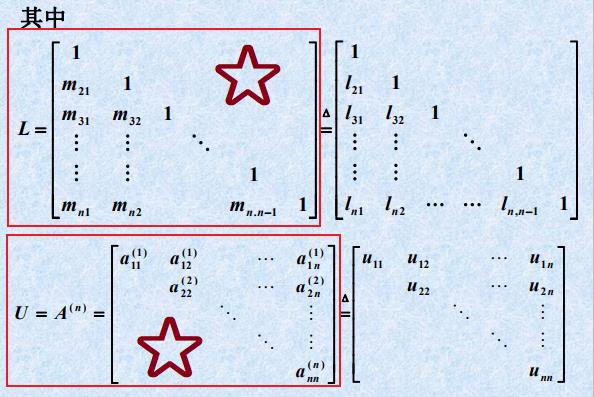
- 矩阵三角分解的基本定理


3.2 Doolittle分解法(杜利特尔)
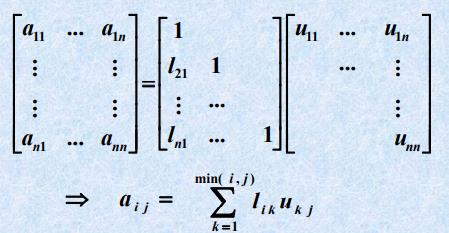
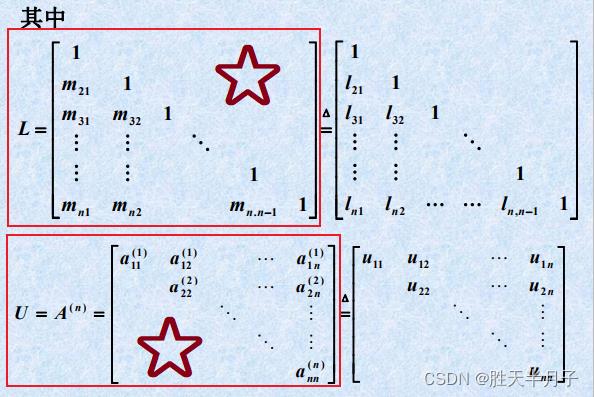
- 一般计算公式⭐


习题
题目
- 例题
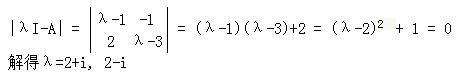
谱半径,就是特征值绝对值(复数取模)中的最大值,先求特征值。再取模,分别得到√5,√5,因此谱半径是√5。

- 例题
以上是关于主元分析法是啥?的主要内容,如果未能解决你的问题,请参考以下文章




