合并果子2之蚂蚁搬沙 贪心

Posted 2020-11-21 nlyzl

 

 

本人水平有限，题解不到为处，请多多谅解

 

本蒟蒻谢谢大家观看

 

 

题目：

1552: 合并果子2之蚂蚁搬沙

Time Limit: 1 Sec  Memory Limit: 128 MB
Submit: 353  Solved: 158
[Submit][Status][Web Board]

Description

山谷中住着一个巨大的蚂蚁王国，蚁穴外有一个整洁的广场，天气晴好时蚁群常在那里举行各种活动。这天夜里，天降果子尘，第2天，广场上堆满了大大小小的果子堆，蚁哨出去数了数共有n堆，蚁后要求她的臣民将广场上的果子堆清理掉。具体办法是：每次可以把广场上的任意k堆果子合并成一堆，重复进行直至所有的果子堆最终合并成一堆。规定（1）：2≤k≤m，m由蚁后指定，（2）：每次合并k堆果子的代价是这k堆果子子的重量和。 
你的任务是，对给定的n和m，计算出将n堆果子最终合并成1堆的最小总代价。 
例如，广场上有7堆果子，其重量分别为45，13，12，16，9，5，22。当m=3时，这些果子堆合并成一堆的最小总代价为199。当m=5时，这些果子堆合并成一堆的最小总代价为148。

Input

包含n+2个整数（n≤100000），其中第一行2个正整数，分别表示n堆果子和每次合并时可以合并的最大堆数m，从第二行开始有n个数，表示n堆果子的重量（1～500），数与数之间用空格隔开。

Output

只包含一个正整数，表示将n堆果子合并成1堆所需的最小总代价。

Sample Input

7 3
45 13 12 16 9 5 22

Sample Output

199 

HINT

 

Source

合并果子类的题目都可以看成是一个完全k叉树。

为什么呢？

先拿样例来说

 

 

 

 

 

 

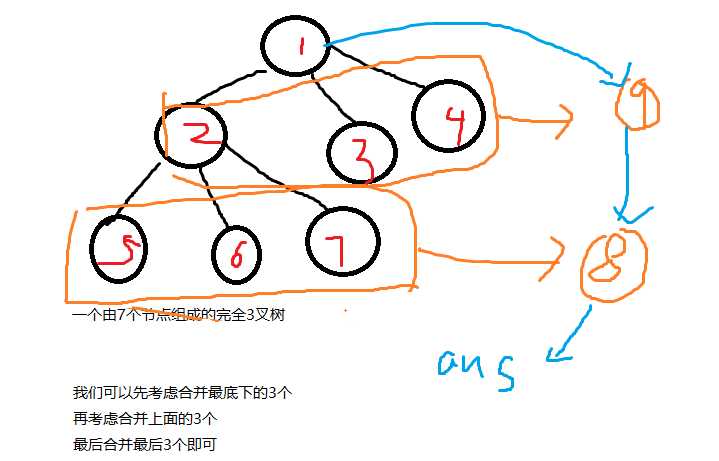
这样就可以刚好合并完所有的节点

 

那如果无法刚好合并完，怎么办？

 

这时我们可以多加入几个节点，使其变成完全k叉树，

 

注意：这里加入的几个点权值必须为0。

 

这样就解决了无法合并的问题。

 

那如何算出到底要多加几个节点呢？

 

计算方式：

 

因为每次可以合并m堆，所以可以合并成（n/m）堆完整的，并且还剩下（n%m）堆，

 

n堆就等同于(n/m)+(n%m)堆,

 

一直进行此运算，直到（n<=m）时，n距离完整的m堆还差（m-n）堆，

 

即（m-n)  就是添0的个数。

 

最后我们就可以用一个小根堆来维护，不断的加入最小值，其解最后一定最优。

 

code:

 1 #include<bits/stdc++.h>
 2 #pragma GCC optimize(3)
 3 
 4 using namespace std;
 5 int n,k,nn,add,ans;
 6 priority_queue<int,vector<int>,greater<int> >q;//小根堆 
 7 void inint(){
 8     freopen("sand.in","r",stdin);
 9     freopen("sand.out","w",stdout);
10 }
11 inline int read(){
12     int x=0,f=1;char ch=getchar();
13     while(!isdigit(ch)){if(ch==‘-‘)f=-1;ch=getchar();}
14     while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
15     return x*f;
16 }
17 inline void write(int x)
18 {
19     if(x<0)x=-x,putchar(‘-‘);
20     if(x>9)write(x/10);
21     putchar(x%10+‘0‘);
22 }
23 int main()
24 {
25     //inint();
26     n=read(),k=read();
27     for(int i=1,y;i<=n;i++){
28         y=read();
29         q.push(y);
30     }
31     nn=n;
32     while(1){
33         int c=nn/k;
34         int mod=nn%k;
35         nn=c+mod;
36         if(nn<=k){
37             add=k-nn;//加入add个0 
38             break;
39         }
40     }
41     for(int i=1;i<=add;i++){
42         q.push(0);
43     }
44     while(!q.empty()){
45         int x=0;
46         for(int i=1;i<=k;i++){
47             x+=q.top();
48             q.pop();
49         }
50         ans+=x;
51         if(q.empty()){
52             printf("%d
",ans);//注意：一定要这样写，如果把ans最后统计的话，会导致死循环 
53             return 0;
54         }
55         q.push(x);
56     }
57     return 0;
58 }