嵌入式与神经网络（二）：CNN卷积层

Posted 2023-05-06

参考技术A 姓名：王央京    学号：18050100052   学院：电子工程学院

转自：https://blog.csdn.net/qq_25762497/article/details/51052861

【嵌牛导读】本文具体介绍了CNN中的卷积层

【嵌牛鼻子】卷积层

【嵌牛提问】在初步了解之后，对CNN中的卷积层进行具体介绍

【嵌牛正文】

局部感知（Local Connectivity）

普通神经网络把输入层和隐含层进行“全连接(Full Connected)“的设计。从计算的角度来讲，相对较小的图像从整幅图像中计算特征是可行的。但是，如果是更大的图像（如 96x96 的图像），要通过这种全联通网络的这种方法来学习整幅图像上的特征，从计算角度而言，将变得非常耗时。你需要设计 10 的 4 次方（=10000）个输入单元，假设你要学习 100 个特征，那么就有 10 的 6 次方个参数需要去学习。与 28x28 的小块图像相比较， 96x96 的图像使用前向输送或者后向传导的计算方式，计算过程也会慢 100倍。

卷积层解决这类问题的一种简单方法是对隐含单元和输入单元间的连接加以限制：每个隐含单元仅仅只能连接输入单元的一部分。例如，每个隐含单元仅仅连接输入图像的一小片相邻区域。（对于不同于图像输入的输入形式，也会有一些特别的连接到单隐含层的输入信号“连接区域”选择方式。如音频作为一种信号输入方式，一个隐含单元所需要连接的输入单元的子集，可能仅仅是一段音频输入所对应的某个时间段上的信号。)

每个隐含单元连接的输入区域大小叫r神经元的感受野(receptive field)。

由于卷积层的神经元也是三维的，所以也具有深度。卷积层的参数包含一系列过滤器（filter），每个过滤器训练一个深度，有几个过滤器输出单元就具有多少深度。

具体如下图所示，样例输入单元大小是32×32×3, 输出单元的深度是5, 对于输出单元不同深度的同一位置，与输入图片连接的区域是相同的，但是参数（过滤器）不同。

虽然每个输出单元只是连接输入的一部分，但是值的计算方法是没有变的，都是权重和输入的点积，然后加上偏置，这点与普通神经网络是一样的，如下图所示：

空间排列（Spatial arrangement）

一个输出单元的大小有以下三个量控制：depth, stride 和 zero-padding。

深度(depth) : 顾名思义，它控制输出单元的深度，也就是filter的个数，连接同一块区域的神经元个数。又名：depth column

步幅(stride)：它控制在同一深度的相邻两个隐含单元，与他们相连接的输入区域的距离。如果步幅很小（比如 stride = 1）的话，相邻隐含单元的输入区域的重叠部分会很多; 步幅很大则重叠区域变少。

补零(zero-padding) ： 我们可以通过在输入单元周围补零来改变输入单元整体大小，从而控制输出单元的空间大小。

我们先定义几个符号：

W : 输入单元的大小（宽或高）

F : 感受野(receptive field)

S : 步幅（stride）

P : 补零（zero-padding)的数量

K : 深度，输出单元的深度

则可以用以下公式计算一个维度（宽或高）内一个输出单元里可以有几个隐藏单元：

如果计算结果不是一个整数，则说明现有参数不能正好适合输入，步幅（stride）设置的不合适，或者需要补零，证明略，下面用一个例子来说明一下。

这是一个一维的例子，左边模型输入单元有5个，即W=5, 边界各补了一个零，即P=1，步幅是1， 即S=1，感受野是3，因为每个输出隐藏单元连接3个输入单元，即F=3，根据上面公式可以计算出输出隐藏单元的个数是5，与图示吻合。右边那个模型是把步幅变为2，其余不变，可以算出输出大小为3，也与图示吻合。若把步幅改为3，则公式不能整除，说明步幅为3不能恰好吻合输入单元大小。另外，网络的权重在图的右上角，计算方法和普通神经网路一样。

参数共享(Parameter Sharing)

应用参数共享可以大量减少参数数量，参数共享基于一个假设：如果图像中的一点（x1, y1）包含的特征很重要，那么它应该和图像中的另一点（x2, y2）一样重要。换种说法，我们把同一深度的平面叫做深度切片(depth slice)，那么同一个切片应该共享同一组权重和偏置。我们仍然可以使用梯度下降的方法来学习这些权值，只需要对原始算法做一些小的改动， 这里共享权值的梯度是所有共享参数的梯度的总和。

我们不禁会问为什么要权重共享呢？一方面，重复单元能够对特征进行识别，而不考虑它在可视域中的位置。另一方面，权值共享使得我们能更有效的进行特征抽取，因为它极大的减少了需要学习的自由变量的个数。通过控制模型的规模，卷积网络对视觉问题可以具有很好的泛化能力。

卷积（Convolution）

如果应用参数共享的话，实际上每一层计算的操作就是输入层和权重的卷积！这也就是卷积神经网络名字的由来。

先抛开卷积这个概念不管。为简便起见，考虑一个大小为5×5的图像，和一个3×3的卷积核。这种情况下，卷积核实际上有9个神经元，他们的输出又组成一个3×3的矩阵，称为特征图。第一个神经元连接到图像的第一个3×3的局部，第二个神经元则连接到第二个局部。具体如下图所示。

图的上方是第一个神经元的输出，下方是第二个神经元的输出。每个神经元的运算依旧是

现在我们回忆一下离散卷积运算。假设有二维离散函数 f(x,y) , g(x,y)， 那么它们的卷积定义为

上面例子中的9个神经元均完成输出后，实际上等价于图像和卷积核的卷积操作。

理解CNN卷积层与池化层计算

概述

深度学习中CNN网络是核心，对CNN网络来说卷积层与池化层的计算至关重要，不同的步长、填充方式、卷积核大小、池化层策略等都会对最终输出模型与参数、计算复杂度产生重要影响，本文将从卷积层与池化层计算这些相关参数出发，演示一下不同步长、填充方式、卷积核大小计算结果差异。

一：卷积层

卷积神经网络(CNN)第一次提出是在1997年，杨乐春（LeNet）大神的一篇关于数字OCR识别的论文，在2012年的ImageNet竞赛中CNN网络成功击败其它非DNN模型算法，从此获得学术界的关注与工业界的兴趣。毫无疑问学习深度学习必须要学习CNN网络，学习CNN就必须明白卷积层，池化层等这些基础各层，以及它们的参数意义，从本质上来说，图像卷积都是离散卷积，图像数据一般都是多维度数据（至少两维），离散卷积本质上是线性变换、具有稀疏与参数重用特征即相同参数可以应用输入图像的不同小分块，假设有3x3离散卷积核如下：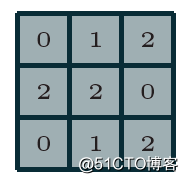

假设有

• 5x5的图像输入块
• 步长为1(strides=1)
• 填充方式为VALID(Padding=VALID)
• 卷积核大小filter size=3x3

则它们的计算过程与输出如下

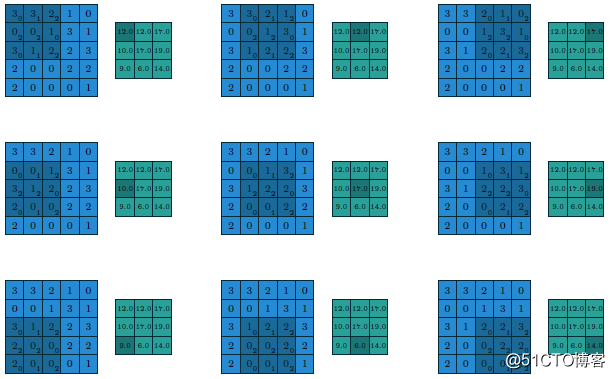
假设这个时候我们修改步长为2、填充方式为SAME，卷积核大小不变(strides=2 Padding=SAME filter size=3x3)，则计算过程与输出变为如下：

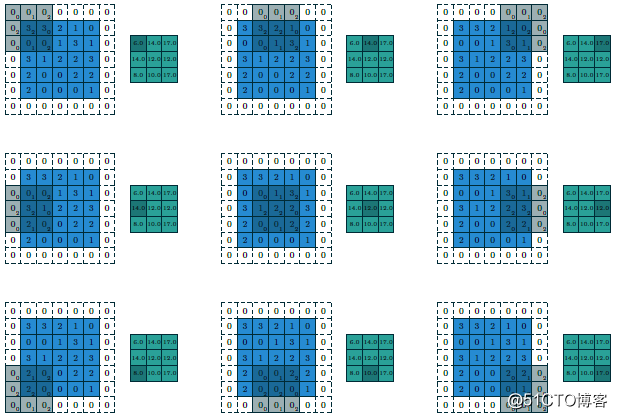
最终输出得到的结果我们可以称为featuremap，CNN的深度多数时候是指featuremap的个数，对多维度的输入图像计算多个卷积核，得到多个featuremap输出叠加，显示如下：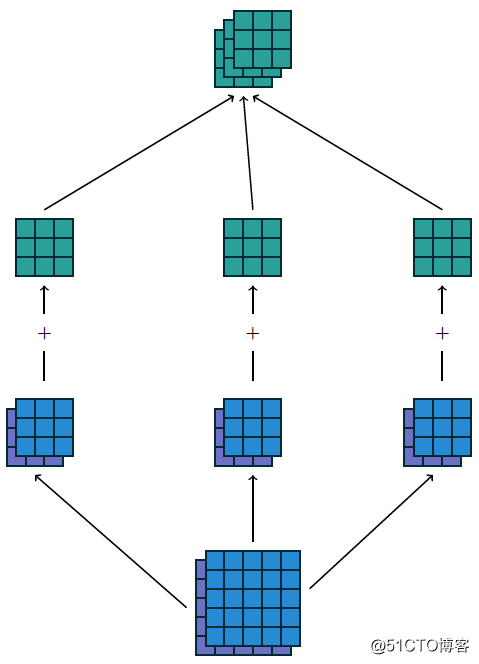

上述输入为5x5x2，使用卷积核3x3，输出3x3x3，填充方式为VALID，计算如果填充方式改为SAME则输出为5x5x3。可以看出填充方式对输出结果的影响。

二：小卷积核VS大卷积核

在AlexNet中有有11x11的卷积核与5x5的卷积核，但是在VGG网络中因为层数增加，卷积核都变成3x3与1x1的大小啦，这样的好处是可以减少训练时候的计算量，有利于降低总的参数数目。关于如何把大卷积核替换为小卷积核，本质上有两种方法。

1.将二维卷积差分为两个连续一维卷积

二维卷积都可以拆分为两个一维的卷积，这个是有数学依据的，所以11x11的卷积可以转换为1x11与11x1两个连续的卷积核计算，总的运算次数：

• 11x11 = 121次
• 1x11+ 11x1 = 22次

2.将大二维卷积用多个连续小二维卷积替代

可见把大的二维卷积核在计算环节改成两个连续的小卷积核可以极大降低计算次数、减少计算复杂度。同样大的二维卷积核还可以通过几个小的二维卷积核替代得到。比如：5x5的卷积，我们可以通过两个连续的3x3的卷积替代，比较计算次数

• 5x5= 25次
• 3x3+ 3x3=18次

三：池化层

在CNN网络中卷积池之后会跟上一个池化层，池化层的作用是提取局部均值与最大值，根据计算出来的值不一样就分为均值池化层与最大值池化层，一般常见的多为最大值池化层。池化的时候同样需要提供filter的大小、步长、下面就是3x3步长为1的filter在5x5的输入图像上均值池化计算过程与输出结果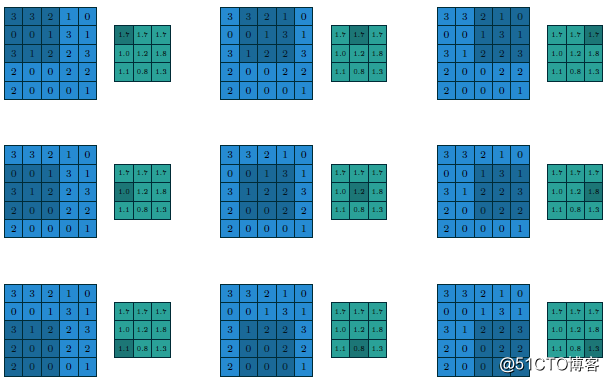

改用最大值做池化的过程与结果如下：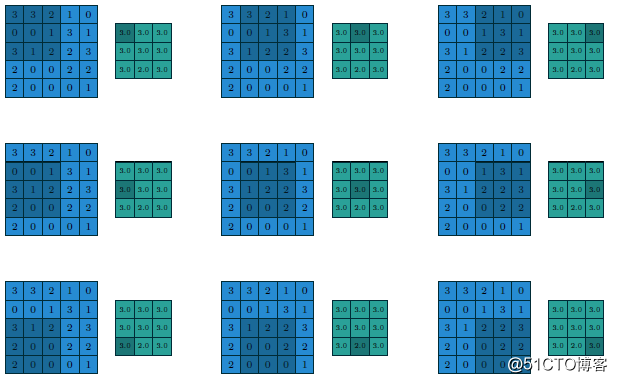

天下难事，
必作于易；
天下大事，
必作于细！

---