第k短路

Posted 2020-11-21 hh13579

问题描述

给定一个有(n)个结点,(m)条边的有向图，求从s到t的所有不同路径中的第k短路径的长度。此问题可以用于城市导航(一般会给出几条路径让人选择)

(A*)算法

背景

(A*) 算法不仅在解决路径搜索相关的应用中十分普遍，包括网络路由算法、机器人探路、人工智能、游戏设计等,而且在(GIS)的交通路线导航、路径分析领域应用更加广泛。它是人工智能领域的一种图搜索策略，采用了启发式函数对搜索过程中产生的分支进行评估，以选择最佳的分支进行搜索。它实现关键在于建立一个合适的估价函数。估价函数构造得越准确，则搜索策略越优。

如何用(A*)算法求第k短路

(A*)算法定义了一个对当前状态(x)的估价函数(f(x)=g(x)+h(x))，其中(g(x))为从初始状态到达当前状态的实际代价,(h(x))为从当前状态到达目标状态的最佳路径的估计代价。每次取出(f(x))优的状态(x)，扩展其所有子状态，可以用优先队列来维护这个值。
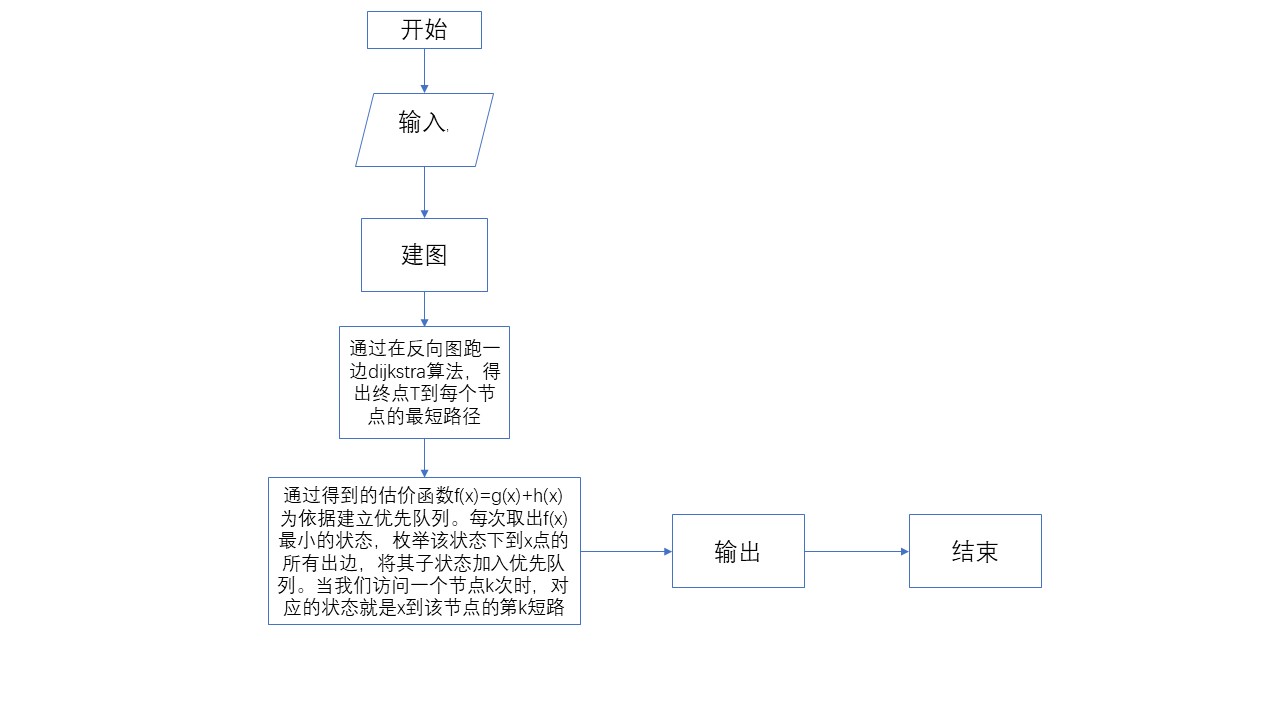
在求解(k)短路问题时，令(h(x))为从当前结点到达终点(t)的最短路径长度。可以通过在反向图上对结点(t)跑单源最短路预处理出对每个结点的这个值。
由于设计的距离函数和估价函数，对于每个状态需要记录两个值，为当前到达的结点(x)和已经走过的距离(g(x))，将这种状态记为((x,g(x)))。
开始我们将初始状态((s,0))加入优先队列。每次我们取出估价函数(f(x)=g(x)+h(x))最小的一个状态，枚举该状态到达的结点(x)的所有出边，将对应的子状态加入优先队列。当我们访问到一个结点第(k)次时，对应的状态的(g(x))就是从(x)到该结点的第(k)短路。

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
const int maxn = 5010;
const int maxm = 400010;
const int inf = 2e9;
int n, m, s, t, k, u, v, ww, H[maxn], cnt[maxn];
int cur, h[maxn], nxt[maxm], p[maxm], w[maxm];
int cur1, h1[maxn], nxt1[maxm], p1[maxm], w1[maxm];
bool tf[maxn];
void add_edge(int x, int y, double z) {
  cur++;
  nxt[cur] = h[x];
  h[x] = cur;
  p[cur] = y;
  w[cur] = z;
}
void add_edge1(int x, int y, double z) {
  cur1++;
  nxt1[cur1] = h1[x];
  h1[x] = cur1;
  p1[cur1] = y;
  w1[cur1] = z;
}
struct node {
  int x, v;
  bool operator<(node a) const { return v + H[x] > a.v + H[a.x]; }
};
priority_queue<node> q;
struct node2 {
  int x, v;
  bool operator<(node2 a) const { return v > a.v; }
} x;
priority_queue<node2> Q;
int main() {
  scanf("%d%d%d%d%d", &n, &m, &s, &t, &k);
  while (m--) {
    scanf("%d%d%d", &u, &v, &ww);
    add_edge(u, v, ww);
    add_edge1(v, u, ww);
  }
  for (int i = 1; i <= n; i++) H[i] = inf;
  Q.push({t, 0});
  while (!Q.empty()) {
    x = Q.top();
    Q.pop();
    if (tf[x.x]) continue;
    tf[x.x] = true;
    H[x.x] = x.v;
    for (int j = h1[x.x]; j; j = nxt1[j]) Q.push({p1[j], x.v + w1[j]});
  }
  q.push({s, 0});
  while (!q.empty()) {
    node x = q.top();
    q.pop();
    cnt[x.x]++;
    if (x.x == t && cnt[x.x] == k) {
      printf("%d
", x.v);
      return 0;
    }
    if (cnt[x.x] > k) continue;
    for (int j = h[x.x]; j; j = nxt[j]) q.push({p[j], x.v + w[j]});
  }
  printf("-1
");
  return 0;
}