递归之深度优先搜索
Posted guohaoblog
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了递归之深度优先搜索相关的知识,希望对你有一定的参考价值。
递归的思想在写程序中运用较为广泛,看视很复杂的问题,通常通过递归思想找出“递归结构”,分解成重复的小步骤即可解决,但是递归的思想有时并不好理解(大佬,悟性高的忽略)。本文通过介绍全排序例子介绍递归思想,最后给出前一次博客写的”坑爹的奥数“问题进行递归优化,给出执行时间。
一、问题描述:假如有编号为1、2、3的3张扑克牌和编号为1、2、3的3个盒子。现在需要将这3张扑克牌分别放到3个盒子里面,并且每个盒子有且只有一张扑克牌。那么一共有多少种不同的放法呢?
当有n个数字n个盒子(每个数字取值1~n之间且不重复),那么有多少种不同的放法呢?
输入:n ------- 表示n个盒子
输出:全排序 和 排序总数
二、代码示例(带有详细注释)
1 #include <stdio.h> 2 3 int a[10]={0},book[10]={0},n; 4 5 void dfs(int step) // step表示现在站在第几个盒子面前 6 { 7 int i; 8 if(step==n+1) // 如果站在第n+1个盒子面前,则表示前n个盒子已经放好扑克牌 9 { 10 // 输出一种排序(1~n号盒子的扑克牌编号) 11 for(i=1;i<=n;++i) 12 printf("%d",a[i]); 13 printf(" "); 14 } 15 16 // 此时站在第step个盒子面前,应该放哪张牌呢? 17 // 按照1,2,3,。。。,n的顺序一一尝试 18 for(i=1;i<=n;++i) 19 { 20 // 判断扑克牌i是否还在手上 21 if(book[i]==0) // book[i]等于0表示i号扑克牌在手上 22 { 23 // 开始尝试使用扑克牌 24 a[step] = i; // 将i号扑克牌放入到第step个盒子中 25 book[i] = 1; // 将book[i]设为1,表示i号扑克牌已经不再手上 26 27 // 第step个盒子已经放好扑克牌没接下来需要走到下一个盒子面前 28 dfs(step+1); // 这里通过函数的递归调用来实现(自己调用自己) 29 book[i] = 0; // 这是非常关键的一步,一定要将刚才尝试的扑克牌收回,才能进行下一次尝试 30 } 31 } 32 return; 33 } 34 35 /* 36 深度优先搜索的基本模型 37 void dfs(int step) 38 { 39 判断边界 40 尝试每一种可能 41 for(i=1;i<=n;++i) 42 { 43 继续下一步 dfs(step+1); 44 } 45 返回 return ; 46 } 47 */ 48 49 int main() 50 { 51 printf("请输入1~9之间的整数 "); 52 scanf("%d",&n); // 输入的时候需要主要n为1~9之间的整数 53 dfs(1); // 首先站在1号小盒子面前 54 printf(" "); 55 return 0; 56 }
运行结果如下:
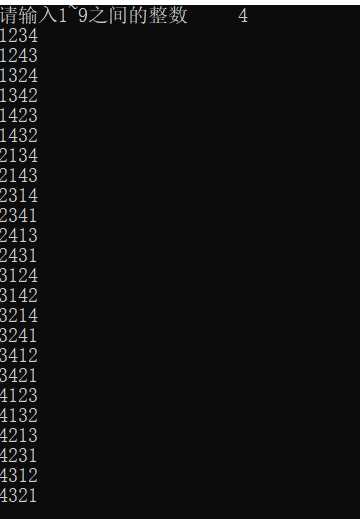
核心代码不超过20行,也就是递归的思想 ,模板已给出。关于递归思想可以看《程序员数学》第六章,个人感觉写的很好。下面介绍前面介绍的“坑爹的奥数问题”给出递归代码并与其他算法比较
问题描述:https://www.cnblogs.com/guohaoblog/p/9255706.html
方法一:枚举法(嵌套多重循环)
1 #include <stdio.h> 2 #include <time.h> 3 /* 4 有9个方格 三个一组构成一个数字,两个数相加等于第三个数,这9个数从1~9中选取 5 且每个数字只能使用一次使得等式成立 例如 173+286=459 6 请问一种有多少中合理的组合? 7 */ 8 9 int main(int argc, char *argv[]) 10 { 11 int a[10],i,total=0; // a[1]~a[9] 表示这9个数 12 double start,end; 13 start = clock(); 14 for(a[1]=1;a[1]<=9;++a[1]) // 第一个数的百位 15 for(a[2]=1;a[2]<=9;++a[2]) // 第一个数的十位 16 for(a[3]=1;a[3]<=9;++a[3]) // 第一个数的个位 17 for(a[4]=1;a[4]<=9;++a[4]) // 第二个数的百位 18 for(a[5]=1;a[5]<=9;++a[5]) // 第二个数的十位 19 for(a[6]=1;a[6]<=9;++a[6]) // 第二个数的个位 20 for(a[7]=1;a[7]<=9;++a[7]) // 第三个数的百位 21 for(a[8]=1;a[8]<=9;++a[8]) // 第三个数的十位 22 for(a[9]=1;a[9]<=9;++a[9]) // 第三个数的个位 23 { // 接下来判断每一位上的数互不相等 24 if(a[1]!=a[2] && a[1]!=a[3] && a[1]!=a[4] && a[1]!=a[5] && a[1]!=a[6] && a[1]!=a[7] && a[1]!=a[8] && a[1]!=a[9] 25 && a[2]!=a[3] && a[2]!=a[4] && a[2]!=a[5] && a[2]!=a[6] && a[2]!=a[7] && a[2]!=a[8] && a[2]!=a[9] 26 && a[3]!=a[4] && a[3]!=a[5] && a[3]!=a[6] && a[3]!=a[7] && a[3]!=a[8] && a[3]!=a[9] 27 && a[4]!=a[5] && a[4]!=a[6] && a[4]!=a[7] && a[4]!=a[8] && a[4]!=a[9] 28 && a[5]!=a[6] && a[5]!=a[7] && a[5]!=a[8] && a[5]!=a[9] 29 && a[6]!=a[7] && a[6]!=a[8] && a[6]!=a[9] 30 && a[7]!=a[8] && a[7]!=a[9] && a[8]!=a[9] 31 32 && a[1]*100+a[2]*10+a[3] + a[4]*100+a[5]*10+a[6] == a[7]*100+a[8]*10+a[9] ) 33 { 34 total++; 35 printf("%d%d%d+%d%d%d=%d%d%d ",a[1],a[2],a[3],a[4],a[5],a[6],a[7],a[8],a[9]); 36 } 37 } 38 end = clock(); 39 printf(" total=%d ",total/2); // 因为输出的有重复的 比如 173+286=459 与 286+173=459是一样的 40 printf("total cost time:%lfs ",(end-start)/1000); 41 return 0; 42 }
执行结果部分截图:
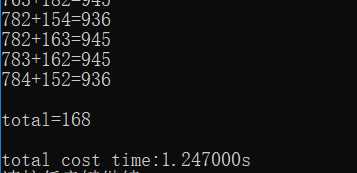
方法二:采用标记(还是枚举法)
1 #include <stdio.h> 2 #include <time.h> 3 4 int main(int argc, char *argv[]) 5 { 6 // 算法改进 用book来标记互不相等的数 7 int a[10],i,total=0,book[10],sum; 8 double start,end; 9 start = clock(); 10 for(a[1]=1;a[1]<=9;++a[1]) // 第一个数的百位 11 for(a[2]=1;a[2]<=9;++a[2]) // 第一个数的十位 12 for(a[3]=1;a[3]<=9;++a[3]) // 第一个数的个位 13 for(a[4]=1;a[4]<=9;++a[4]) // 第二个数的百位 14 for(a[5]=1;a[5]<=9;++a[5]) // 第二个数的十位 15 for(a[6]=1;a[6]<=9;++a[6]) // 第二个数的个位 16 for(a[7]=1;a[7]<=9;++a[7]) // 第三个数的百位 17 for(a[8]=1;a[8]<=9;++a[8]) // 第三个数的十位 18 for(a[9]=1;a[9]<=9;++a[9]) // 第三个数的个位 19 { 20 for(i=1;i<10;++i) // 初始化book数组 21 book[i]=0; 22 for(i=1;i<10;++i) // 如果某个数出现过就标记一下 23 book[a[i]]=1; 24 25 // 统计共出现了多少个不同的数 26 sum = 0; 27 for(i=1;i<10;++i) 28 sum+=book[i]; 29 // 如果正好出现了9个不同的数,并且满足等式条件,则输出 30 if(sum == 9 && a[1]*100+a[2]*10+a[3] + a[4]*100+a[5]*10+a[6] == a[7]*100+a[8]*10+a[9]) 31 { 32 total++; 33 printf("%d%d%d+%d%d%d=%d%d%d ",a[1],a[2],a[3],a[4],a[5],a[6],a[7],a[8],a[9]); 34 } 35 } 36 end = clock(); 37 printf(" total=%d ",total/2); 38 printf("total cost time:%lfs ",(end-start)/1000); 39 return 0; 40 }
执行结果(部分截图):
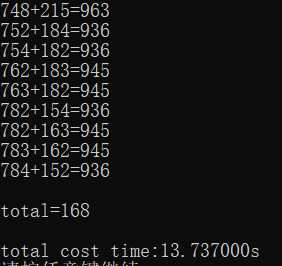
方法三:递归调用
1 #include <stdio.h> 2 #include <time.h> 3 4 int a[10]={0},i,total=0,book[10]={0}; 5 6 void dfs(int step) // step表示现在站在第几个盒子面前 7 { 8 int i; 9 if(step==10) // 如果站在第10个盒子面前,则表示前9个盒子已经放好扑克牌 10 { 11 if(a[1]*100+a[2]*10+a[3] + a[4]*100+a[5]*10+a[6] == a[7]*100+a[8]*10+a[9]) 12 { 13 total++; 14 printf("%d%d%d+%d%d%d=%d%d%d ",a[1],a[2],a[3],a[4],a[5],a[6],a[7],a[8],a[9]); 15 } 16 return; // 返回之前的一步(最近调用的地方) 17 } 18 19 // 此时站在第step个盒子面前,应该放哪张牌呢? 20 // 按照1,2,3,。。。,n的顺序一一尝试 21 for(i=1;i<=9;++i) 22 { 23 // 判断扑克牌i是否还在手上 24 if(book[i]==0) // book[i]为0表示扑克牌还在手上 25 { 26 // 开始尝试使用扑克牌i 27 a[step] = i; // 将扑克牌i放入到第step个盒子中 28 book[i] = 1; 29 30 dfs(step+1); 31 book[i]=0; 32 } 33 } 34 return; 35 } 36 37 int main(int argc, char *argv[]) 38 { 39 double start,end; 40 start = clock(); 41 dfs(1); // 首先站在一个盒子面前 42 end = clock(); 43 printf(" total=%d ",total/2); 44 printf("total cost time:%lfs ",(end-start)/1000); 45 return 0; 46 }
执行结果(部分截图):
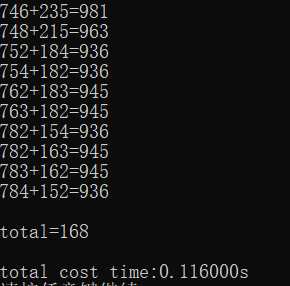
通过比较运行时间,想必大家知道针对统一问题,不同算法效率差别还是挺大的,虽说递归的效率不高,但是在针对小规模数据时,表现还是可以的 。对递归的深入理解可以多看看大咖博客,自己断点跟踪调试。
以上是关于递归之深度优先搜索的主要内容,如果未能解决你的问题,请参考以下文章