线性规划(LP)基本概念和搜索算法

Posted 2023-05-02

参考技术A

可以用一个符号描述一系列类似的数量值

一个方程，如果他是关于决策变量的常熟加权求和形式，则该方程式 线性方程(liner) ，佛则该方程为 非线性方程(non-linear)

目标函数 以及约束方程 中均为关于决策变量的线性方程，则该优化模型为 线性规划(linear program, LP) ，其中目标函数可以为满足约束的任意整数或者分数

目标函数 以及约束方程 中存在关于决策变量的线性方程，则该优化模型为 非线性规划(nonlinear program, LP) ，其中目标函数可以为满足约束的任意整数或者分数

一个优化模型，如果他的决策变量中存在离散变量，则该优化模型位 整数规划(integer program, IP) ，如果整数规划的所有决策变量均为离散变量，则该整数规划为 纯整数规划(pure integer program) ；否则为 混合整数规划(mixed integer program) 。

搜索算法(improving search) 通过检查邻域来寻找比当前更好地解，若有改进则替换当前解，继续迭代，直到邻域中没有更好的解为止。搜索算法又称为 局部改进(local improvement) ， 爬山算法(hillclimbing) ， 局部搜索(local search) 或 邻域搜索(neighborhood search)

倘若一组可行解周围足够小的的邻域内没有优于该解的可行点，则称为 局部最优解(local optimum) ，最小化(最大化)问题存在 局部最小(最大)解 。

如果在全局范围内不存在目标值优于某可行解的其他可行点，则称为 全局最优解(global optimum) ，最小化(最大化)问题存在 全局最小(最大)解

搜索算法沿 由当前点 向下一个搜索点 移动，其中 是当前点 处的 搜索方向(move direction) ， 是沿该方向前进的 步长 ， 。

对于所有足够小的 都有 ,则称 是当前解的一个 改进方向(improving direction) ,如果满足所有约束条件，则为 可行改进方向 。

如果优化模型的目标函数 是光滑的(所有决策变量都是可微的)，那么，当 是一个n维向量的函数，当它有一个一阶片倒数，这些导数组成的n维向量称为 梯度

导数(derivative) ，描述函数随参数的变化率，可以看做斜率。 偏导数(partial derivative) ，是保持其他变量恒定时，关于其中一个变量的导数

对于最大化目标函数 ,若 ，搜索方向 是 处的可改进方向，若 ，搜索方向 不是 处的可改进方向。

对于最小化目标函数 ,若 ，搜索方向 是 处的可改进方向，若 ，搜索方向 不是 处的可改进方向。

当目标函数梯度 ，是最大化目标 的一个改进方向， 是最小化目标函数 的一个改进方向

如果可行域内任意两点的连线都在可行域内，则称该可行域为 凸集 。

离散的可行集总是非凸集

若优化模型的可行集是凸集，那么对任意可行解始终存在指向另一个解的可行方向，意味着，只要存在最优解，可能性不会阻碍局部最优解发展为全局最优解。

线性约束的可行集又称为多面体集。

如果优化模型的所有约束都是线性的，那么该模型的可行域是凸集

两阶段法

大M法

数据结构与算法学习笔记:数据结构基本概念

数据结构与算法基础学习笔记(1):数据结构基本概念

​ 本系列笔记为跟着B站上王卓老师的教程学习所记录的笔记

文章目录

• 数据结构与算法基础学习笔记(1):数据结构基本概念
• • 一.基本概念和术语
  • • 1.数据
    • 2.数据元素
    • 3.数据项
    • 4.数据对象
    • 5.数据结构
    • • 逻辑结构
      • • 划分方法一
        • • （1）线性结构
          • （2）非线性结构
        • 划分方法二:四类基本逻辑结构
        • • (1)集合结构:
          • (2)线性结构:
          • (3)树形结构:
          • (4)图状结构或网状结构:
      • 物理结构(存储结构)
      • • 四种基本的存储结构
        • • 顺序存储结构
          • 链式存储结构
          • 索引存储结构
          • 散列存储结构
      • 逻辑结构与存储结构的关系
    • 6.数据类型和抽象数据类型
    • • ①数据类型
      • ②抽象数据类型
      • • 抽象数据类型的形式定义
        • 抽象数据类型的定义格式
        • • 抽象数据类型(ADT)定义举例：Circle定义
          • 抽象数据类型(ADT)定义举例：复数的定义
  • 二.抽象数据类型的表现与实现
  • • 抽象数据类型如何实现
    • • • • 例:抽象数据类型 "复数" 的实现

一.基本概念和术语

1.数据

• 能输入计算机且被计算机处理的各种符号的集合
• 可分为：
  • 数值型：整数、实数等
  • 非数值型：图片、声音等

2.数据元素

• 是数据的基本单位，在计算机程序中通常作为一个整体进行处理

  如：个人信息表 中 一个人的信息包括 姓名 性别 身高 体重等

• 也称为元素/记录/结点/顶点

3.数据项

• 是构成数据元素的不可分割的最小单位
• 如：上面提到的一个人的信息作为数据元素，其中的姓名、性别、身高、体重分别作为数据项

4.数据对象

• 是性质相同的数据元素的集合，是数据的一个子集

  ​ 数据元素是集合的个体

  ​ 数据对象是集合的子集

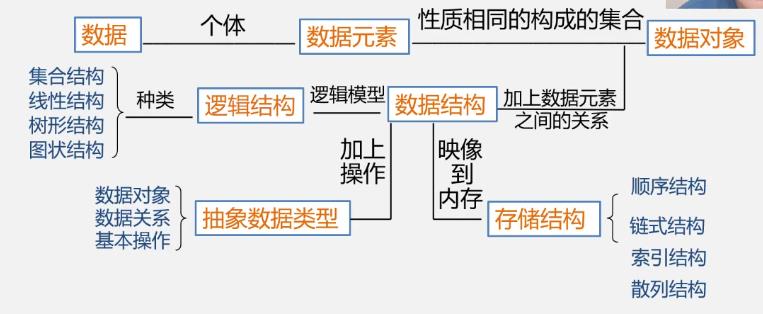
5.数据结构

• 数据元素不是孤立的，数据元素之间的关系称为结构
• 数据结构就是指相互之间存在一种或多种特定关系的数据元素集合
  • 或者说数据结构是带结构的数据元素的集合
• 数据结构包含的内容
  • 逻辑结构：数据元素之间的逻辑关系
  • 物理结构(存储结构)：数据元素及其关系在计算机内存中的表示
  • 数据的运算和实现：对数据元素可以施加的操作以及这些操作在相应的存储结构上的实现

逻辑结构

• 描述数据元素之间的逻辑关系
• 与数据的存储无关，独立于计算机
• 是从具体问题抽象出来的数学模型

划分方法一

（1）线性结构

​ 有且仅有一个开始和一个终端结点，并且所有结点都最多只有一个直接前趋和一个直接后继。

例如:线性表、栈、队列、串

（2）非线性结构

​ 一个结点可能有多个直接前趋和直接后继

例如:树、图

划分方法二:四类基本逻辑结构

(1)集合结构:

结构中的数据元素之间除了同属于一个集合的关系外，无任何其它关系。

(2)线性结构:

结构中的数据元素之间存在着一对一的线性关系。

(3)树形结构:

结构中的数据元素之间存在着一对多的层次关系。

(4)图状结构或网状结构:

结构中的数据元素之间存在着多对多的任意关系。

物理结构(存储结构)

• 数据元素及其关系在计算机存储器中的结构（存储方式)
• 是数据结构在计算机中的表示

四种基本的存储结构

顺序存储结构

• 用一组连续的存储单元依次存储数据元素，数据元素之间的逻辑关系由元素的存储位置来表示。
• C语言中用数组来实现顺序存储结构

链式存储结构

• 用一组任意的存储单元存储数据元素，数据元素之间的逻辑关系用指针来表示。
• 语言中用指针来实现链式存储结构

​ 存储每一个元素本身的同时，还存储了下一个元素的地址

索引存储结构

• 在存储结点信息的同时，还建立附加的索引表
• 索引表中的每一项称为一个索引项
• 索引项的一般形式是:(关键字，地址)
• 关键字是能唯一标识一个结点的那些数据项
• 若每个结点在索引表中都有一个索引项，则该索引表称之为稠密索引(Dense Index)。若一组结点在索引表中只对应一个索引项，则该索引表称之为稀疏索引(Sparse Index)。

​ 如：手机通讯录

散列存储结构

• 根据结点的关键字直接计算出该结点的存储地址

逻辑结构与存储结构的关系

• 存储结构是逻辑关系的映象与元素本身的映象
• 逻辑结构是数据结构的抽象，存储结构是数据结构的实现

6.数据类型和抽象数据类型

​ 引入：

• 在使用高级程序设计语言编写程序时，必须对程序中出现的每个变量、常量或表达式，明确说明它们所属的数据类型。

  • 例如，C语言中:
    • 提供int,char,float, double等基本数据类型
    • 数组、结构、共用体、枚举等构造数据类型
    • 还有指针、空(void)类型
    • 用户也可用typedef自己定义数据类型

• —些最基本数据结构可以用数据类型来实现，如数组、字符串等;

• 而另一些常用的数据结构，如栈、队列、树、图等，不能直接用数据类型来表示。

• 高级语言中的数据类型明显地或隐含地规定了在程序执行期间变量执行期间变量表达的所有可能的取值范围，以及在这些数值范围上所允许进行的操作。

  • 例如，C语言中定义变量i为int类型，就表示i是[-min,max]范围的整数，在这个整数集上可以进行+、-、*、\\、%等操作

①数据类型

​

• 定义：数据类型是一组性质相同的值得集合以及定义于这个值集合上的一组操作的总称

• 数据类型的作用

• 约束变量或常量的取值范围

• 约束变量或常量的操作

• ​ 数据类型=值的集合+值集合上的一组操作

②抽象数据类型

抽象数据类型(ADT)是指一个数学模型以及定义在此数学模型上的一组操作。

• 由用户定义,从问题抽象出数据模型（逻辑结构)
• 还包括定义在数据模型上的一组抽象运算(相关操作)
• 不考虑计算机内的具体存储结构与运算的具体实现算法

抽象数据类型的形式定义

​ 抽象数据类型可用**(D,S,P)**三元组表示

D：数据对象

S:D上的关系集

P:对D的基本操作集

抽象数据类型的定义格式

ADT 抽象数据类型名{
	数据对象:<数据对象的定义>
	数据关系:<数据关系的定义>
	基本操作:<基本操作的定义>
}ADT 抽象数据类型名

其中:

• 数据对象、数据关系的定义用伪代码描述

• 基本操作的定义格式为:

  • 基本操作名（参数表)

  • 初始条件:〈初始条件描述〉

  • 操作结果:〈操作结果描述〉

    基本操作定义格式说明:

    • 参数表:

    赋值参数 只为操作提供输入值
    引用参数以&打头，除可提供输入值外，还将返回操作结果

    • 初始条件:

    描述操作执行之前数据结构和参数应满足的条件，若不满足,则操作失败，并返回相应出错信息。若初始条件为空，则省略之

    • 操作结果：

    说明操作正常完成之后，数据结构的变化状况和应返回的结果

抽象数据类型(ADT)定义举例：Circle定义

ADT 抽象数据类型名{
	Data
	  数据对象的定义
	  数据元素之间逻辑关系的定义
	Operation
	  操作1
	  	初始条件
	  	操作结果描述
	  操作2
	  	......
	  操作n
	  	......
}ADT 抽象数据类型名

ADT Circle{
	数据对象: D={r,x,y|r,x,y均为实数}
	数据关系: R={<r,x,y>|r是半径,<x,y>是圆心坐标}
	基本操作:
	Circle(&C,r,x,y)
			操作结果:构造一个圆
	double Area(C)
			初始条件:圆已存在
			操作结果:计算面积
	double Circumference(C)
			初始条件:圆已存在
			操作结果:计算周长
	......

}ADT Circle

​ Circumference是周长的意思

抽象数据类型(ADT)定义举例：复数的定义

ADT Complex{
	D={r1,r2|r1,r2都是实数}
	S={<r1,r2>|r1是实部,r2是虚部}
	assgin(&C,v1,v2)
		初始条件: 空的复数C已存在
		操作结果: 构造复数C,r1,r2分别被赋以参数v1,v2的值
	destory(&C)
		初始条件:  复数C已存在
		操作结果:  复数C被销毁
	getreal(C,&realPart)
		初始条件:  复数C已存在
		操作结果:  用realPart返回复数C的实部值
	getImag(C,&ImagPart)
		初始条件:  复数C已存在
		操作结果:  用ImagPart返回复数C的虚部值
	add(z1,z2,&sum)
		初始条件: z1,z2是复数
		操作结果: sum返回两个复数z1,z2的和
	......
}ADT Complex

二.抽象数据类型的表现与实现

​ 前面概念小结：

​ 一个问题抽象为一个抽象数据类型后，仅是形式上的抽象定义，还没有达到问题解决的目的，要实现这个目标，就要把抽象的变成具体的，即抽象数据类型在计算机上实现，变为一个能用的具体的数据类型

​ 后续用C语言实现抽象数据类型

• 用已有的数据类型定义描述它的存储结构
• 用函数定义描述它的操作

抽象数据类型如何实现

• 抽象数据类型可以通过固有的数据类型(如整型、实型、字符型导)来表示和实现

  • 即利用处理器中已存在的数据类型来说明新的结构，用已经实现的操作来组合新的操作

    ​ 后续的学习会用类C语言(介于pseudocode(伪代码)和C之间)进行描述

例:抽象数据类型 “复数” 的实现

typedef struct{
	float realpart;		/*实部*/
	float imagpart;		/*虚部*/
}Complex				/*定义复数抽象类型*/
void assign(Complex *A,float real,float imag);	/*赋值*/
void add(Complex *A,float real,float imag);		/*A+B*/
void minus(Complex *A,float real,float imag);	/*A-B*/
void multiply(Complex *A,float real,float imag);	/*A*B*/
void divide(Complex *A,float real,float imag);	/*A/B*/
void assign(Complex *A,float real,float imag){
    A->realpart = real;		/*实部赋值*/
    A->iamgpart = imag;		/*虚部赋值*/
}				/*End of assign()*/
void add(Complex *c,Complex A,Complex B){	
    c->realpart = A.realpart + B.realpart;	/*实部相加*/
    c->imagpart = A.imagpart + B.imagpart;	/*虚部相加*/
}				/*End of add()*/
......

​ 注:

Complex是我们定义的一个结构体类型
带*:指针变量，它是指向Complex类型的指针
不带*:Complex类型的普通变量

如：计算$z=\frac{(8+6i)(4+3i)}{(8+6i)+(4+3i)}$

//类C代码,不纠细节
Complex z1,z2,z3,z4,z;
float RealPart,ImagPart;
assign(z1,8.0,6.0);		//构造复数z1
assign(z2,4.0,3.0);		//构造复数z2
add(z1,z2,z3);			//两个复数相加
multiply(z1,z2,z4);		//两个复数相乘
if(divide(z4,z3,z)){	//两个复数相除
	GetReal(z,RealPart);
	GetImag(z,ImagPart);
}//if

配套B站上王卓老师的教程观看，节约你记笔记的时间❤️❤️❤️