Realtime Rendering 1.1

Posted 2020-11-21 tekkaman

【Realtime Rendering 1.1】

1、A linear transform is one that preserves vector addition and scalar multiplication. Specifically,

　　

 

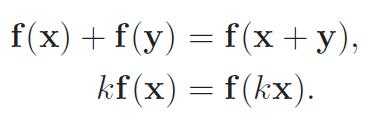
24、Combining linear transforms and translations can be done using an affine transform.

　　An affine transform is one that performs a linear transform and then a translation.

　　The main characteristic of an affine matrix is that it preserves the parallelism of lines, but not necessarily lengths and angles.

　　仿射变换保留了平行性，而没保留长度、角度特性。

25、All rotation matrices have a determinant of one and are orthogonal ,  the determinant of a rotation matrix is always one, since the matrix is orthogonal.

　　旋转不会改变正交矩阵的三个正交基，所以旋转矩阵还是正交矩阵。

　　

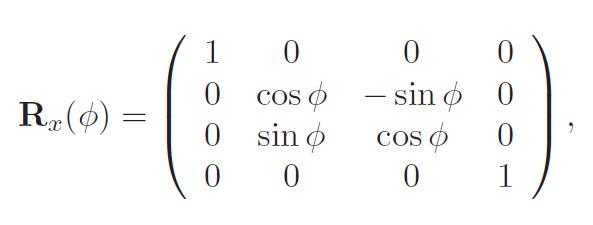
26、This order change can cause incorrect lighting and backface culling to occur. To detect whether a given matrix reflects in some manner, compute the determinant of the upper left 3 × 3 elements of the matrix. If the value is negative, the matrix is reflective.

27、H′ij(s, t) = Hik(s)Hjk(t)。 Finally, it should be noted that since the determinant of any shear matrix |H| = 1, this is a volume preserving transformation.

　　

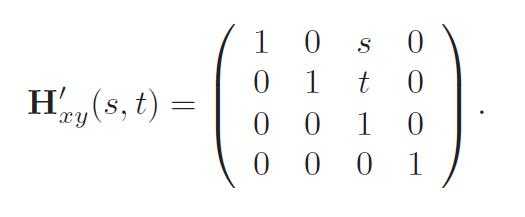
28、a transform, consisting of concatenations of only translations and rotations, is called a rigid-body transform and has the characteristic of preserving lengths, angles, and handedness.

　　

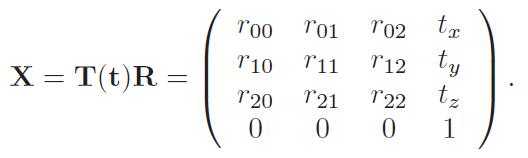
　　The inverse of X is computed as X−1 = (T(t)R)−1 = R−1T(t)−1 = RTT(−t).

 

29、the proper method transform normal is to use the transpose of the matrix’s adjoint.  The traditional answer for transforming the normal is that the transpose of the inverse is computed [1277]. This method normally works. The full inverse is not necessary, however, and occasionally cannot be created. The inverse is the adjoint divided by the original matrix’s determinant. If this determinant is zero, the matrix is singular, and the inverse does not exist.

　　　　

30、旋转矩阵

　　

　　

　　

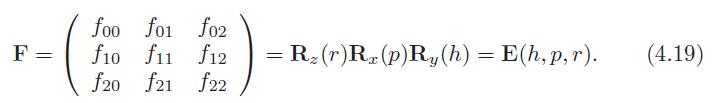
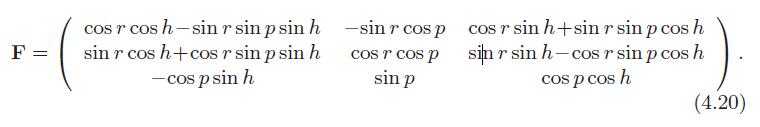
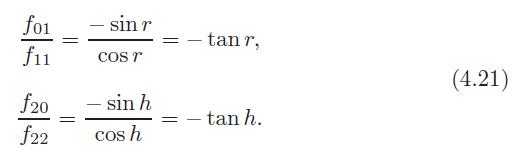
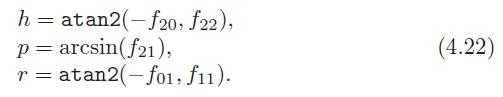
31、We have already presented two decompositions, those of deriving the translation and rotation matrix for a rigid-body transformation (see Section 4.1.6) and deriving the Euler angles from an orthogonal matrix (Section 4.2.2).

　　It is trivial to retrieve the translation matrix, as we simply need the elements in the last column of the 4×4 matrix.

　　We can also determine if a reflection has occurred by checking whether the determinant of the matrix is negative.

32、绕任意轴旋转。

　　

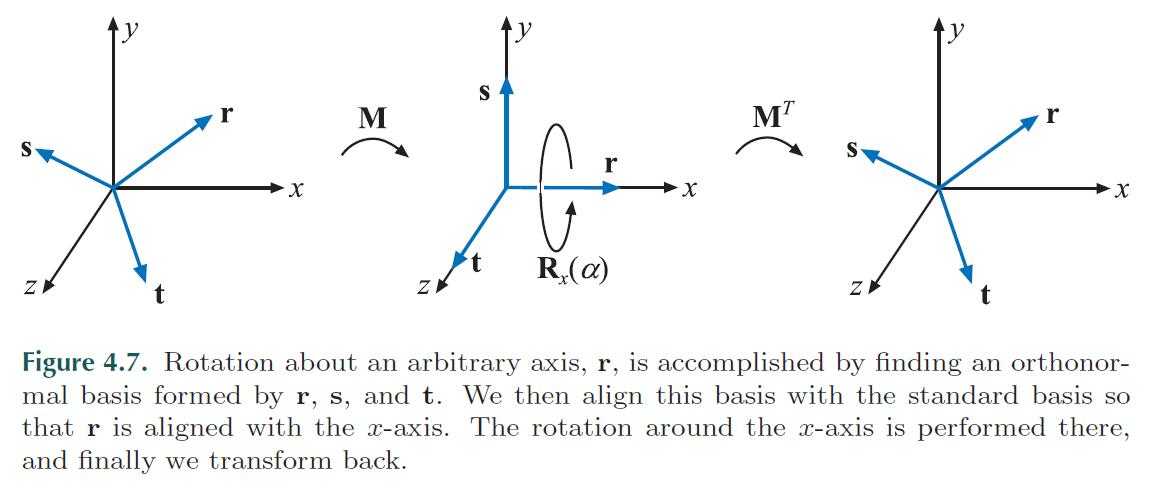
33、根据给定r，计算出basis：r,s,t。

　　find the smallest component (in absolute value) of r, and set it to 0. Swap the two remaining components, and then negate the first9 of these.

　　

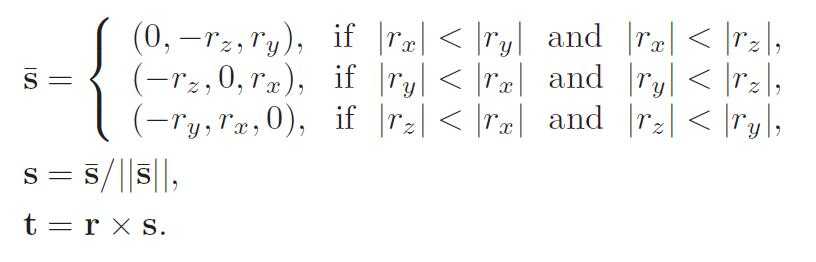
　　This matrix transforms the vector r into the x-axis (ex), s into the y-axis, and t into the z-axis.  the final transform for rotating α radians around the normalized vector r is then.

　　

　　

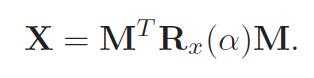
　　Goldman公式：

　　

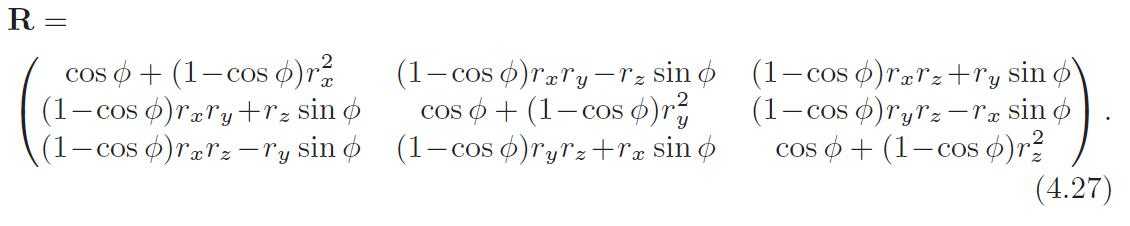
34、 For every 3 × 3 rotation matrix,1 R, that rotates φ radians around any axis, the trace (see page 898 for a definition) is constant independent of the axis.

　　

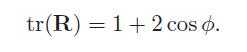
35、四元数的逆。

共轭复数有些有趣的性质:

　　

　　

 

　　

　　

　　

　　

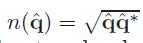
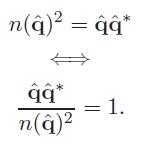
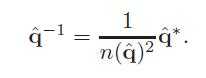
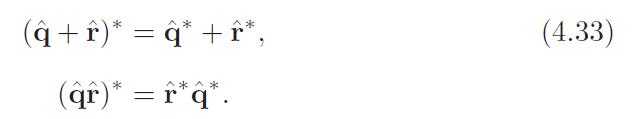
36、单位四元数可以写成下面这样。

　　

　　

　　

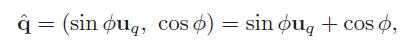
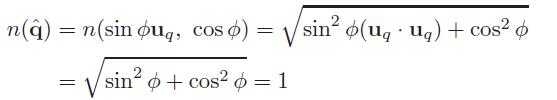
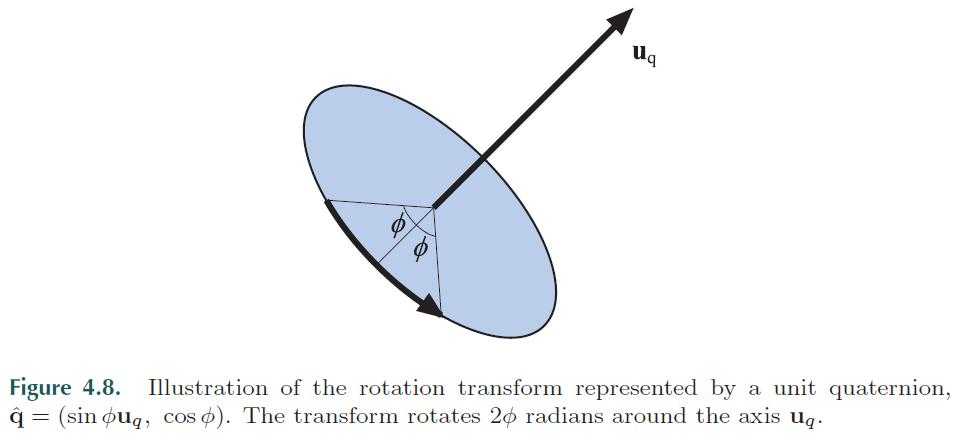
37、put the four coordinates of a point or vector p = (px py pz pw)T into the components of a quaternion ˆp, and assume that we have a unit quaternion ˆq = (sinφuq, cos φ).

　　

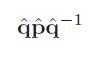
　　rotates ˆp (and thus the point p) around the axis uq by an angle 2φ. Note that since ˆq is a unit quaternion, ˆq−1 = ˆq∗. This rotation, which clearly can be used to rotate around any axis

 

　　Given two unit quaternions, ˆq and ˆr, the concatenation of first applying ˆq and then ˆr to a quaternion, ˆp (which can be interpreted as a point p), is given by Equation 4.41:

　　

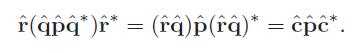
38、A quaternion, ˆq, can be converted into a matrix Mq.

　　

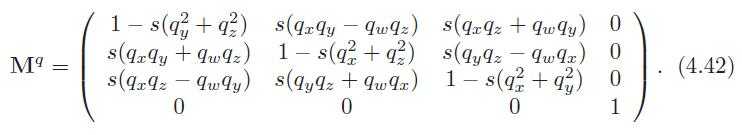
　　Here, the scalar is s = 2/n(ˆq). For unit quaternions, this simplifies to:

　　

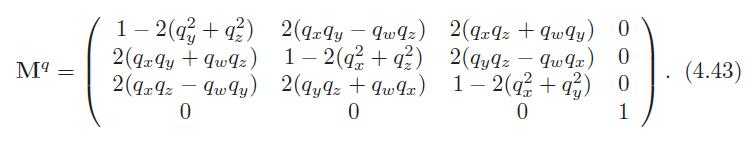
　　由 4.44 + 4.45 可以从M推导出四元数4.46：

　　

　　

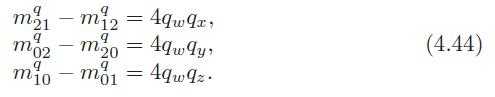
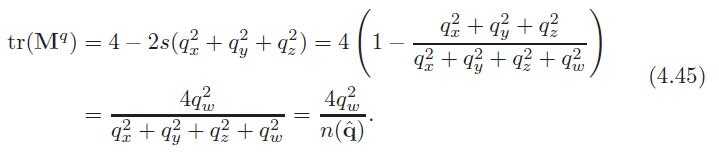
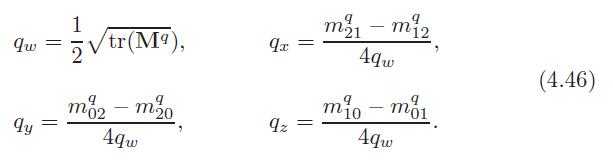
　　令  t = q2w −q2x −q2y −q2，可以得到避免除法的公式：

　　

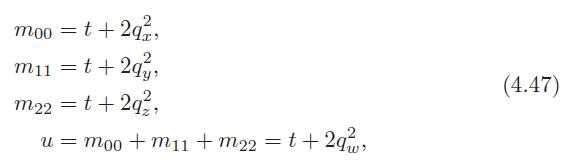
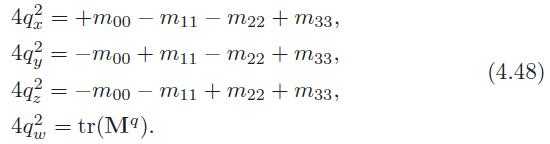
39、The algebraic form of Spherical linear interpolation:

　　

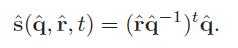
　　However, for software implementations, the following form, where slerp stands for spherical linear interpolation, is much more appropriate:

　　

　　

　　

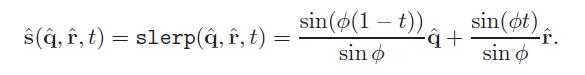
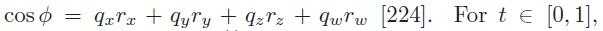
　　The slerp function is perfectly suited for interpolating between two orientations and it behaves well (fixed axis, constant speed). This is not the case with when interpolating using several Euler angles.

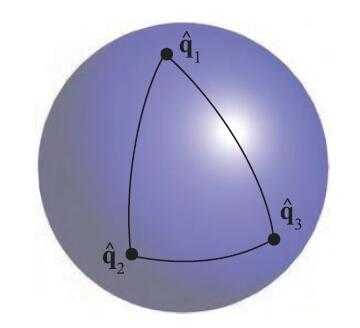
40、 球面样条插值。Squad。 

　　introduce quaternions ˆai and ˆai+1 between ˆqi and ˆqi+1.

　　

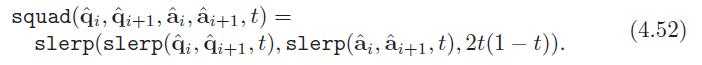
41、After some algebraic and trigonometric simplification of Equation 4.43,the rotation matrix becomes [893]:

　　

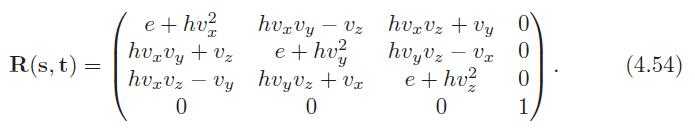
　　In this equation, we have used the following intermediate calculations:

　　

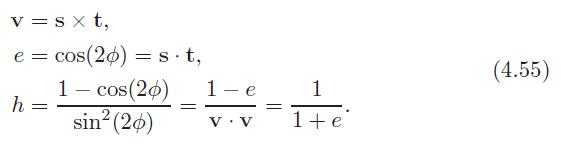
　　 As can be seen, all square roots and trigonometric functions have disappeared due to the simplifications, and so this is an efficient way to create the matrix.

42、Vertex Blending

　　the entire mesh is often called a skin.

　　p is the original vertex, and u(t) is the transformed vertex whose position depends on the time t. There are n bones influencing the position of p, which is expressed in world coordinates.  The matrix Mi transforms from the initial bone’s coordinate system to world coordinates. Typically a bone has its controlling joint at the origin of its coordinate system. The Bi(t) matrix is the ith bone’s world transform that changes with time to animate the object,

　　

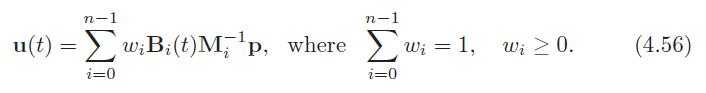
　　the final location is interpolated from the set of computed points. The matrix Mi is not explicitly shown in some discussions of skinning, but rather is considered as being a part of Bi(t).

　　the transformed point u will lie in the convex hull of the set of points Bi(t)M−1 i p, for all i = 0. . .n − 1 (fixed t).

43、Morphin(Vertex Morphing)：混合顶点

　　Morph targets：基Model + Diff。如下图：

　　

　　

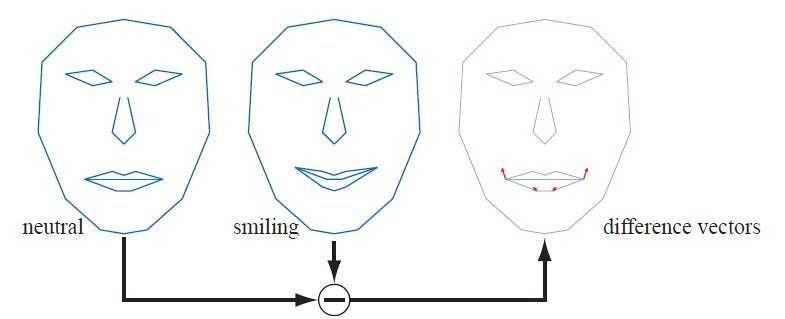
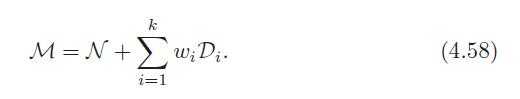
　　Skinning、Morph Target 一起使用可以达到非常好的效果。

　　

　　

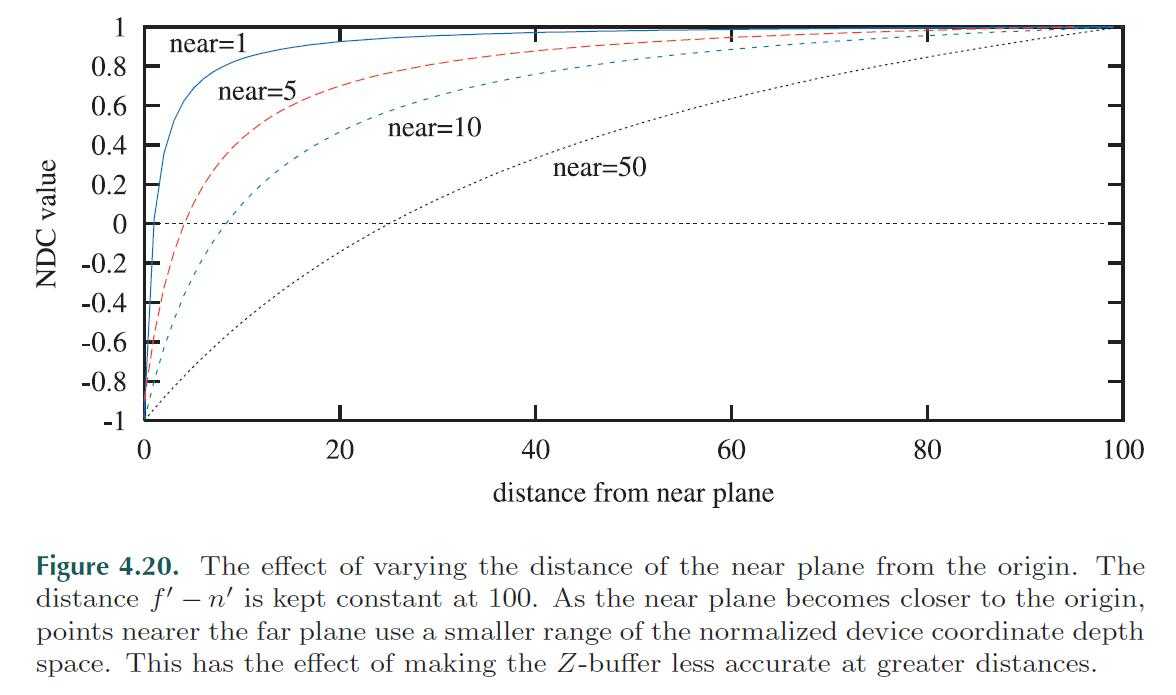
44、透视投影中 z 值是非线性的。

　　One effect of using a perspective transformation is that the computed depth value does not vary linearly with the input pz value. For example, if n′ = 10 and f′ = 110 (using the OpenGL terminology), when pz is 60 units down the negative z-axis (i.e., the halfway point) the normalized device coordinate depth value is 0.833, not 0.