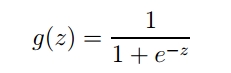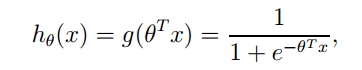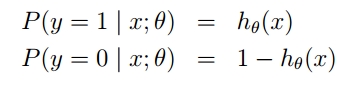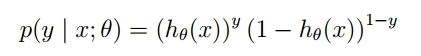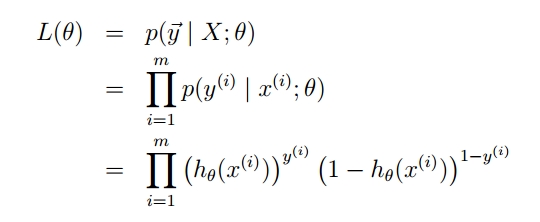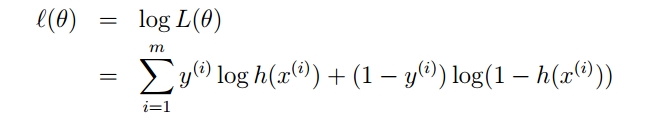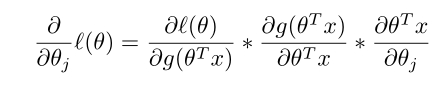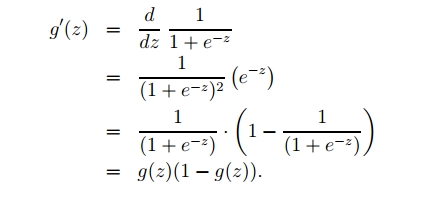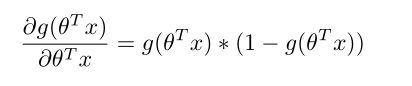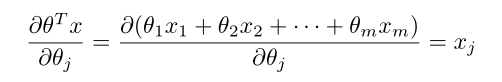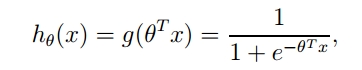Logistic本质上是一个基于条件概率的判别模型(DiscriminativeModel)。
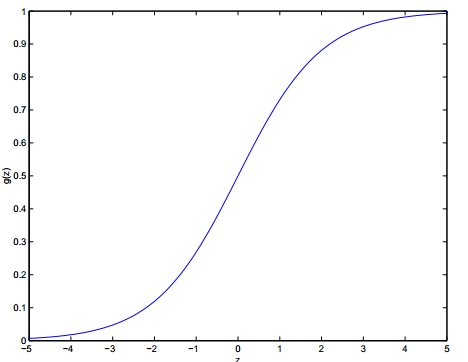
函数图像为:
通过sigma函数计算出最终结果,以0.5为分界线,最终结果大于0.5则属于正类(类别值为1),反之属于负类(类别值为0)。
如果将上面的函数扩展到多维空间,并且加上参数,则函数变成:
接下来问题来了,如何得到合适的参数向量θ呢?
由于sigma函数的特性,我们可作出如下的假设:
上式即为在已知样本X和参数θ的情况下,样本X属性正类(y=1)和负类(y=0)的条件概率。
将两个公式合并成一个,如下:
既然概率出来了,那么最大似然估计也该出场了。假定样本与样本之间相互独立,那么整个样本集生成的概率即为所有样本生成概率的乘积:
为了简化问题,我们对整个表达式求对数,(将指数问题对数化是处理数学问题常见的方法):
满足似然函数(θ)的最大的θ值即是我们需要求解的模型。
梯度上升算法
就像爬坡一样,一点一点逼近极值。爬坡这个动作用数学公式表达即为:
其中,α为步长。
回到Logistic Regression问题,我们同样对函数求偏导。
先看:
其中:
再由:
可得:
接下来就剩下第三部分:
(这个公式应该很容易理解,简单的偏导公式)
还有就是:
综合三部分即得到:
因此,梯度迭代公式为:
结合本式再去理解《机器学习实战》Page 78中的代码就很简单了。