用孩子兄弟链表表示的树，查找其某一个数据等于a的节点

Posted 2023-04-30

我写了一个用孩子兄弟链表法表示的树，想查找这棵树中数据等于a的节点，有哪位高人可以帮我写一个C版或者Java版的，或者伪代码也可以~谢谢啦~~

参考技术A #ifndef BinaryTree_H
#define BinaryTree_H

＃i nclude <stdlib.h>
＃i nclude <stack>

class BinaryTree

private:
typedef int Item;
typedef struct TreeNode

Item Node;
TreeNode* pRight;
TreeNode* pLeft;

TreeNode(Item node = 0, TreeNode* pright = NULL, TreeNode* pleft = NULL)
: Node(node)
, pRight(pright)
, pLeft(pleft)



TreeNode, *PTreeNode;

public:
enum TraverseType

PREORDER = 0, // 前序
INORDER = 1, // 中序
POSTORDER = 2, // 后序
LEVELORDER = 3 // 层序
;

BinaryTree(Item Array[], int nLength);
~BinaryTree();

PTreeNode GetRoot()

return m_pRoot;


// 遍历树的对外接口
// 指定遍历类型和是否是非递归遍历,默认是递归遍历
void Traverse(TraverseType traversetype, bool bRec = true);

private:
PTreeNode CreateTreeImpl(Item Array[], int nLength);
void DetroyTreeImpl(PTreeNode pTreenode);

void PreTraverseImpl(PTreeNode pTreenode); // 递归前序遍历树
void InTraverseImpl(PTreeNode pTreenode); // 递归中序遍历树
void PostTraverseImpl(PTreeNode pTreenode); // 递归后序遍历树

void NoRecPreTraverseImpl(PTreeNode pTreenode); // 非递归前序遍历树
void NoRecInTraverseImpl(PTreeNode pTreenode); // 非递归中序遍历树
void NoRecPostTraverseImpl(PTreeNode pTreenode); // 非递归后序遍历树

void LevelTraverseImpl(PTreeNode pTreenode);

PTreeNode m_pRoot; // 根结点

// 采用STL里面的stack作为模拟保存链表结点的stack容器
typedef std::stack<BinaryTree::PTreeNode> TreeNodeStack;
;

#endif

BinaryTree.cpp:

/********************************************************************
created: 2006/07/04
filename: BinaryTree.cpp
author: 李创

purpose: 演示二叉树的算法
*********************************************************************/

＃i nclude <iostream>
＃i nclude <assert.h>
＃i nclude <queue>
＃i nclude "BinaryTree.h"

BinaryTree::BinaryTree(Item Array[], int nLength)
: m_pRoot(NULL)

assert(NULL != Array);
assert(nLength > 0);

m_pRoot = CreateTreeImpl(Array, nLength);


BinaryTree::~BinaryTree()

DetroyTreeImpl(m_pRoot);


// 按照中序递归创建树
BinaryTree::PTreeNode BinaryTree::CreateTreeImpl(Item Array[], int nLength)

int mid = nLength / 2;
PTreeNode p = new TreeNode(Array[mid]);

if (nLength > 1)

p->pLeft = CreateTreeImpl(Array, nLength / 2);
p->pRight = CreateTreeImpl(Array + mid + 1, nLength / 2 - 1);


return p;


void BinaryTree::DetroyTreeImpl(PTreeNode pTreenode)

if (NULL != pTreenode->pLeft)

DetroyTreeImpl(pTreenode->pLeft);

if (NULL != pTreenode->pRight)

DetroyTreeImpl(pTreenode->pRight);


delete pTreenode;
pTreenode = NULL;


// 遍历树的对外接口
// 指定遍历类型和是否是非递归遍历,默认是递归遍历
void BinaryTree::Traverse(TraverseType traversetype, bool bRec /*= true*/)

switch (traversetype)

case PREORDER: // 前序

if (true == bRec)

std::cout << "递归前序遍历树\n";
PreTraverseImpl(m_pRoot);

else

std::cout << "非递归前序遍历树\n";
NoRecPreTraverseImpl(m_pRoot);


break;

case INORDER: // 中序

if (true == bRec)

std::cout << "递归中序遍历树\n";
InTraverseImpl(m_pRoot);

else

std::cout << "非递归中序遍历树\n";
NoRecInTraverseImpl(m_pRoot);


break;

case POSTORDER: // 后序

if (true == bRec)

std::cout << "递归后序遍历树\n";
PostTraverseImpl(m_pRoot);

else

std::cout << "非递归后序遍历树\n";
NoRecPostTraverseImpl(m_pRoot);


break;

case LEVELORDER: // 层序

std::cout << "层序遍历树\n";
LevelTraverseImpl(m_pRoot);



std::cout << std::endl;


// 递归前序遍历树
void BinaryTree::PreTraverseImpl(PTreeNode pTreenode)

if (NULL == pTreenode)
return;

std::cout << "Item = " << pTreenode->Node << std::endl;

PreTraverseImpl(pTreenode->pLeft);

PreTraverseImpl(pTreenode->pRight);


// 非递归前序遍历树
void BinaryTree::NoRecPreTraverseImpl(PTreeNode pTreenode)

if (NULL == pTreenode)
return;

TreeNodeStack NodeStack;
PTreeNode pNode;
NodeStack.push(pTreenode);

while (!NodeStack.empty())

while (NULL != (pNode = NodeStack.top())) // 向左走到尽头

std::cout << "Item = " << pNode->Node << std::endl; // 访问当前结点
NodeStack.push(pNode->pLeft); // 左子树根结点入栈

NodeStack.pop(); // 左子树根结点退

栈
if (!NodeStack.empty())

pNode = NodeStack.top();
NodeStack.pop(); // 当前结点退栈
NodeStack.push(pNode->pRight); // 当前结点的右子树根结点入栈




// 中序遍历树
// 中序遍历输出的结果应该和用来初始化树的数组的排列顺序一致
void BinaryTree::InTraverseImpl(PTreeNode pTreenode)

if (NULL == pTreenode)
return;

if (NULL != pTreenode->pLeft)

InTraverseImpl(pTreenode->pLeft);


std::cout << "Item = " << pTreenode->Node << std::endl;

if (NULL != pTreenode->pRight)

InTraverseImpl(pTreenode->pRight);



// 非递归中序遍历树
void BinaryTree::NoRecInTraverseImpl(PTreeNode pTreenode)

if (NULL == pTreenode)
return;

TreeNodeStack NodeStack;
PTreeNode pNode;
NodeStack.push(pTreenode);

while (!NodeStack.empty())

while (NULL != (pNode = NodeStack.top())) // 向左走到尽头

NodeStack.push(pNode->pLeft);


NodeStack.pop();

if (!NodeStack.empty() && NULL != (pNode = NodeStack.top()))

std::cout << "Item = " << pNode->Node << std::endl;
NodeStack.pop();
NodeStack.push(pNode->pRight);




// 后序遍历树
void BinaryTree::PostTraverseImpl(PTreeNode pTreenode)

if (NULL == pTreenode)
return;

if (NULL != pTreenode->pLeft)

PostTraverseImpl(pTreenode->pLeft);


if (NULL != pTreenode->pRight)

PostTraverseImpl(pTreenode->pRight);


std::cout << "Item = " << pTreenode->Node << std::endl;


// 非递归后序遍历树
void BinaryTree::NoRecPostTraverseImpl(PTreeNode pTreenode)

if (NULL == pTreenode)
return;

TreeNodeStack NodeStack;
PTreeNode pNode1, pNode2;
NodeStack.push(pTreenode);
pNode1 = pTreenode->pLeft;

bool bVisitRoot = false; // 标志位,是否访问过根结点
while (!NodeStack.empty())

while (NULL != pNode1) // 向左走到尽头

NodeStack.push(pNode1);
pNode1 = pNode1->pLeft;


pNode1 = NodeStack.top();
NodeStack.pop();

if (NULL == pNode1->pRight) // 如果没有右子树就是叶子结点

std::cout << "Item = " << pNode1->Node << std::endl;
pNode2 = pNode1;
pNode1 = NodeStack.top();

if (pNode2 == pNode1->pRight) // 如果这个叶子结点是右子树

std::cout << "Item = " << pNode1->Node << std::endl;
NodeStack.pop();
pNode1 = NULL;

else // 否则访问右子树

pNode1 = pNode1->pRight;


else // 访问右子树

if (pNode1 == pTreenode && true == bVisitRoot) // 如果已经访问过右子树那么就退出

std::cout << "Item = " << pNode1->Node << std::endl;
return;

else

if (pNode1 == pTreenode)

bVisitRoot = true;


NodeStack.push(pNode1);
pNode1 = pNode1->pRight;





// 按照树的层次从左到右访问树的结点
void BinaryTree::LevelTraverseImpl(PTreeNode pTreenode)

if (NULL == pTreenode)
return;

// 层序遍历用于保存结点的容器是队列
std::queue<PTreeNode> NodeQueue;
PTreeNode pNode;
NodeQueue.push(pTreenode);

while (!NodeQueue.empty())

pNode = NodeQueue.front();
NodeQueue.pop();
std::cout << "Item = " << pNode->Node << std::endl;

if (NULL != pNode->pLeft)

NodeQueue.push(pNode->pLeft);

if (NULL != pNode->pRight)

NodeQueue.push(pNode->pRight);




main.cpp

/********************************************************************
created: 2006/07/04
filename: main.cpp
author: 李创

purpose: 测试二叉树的算法
*********************************************************************/

＃i nclude "BinaryTree.h"

＃i nclude <stdio.h>
＃i nclude <stdlib.h>
＃i nclude <time.h>
＃i nclude <iostream>

void DisplayArray(int array[], int length)

int i;

for (i = 0; i < length; i++)

printf("array[%d] = %d\n", i, array[i]);



void CreateNewArray(int array[], int length)

for (int i = 0; i < length; i++)

array[i] = rand() % 256 + i;



int main()

int array[10];
srand(time(NULL));

// 创建数组
CreateNewArray(array, 10);
DisplayArray(array, 10);

BinaryTree *pTree = new BinaryTree(array, 10);

// 测试前序遍历
pTree->Traverse(BinaryTree::PREORDER);
std::cout << "root = " << pTree->GetRoot()->Node << std::endl;
std::cout << "root->left = " << pTree->GetRoot()->pLeft->Node << std::endl;
std::cout << "root->right = " << pTree->GetRoot()->pRight->Node << std::endl;
pTree->Traverse(BinaryTree::PREORDER, false);

// 测试中序遍历
pTree->Traverse(BinaryTree::INORDER);
std::cout << "root = " << pTree->GetRoot()->Node << std::endl;
std::cout << "root->left = " << pTree->GetRoot()->pLeft->Node << std::endl;
std::cout << "root->right = " << pTree->GetRoot()->pRight->Node << std::endl;
pTree->Traverse(BinaryTree::INORDER, false);
// 测试后序遍历
pTree->Traverse(BinaryTree::POSTORDER);
std::cout << "root = " << pTree->GetRoot()->Node << std::endl;
std::cout << "root->left = " << pTree->GetRoot()->pLeft->Node << std::endl;
std::cout << "root->right = " << pTree->GetRoot()->pRight->Node << std::endl;
pTree->Traverse(BinaryTree::POSTORDER, false);
// 测试层序遍历
pTree->Traverse(BinaryTree::LEVELORDER);

system("pause");

delete pTree;

return 0;

整合！！

树的孩子兄弟表示法建树

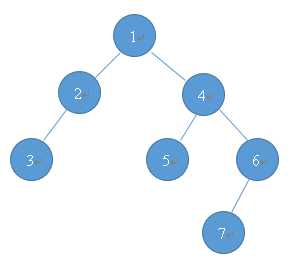
　　树的表示方法有很多，在董永建老师的一本通里也有介绍，其中一种表示方法为孩子兄弟表示 法，但董老师没给出例程，经本人琢磨，勉强写了一个。

　　如右图所示一棵，树的建立基本仿照扩展二叉树的原理，建树时，首先输入根值，接着再输入其所有孩子的值，以0结束。（若输入某个节点的所有孩子时，直接输入0，则说明这是一个叶节点，没有孩子）。

　　根据这一规则，右图所示的树可依次输入1 2 4 0 3 0 0 5 6 0 0 7 0 0。为了检查是否建树成功，顺便写了个先根遍历输出，结果为：1-2-3-4-5-6-7。实现原理：单链表结构。

#include<iostream>
using namespace std;
typedef struct node;
typedef node * tree;
struct node{//孩子兄弟表示法 
    int n;
    tree ch,next;//分别存放第一个孩子，并用链表结构存其兄弟 
};
void creat(tree &p)
{
    cout<<p->n<<‘:‘;//输出根值，方便输入,其后依次输入各个孩子，以0结束 
    int x;
    //开始输入第一个孩子 
    cin>>x;
    if(x)
    {
        p->ch=new node;
        p->ch->n=x,p->ch->next=NULL,p->ch->ch=NULL;
    }
    else
    {
        p->ch=NULL; 
         return;//第一个孩子不存在，就不会有第二个孩子，也不会有孙子 
    }
    //输入第一个孩子的兄弟 
    tree t=p->ch;
    cin>>x;
    while(x)
    {
        t->next=new node;
        t->next->n=x;
        t=t->next;
        t->ch=NULL,t->next=NULL;
        cin>>x;
    }
    //递归每一个孩子的子树 
    t=p->ch;
    while(t)
     {
         creat(t);
         t=t->next;
     }
}
void pr(tree p)//前序输出这棵树 
{
    tree t=p->ch;
    while(t)
    {
        cout<<‘-‘<<t->n;
        pr(t);
        t=t->next;
    }
}
int main(){
    tree p=new node,h;
    h=p;
    cin>>p->n;
    creat(p);
    cout<<p->n;
    pr(p);
    return 0;
}

全树程序

 　　如果树是二叉树，当然程序应该可以更简单一些。（每次都输入左、右儿子的值，如果相应儿子没就输入0，最后不用补0）。样例输入1 2 4 3 0 0 0 5 6 0 0 7 0 0 0。样例输出：1 2 3 4 5 6 7。

#include<iostream>
using namespace std;
typedef struct node;
typedef node *tree;
struct node{
    int num;
    tree l,r;
}; 
void bult(tree &p)//引用形参，确保数据同步更改 
{
    int x,y;
    cout<<p->num<<‘:‘;
    cin>>x>>y;
    if(x)
    {
        p->l=new node;
        p->l->num=x;
        bult(p->l);
    }
    else p->l=NULL;
    if(y)
    {
        p->r=new node;
        p->r->num=y;
        bult(p->r);
    }
    else p->r=NULL;
}
void pr(node *p)
{
    if(p)
    {
        cout<<p->num<<‘ ‘;
        pr(p->l);
        pr(p->r);
    }
}
int main(){
    node *h,*p=new node;
    h=p;
    cin>>p->num;
    bult(p);
    pr(h);
    return 0;
}

二叉树程序

 

　　如有写的不妥，请大神指教，不胜感激！