Riesz表示定理和Lax-Milgram定理

Posted 2023-04-30

参考技术A

本文中设 是一个 ( 或 )上的Hilbert空间.
命题1. 设 是 中的一个闭凸集, , 则存在唯一的 使得 .
证明. 我们先证存在性. 记 , 设 使得 , 我们想证 收敛到某个 . 为此我们对 写出平行四边形等式:

由此可知


故 是Cauchy列, 而 完备, 闭, 故存在 使得 , 由范数的连续性即知 .
我们再证唯一性. 如果 使得 , 那么我们对 使用平行四边形等式得到


从而 , 这就证明了唯一性.

下面我们设 是 的闭子空间.
命题2. .
证明. 我们先证明 . 任取 , 如果 , 当然有 , 如果 , 那么存在 使得 , 现在我们想证 . 为此我们任取 , 想证 . 考虑二次函数 , 由 的定义知 在 处取到最小值, 故 . 以 替换 可得 . 从而 .
这说明 , 即 , .
我们再证 . 若 有两个分解 , 其中 , 则 , 从而 . 这说明这两个分解是一样的, 故 .

定义1. 设 , 定义 为 在 上的最佳逼近元.
注记. 由我们之前的讨论可以知道 .

命题3. 对任何 , 有 .
证明. 首先由之前的讨论我们有 , 这里 . 如果我们能证明 , 那么由这种分解的唯一性即可推知结论.
显然 , 为了证明另一边, 我们任取 . 我们有分解 , 而 , 故 , 从而 . 这样就证明了 .

我们现在对线性泛函的一般性质做一个小讨论.

定义2. 设 是某个域 上的线性空间, 是它的子空间, 的余维数被定义为 .
命题4. 设 是某个域 上的线性空间, 是 上的线性函数, 则 的子空间 的余维数为1.
证明. 因 , 故 . 现在任取非零元素 , 则 . 此时我们有 , 从而

即 线性相关, 故 . 故 .

现在我们回到Hilbert空间的讨论. 我们之前证明了 , 此时我们还有线性同构 . 故 的余维数就是 的维数. 若 是 上的连续线性泛函, 那么 .

定理1(Riesz表示定理). 设 , 则存在唯一的 使得 , .
证明. 先证存在性. 若 , 则取 即可. 当 时, . 我们任取 , 再令 . 我们想说明这就是我们要寻找的 .
任取 , 设 , 则


接着我们再证唯一性. 如果 都满足要求, 那么对任何 , 我们有 , 取 即知 , 即 .

定理2(实的Lax-Milgram定理). 设 是 上的Hilbert空间, 是 上的双线性形式, 并且存在 使得 , , , 则对任何 , 存在唯一的 使得 , .
证明. 对任何 , 我们定义线性泛函 , 则显然 , 故 连续. 由Riesz表示定理, 存在 使得 , 这样我们就定义了一个线性映射 . 如果我们能说明 是满的, 那么由Riesz表示定理, 存在 使得 , 再由 满可设 , 则 .
现在我们集中精力证明 满.
首先,由于 , 故 , 从而 连续. 另一方面, , 从而 , 故 单.
我们再说明 的值域 是闭的. 设 , 则 是Cauchy列, 由 知 也是Cauchy列, 故可设 . 由 连续性知 , 故 . 从而 , 闭.
现在由于 , 故我们只需证明 即可. 任取 , 有 , 从而 . 这就说明了 是满的, 从而定理得证.

函数

函数的基本概念

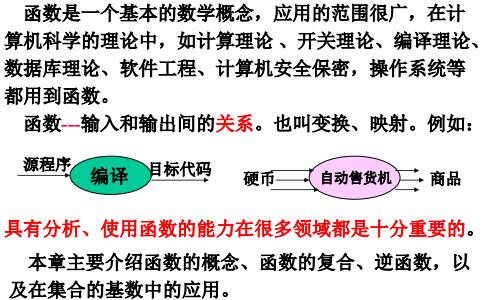
概念

定义

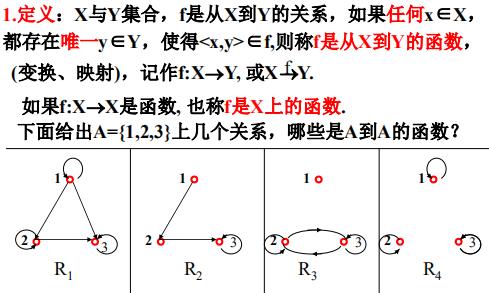
自变元与函数值(像源与映像)

定义域、值域和陪域(共域)

函数的表示方法

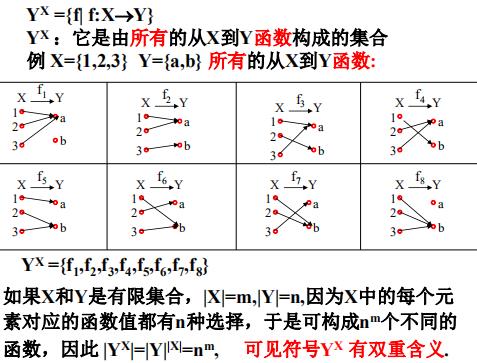
从X到Y函数的集合Yˣ

特殊函数

常值函数

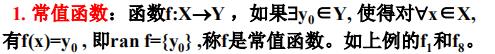
恒等函数

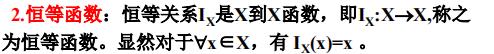
两个函数相等

函数的类型

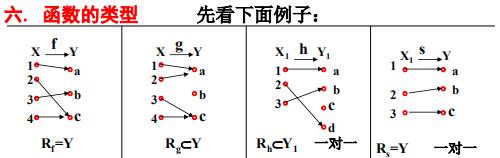
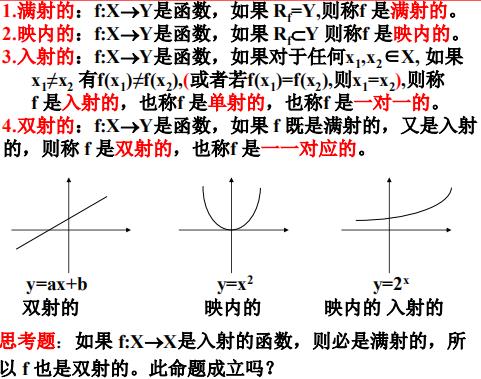
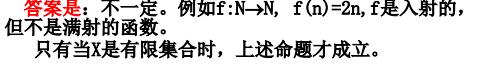
小结

函数的复合

定义

复合函数的计算

函数复合的性质

定理5-2.1

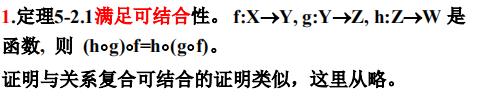
定理5-2.2

定理5-2.3

定理5-2.4

逆函数

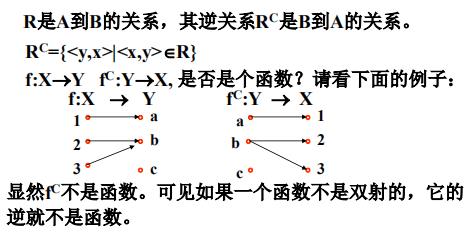
定义

性质

定理5-3.1

定理5-3.2

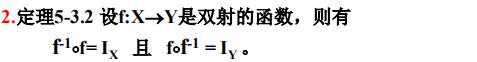
定理5-3.3

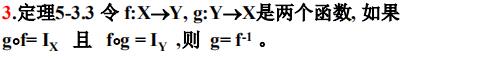
定理5-3.4

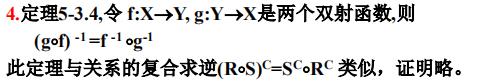
集合的特征函数与模糊子集

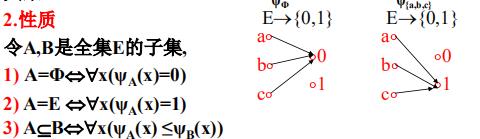
集合的特征函数

定义

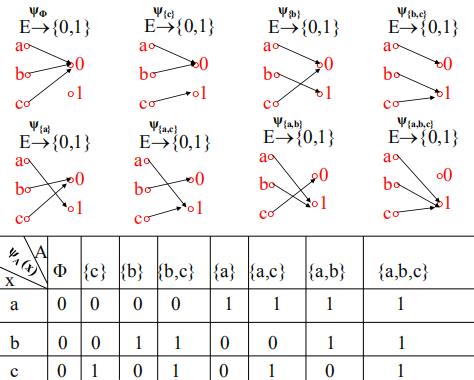
性质

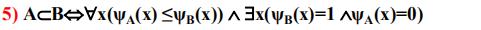
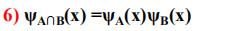
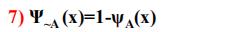
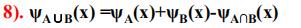
模糊子集

定义

模糊子集的表示方法

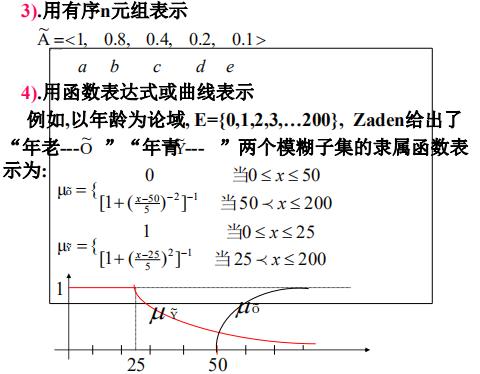
模糊集合的运算

集合的基数

自然数

集合A的后继集合A+

自然数集合N的定义(Peano公理)

集合的等势

定义

集合间的等势关系“~”是个等价关系

基数类和基数

基数类

基数

有限集合与无限集合

可数集合及其基数

自然数集合N的基数

可数集

可数集的判定

定理5-5.1

至多可数集

不可数集合及其基数

实数轴上的(0,1)区间中的实数是不可数的

连续统基数

计算公式

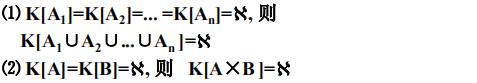
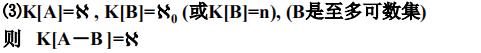
基数的比较

定理5-5.2

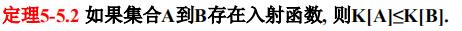
定理5-5.3(Zermelo定理)

定理5-5.4(Contor- Schroder- Bernstein定理)

定理5-5.5

定理5-5.6

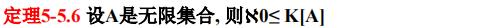
连续统假设

小结

小结