ansys下面的变形的单位是啥啊

Posted 2023-04-25

如图下面从蓝色到红色， .297124 至2.243表明的是什么啊 是变形的百分比还是2.243mm

变形的单位是长度尺寸，但具体是mm、cm还是m则取决于你建立模型时使用的单位。 参考技术A 带单位的... 参考技术B 不是百分比。是变形的数值。 参考技术C 看你查看的是后处理里哪一项追问

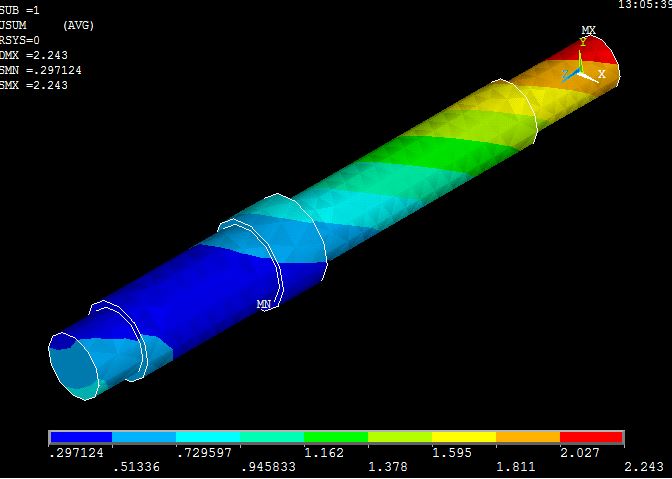
这个是变形的

追答

你查看的是位移矢量和，这个的单位和你建模时模型的单位与加载载荷时的单位有关。
举个例子。
比如是一块长宽高分别为1米、1米、1米的铁块，施加10000000Pa的载荷 ，看变形结果。
你在建模时就是用的1、1、1和10000000建的（建模时后面不加单位的，单位在你自己脑子里），最后后处理的数值后面的单位就是米和牛顿这些单位算出来的量纲：米

如果你建模时模型的单位是1000（你脑海里默认的模型单位是毫米），载荷还是用10000000。这时后处理出来的数值就是以毫米为单位的。

懂了没。

追问

大侠，我能再问一个问题吗，我要是求固有频率那的单位那如果还是这个1mX1mX1m的铁块，我建摸用心中默认米做的单位也就是到的频率如下，这个是不是HZ的意思啊。但我要用毫米作单位那，得到的频率TIME/DREQ是下面的数字除以1000，但单位单位是Khz，是吧。

追答

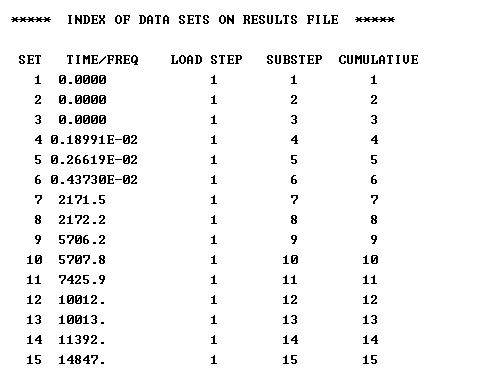
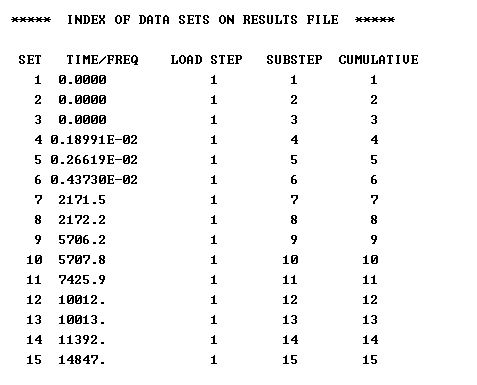
算固有频率的时候只改模型参数的话，数值会出现非线性变化。因为材料的弹性模量的量纲都得改，不然就不是差1000倍了。

本回答被提问者采纳

欧几里德算法是啥啊?

欧几里德算法
欧几里德算法又称辗转相除法，用于计算两个整数a,b的最大公约数。其计算原理依赖于下面的定理：

定理：gcd(a,b) = gcd(b,a mod b)

证明：a可以表示成a = kb + r，则r = a mod b
假设d是a,b的一个公约数，则有
d|a, d|b，而r = a - kb，因此d|r
因此d是(b,a mod b)的公约数

假设d 是(b,a mod b)的公约数，则
d | b , d |r ，但是a = kb +r
因此d也是(a,b)的公约数

因此(a,b)和(b,a mod b)的公约数是一样的，其最大公约数也必然相等，得证。

欧几里德算法就是根据这个原理来做的，其算法用C++语言描述为：

void swap(int & a, int & b)

int c = a;
a = b;
b = c;

int gcd(int a,int b)

if(0 == a )

return b;

if( 0 == b)

return a;

if(a > b)

swap(a,b);

int c;
for(c = a % b ; c > 0 ; c = a % b)

a = b;
b = c;

return b;

参考资料：internet 参考技术A 欧几里德算法
欧几里德算法又称辗转相除法，用于计算两个整数a,b的最大公约数。其计算原理依赖于下面的定理：

定理：gcd(a,b) = gcd(b,a mod b)

证明：a可以表示成a = kb + r，则r = a mod b
假设d是a,b的一个公约数，则有
d|a, d|b，而r = a - kb，因此d|r
因此d是(b,a mod b)的公约数

假设d 是(b,a mod b)的公约数，则
d | b , d |r ，但是a = kb +r
因此d也是(a,b)的公约数

因此(a,b)和(b,a mod b)的公约数是一样的，其最大公约数也必然相等，得证

欧几里德算法就是根据这个原理来做的，其算法用C++语言描述为：

void swap(int & a, int & b)

int c = a;
a = b;
b = c;

int gcd(int a,int b)

if(0 == a )

return b;

if( 0 == b)

return a;

if(a > b)

swap(a,b);

int c;
for(c = a % b ; c > 0 ; c = a % b)

a = b;
b = c;

return b;


模P乘法逆元
对于整数a、p，如果存在整数b，满足ab mod p =1，则说，b是a的模p乘法逆元。

定理：a存在模p的乘法逆元的充要条件是gcd(a,p) = 1

证明：
首先证明充分性
如果gcd(a,p) = 1，根据欧拉定理，aφ(p) ≡ 1 mod p，因此
显然aφ(p)-1 mod p是a的模p乘法逆元。

再证明必要性
假设存在a模p的乘法逆元为b
ab ≡ 1 mod p
则ab = kp +1 ，所以1 = ab - kp
因为gcd(a,p) = d
所以d | 1
所以d只能为1

扩展欧几里德算法
扩展欧几里德算法不但能计算(a,b)的最大公约数，而且能计算a模b及b模a的乘法逆元，用C语言描述如下：

int gcd(int a, int b , int& ar,int & br)

int x1,x2,x3;
int y1,y2,y3;
int t1,t2,t3;
if(0 == a)
//有一个数为0，就不存在乘法逆元
ar = 0;
br = 0 ;
return b;

if(0 == b)

ar = 0;
br = 0 ;
return a;

x1 = 1;
x2 = 0;
x3 = a;
y1 = 0;
y2 = 1;
y3 = b;
int k;
for( t3 = x3 % y3 ; t3 != 0 ; t3 = x3 % y3)

k = x3 / y3;
t2 = x2 - k * y2;
t1 = x1 - k * y1;
x1 = y1;
x1 = y2;
x3 = y3;
y1 = t1;
y2 = t2;
y3 = t3;

if( y3 == 1)

//有乘法逆元
ar = y2;
br = x1;
return 1;
else
//公约数不为1，无乘法逆元
ar = 0;
br = 0;
return y3;



扩展欧几里德算法对于最大公约数的计算和普通欧几里德算法是一致的。计算乘法逆元则显得很难明白。我想了半个小时才想出证明他的方法。

首先重复拙作整除中的一个论断：

如果gcd(a,b)=d，则存在m,n，使得d = ma + nb，称呼这种关系为a、b组合整数d，m，n称为组合系数。当d=1时，有 ma + nb = 1 ，此时可以看出m是a模b的乘法逆元，n是b模a的乘法逆元。

为了证明上面的结论，我们把上述计算中xi、yi看成ti的迭代初始值，考察一组数(t1,t2,t3)，用归纳法证明：当通过扩展欧几里德算法计算后，每一行都满足a×t1 + b×t2 = t3

第一行：1 × a + 0 × b = a成立
第二行：0 × a + 1 × b = b成立
假设前k行都成立，考察第k+1行
对于k-1行和k行有
t1(k-1) t2(k-1) t3(k-1)
t1(k) t2(k) t3(k)
分别满足：
t1(k-1) × a + t2(k-1) × b = t3(k-1)
t1(k) × a + t2(k) × b = t3(k)
根据扩展欧几里德算法，假设t3(k-1) = j t3(k) + r
则：
t3(k+1) = r
t2(k+1) = t2(k-1) - j × t2(k)
t1(k+1) = t1(k-1) - j × t1(k)
则
t1(k+1) × a + t2(k+1) × b
=t1(k-1) × a - j × t1(k) × a +
t2(k-1) × b - j × t2(k) × b
= t3(k-1) - j t3(k) = r
= t3(k+1)
得证
因此，当最终t3迭代计算到1时，有t1× a + t2 × b = 1，显然，t1是a模b的乘法逆元，t2是b模a的乘法逆元。 参考技术B 欧几里德算法
欧几里德算法又称辗转相除法，用于计算两个整数a,b的最大公约数。其计算原理依赖于下面的定理：

定理：gcd(a,b) = gcd(b,a mod b)

证明：a可以表示成a = kb + r，则r = a mod b
假设d是a,b的一个公约数，则有
d|a, d|b，而r = a - kb，因此d|r
因此d是(b,a mod b)的公约数

假设d 是(b,a mod b)的公约数，则
d | b , d |r ，但是a = kb +r
因此d也是(a,b)的公约数

因此(a,b)和(b,a mod b)的公约数是一样的，其最大公约数也必然相等，得证

欧几里德算法就是根据这个原理来做的，其算法用C++语言描述为：

void swap(int & a, int & b)

int c = a;

a = b;

b = c;



int gcd(int a,int b)

if(0 == a )

return b;



if( 0 == b)

return a;



if(a > b)

swap(a,b);



int c;

for(c = a % b ; c > 0 ; c = a % b)

a = b;

b = c;



return b;

参考技术C 欧几里德算法
欧几里德算法又称辗转相除法，用于计算两个整数a,b的最大公约数。其计算原理依赖于下面的定理：

定理：gcd(a,b) = gcd(b,a mod b)

证明：a可以表示成a = kb + r，则r = a mod b
假设d是a,b的一个公约数，则有
d|a, d|b，而r = a - kb，因此d|r
因此d是(b,a mod b)的公约数

假设d 是(b,a mod b)的公约数，则
d | b , d |r ，但是a = kb +r
因此d也是(a,b)的公约数

因此(a,b)和(b,a mod b)的公约数是一样的，其最大公约数也必然相等，得证