本周推荐 | AB实验低响应情景解决实践
Posted 阿里巴巴淘系技术团队官网博客
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了本周推荐 | AB实验低响应情景解决实践相关的知识,希望对你有一定的参考价值。

推荐语:本文针对AB实验低响应情景下的增量效果不显著问题,提出通过倾向得分匹配方案来衡量策略增量效果的方法,并将相关方案融入一休平台科学评估体系中。文章理论与实践相结合,深入浅出,强烈推荐。
——大淘宝技术数据研发工程师 伯略

简介
在日常的AB实验情景中,业务通常会遇到策略实际干预人群占分桶人群比例较低的问题,这通常会导致策略效果业务效果不明显以及统计检验难以判断是否显著等问题。作者对低响应实验的定义、影响以及可能的解决方案进行了梳理、介绍和分析,并基于仿真模拟数据和实际线上实验数据进行效果测试。核心结论如下:(1)对于业务效果不显著问题,通过最基础的工具变量方法估计可以一定程度上解决;优化后的倾向得分匹配方案也能较好地解决但需要以一定的偏误为代价(直接应用倾向得分匹配可以在单一场景做针对性优化,但作为通用化的解决方案难度较大);(2)对于统计效果不显著问题,如果在工具变量应用中能够找到合适的协变量则能够有一定程度的解决;优化后的倾向得分匹配方案也能较好地解决,但仍以一定的偏误为代价。

低响应实验介绍
▐ 低响应实验的定义
在AB实验中,由于工程链路、业务要求、策略效果等因素导致样本分流的节点与策略生效的节点存在较大漏损,导致仅有少量用户实际被策略触达,这类实验称为低响应实验。在实际业务中存在很多典型例子,例如:在淘宝首页POP干预促活实验中,由于AB分流是在用户进入首页时触发的,但用户实际被策略影响(曝光或点击POP)受算法调控、用户选择的影响,最终实际被策略触达的人可能不到分桶用户的10%,从而导致策略效果被大幅稀释。
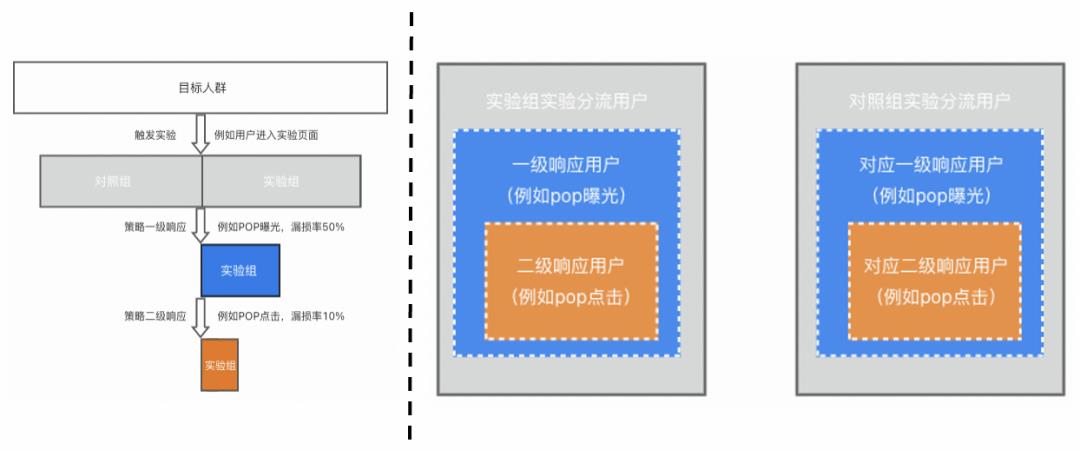
图一:实验链路及样本构成
上图相对清晰地展示了一个低响应实验的样本构成。为方便理解,本文将以淘宝pop干预促活实验为例进行分析:
该实验的分流节点为用户进入淘宝首页时,所以实验组、对照组实验分流用户为各自分桶进入首页的用户
受pop疲劳度算法控制等因素的影响,实验组仅有部分用户成功被pop曝光,这构成了该实验的第一个响应漏斗(首页->曝光);对照组在“平行世界”存在对应的一批用户也被pop曝光
对于pop曝光用户,用户将根据个人喜好选择是否点击pop,这构成了该实验的第二个响应漏斗(曝光->点击);对照组在“平行世界”存在对应的一批用户也会点击pop
仔细分析第一个漏斗不难发现,假如分流可以做到调用pop曝光这个时间节点,该漏斗将不再存在。此外,这部分漏损的用户并未受到策略的影响。本文将这类漏斗称为“实验能力”漏斗(即因为实验设计、工程能力等导致的漏斗)。对于曝光->点击,该漏斗是由用户自身选择导致的,且无法排除漏损用户(曝光->未点击)不会受到策略的影响,本文将这类漏斗称为“用户选择”漏斗。大部分实验的漏斗基本都可以抽象为以上两层,对于“实验能力”漏斗造成的影响需要尽可能地解决,对于“用户选择”漏斗造成的影响则需要结合具体业务场景进行判断,并非所有情况都需要解决。即有时“用户选择”漏斗不算漏斗,其为策略效果的一部分。
▐ 低响应实验的影响
低响应实验的影响可以概括为两方面:(1)降低指标的业务显著性;(2)降低指标的统计显著性。业务显著性降低指指标的均值因为一部分用户为未被策略干预而拉低;统计显著性降低指由于引入了一部分不含任何增量信息的样本(即引入噪声),导致判断指标是否有增量的灵敏度降低(即统计检验的power降低)。
为方便后续的说明,首先对实验样本的相关指标进行定义。
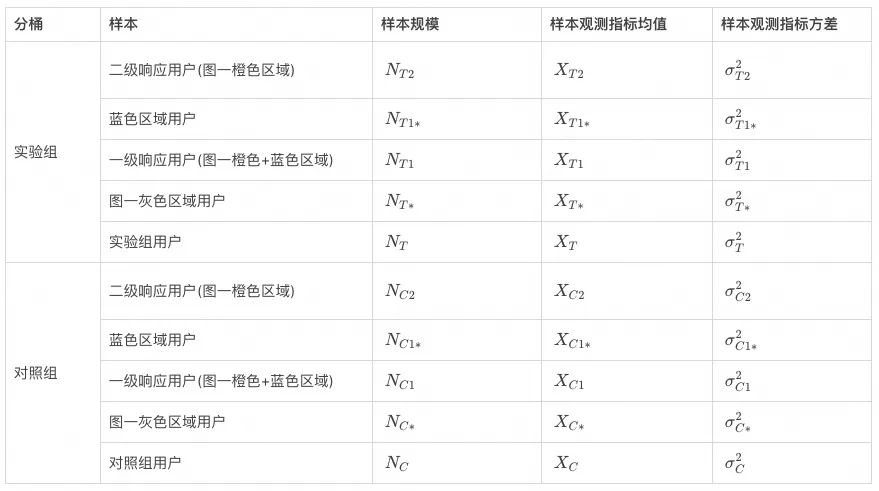
业务显著性
以“实验能力”漏斗为例(首页->曝光):
基于分桶用户计算的策略增量为:
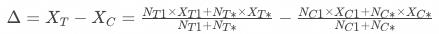
基于一级响应用户计算的策略增量为:
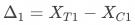
为方便讨论,假设各指标方差为0,实验组与对照组一级响应率相等且为
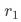 (期望形式的结果类似)
(期望形式的结果类似)根据“实验漏斗的定义”有:
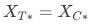
此时,
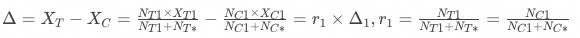
通过上述公式可以发现,一级响应率越低,基于分桶用户计算的策略增量相对于基于一级响应用户计算的增量越小,即指标均值增量被稀释的越严重、业务效果越不显著。
对于“用户选择”漏斗,由于实验组与对照组蓝色区域用户的差异不一定为0,这部分用户本身也反映了策略的效果,在评估策略效果时需要将这部分效果计入在内,因此不存在稀释效果的问题。仅在策略不会对蓝色区域用户产生作用时,解决“用户选择”漏斗才具备实际意义。
统计显著性
仍以“实验能力”漏斗为例(首页->曝光),基于分桶用户计算的策略增量 的方差为:
的方差为: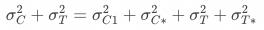 (假设实验组与对照组指标均值协方差为0),基于一级响应用户计算的策略增量
(假设实验组与对照组指标均值协方差为0),基于一级响应用户计算的策略增量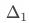 的方差为
的方差为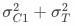 。由于方差大于0,因此基于分桶用户计算的策略增量的波动大于基于一级响应用户计算的策略增量的波动,导致统计上不易判断增量是否显著。
。由于方差大于0,因此基于分桶用户计算的策略增量的波动大于基于一级响应用户计算的策略增量的波动,导致统计上不易判断增量是否显著。
从统计检验的角度看,在一定的假设条件下,假设不存在“实验能力”漏斗时需要的最小样本量为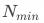 ,则实验漏斗为
,则实验漏斗为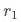 时需要的最小实验量大致为
时需要的最小实验量大致为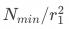 ,即当实验漏斗为10%时,需要的最小样本量会变大100倍。反过来讲,如果实验可用样本量不变,统计检验的灵敏度会相应下降。
,即当实验漏斗为10%时,需要的最小样本量会变大100倍。反过来讲,如果实验可用样本量不变,统计检验的灵敏度会相应下降。

低响应解决方案概览
不同的应用场景、不同的实验问题适用的方案有所差异。本文针对已了解的方案进行了梳理,大致可分为以下几类方案:
低响应解决方案 | 通过工程链路和数据底层改造将AB分流节点后移 | 不含协变量的工具变量估计 | 含协变量的工具变量估计 | 基于倾向得分匹配获得同质人群 |
是否可降低“实验能力”漏斗 | 是 | 是 | 是 | 是 |
如果有必要,是否可降低“用户选择”漏斗 | 否 | 是 | 是 | 是 |
是否能提升业务显著性 | 是 | 是 | 是 | 是 |
是否能提升统计显著性 | 是 | 否 | 是 | 是 |
评估结果是否大样本一致 | 是 | 是 | 大概率否 | 极大概率否 |
备注 | 需要从整个数据底层改造AB实验能力,工程量较大 | 想要获得一致的估计结果需要获得符合假设的协变量,一般情况下是非常困难的 | 存在未控制的混杂变量导致估计结果不一致,理论上不可能控制住所有的混杂变量 |
▐ 通过工程链路和数据底层改造将AB分流节点后移
该方案核心是针对漏斗产生的原因通过工程手段直接解决。以首页POP为例,对于“实验能力”漏斗这类因为分流节点未做到极致的情况,我们确实可以将分流节点从用户进入首页后移至用户将要曝光pop时(调用pop曝光时),但用户是否点击pop受到用户个人选择的影响,我们不能在用户点了领取红包的pop后因为他在对照组而不发放红包。因此,该方案可以降低“实验能力”漏斗,但难以降低“用户选择”漏斗。
▐ 工具变量估计
工具变量估计在经济、医学、生物领域有着广泛的应用,但通常面临着找不到合适的“工具变量”的问题。互联网场景下的AB实验为该方案提供了一个天然有效的工具变量(分桶变量),因此该方案具备通用化应用的可能。不含协变量的工具变量估计因为没有提供额外信息,所以理论上不会降低信噪比而提升统计检验灵敏度。引入协变量后的工具变量估计虽然提供了额外的信息可以提升检验灵敏度,但提供了未控制混杂变量对策略变量评估效果的影响路径,因此会导致估计结果不一致。
▐ 基于倾向得分匹配获得同质人群
AB实验的基础之一是对比的两个样本性质相同,因此对比得到的增量可归因为策略增量。类似的,当实验出现漏斗时,我们如果能够找到策略实际干预人群的同质人群,那么由此计算的增量也可归因为策略增量。为了获得同质人群,虽然我们可在众多维度上保持人群同质,但理论上我们无法控制住所有的混杂因素。因此,评估结果与真实值会存在偏差。
基于倾向得分匹配获得同质人群的估计方案由于引入了大量变量寻找同质人群,因而很难阻断未控制混杂因素通过这些变量对策略变量产生影响。与之不同,含协变量的工具变量估计方案可以只引入一个协变量,更容易阻断未控制混杂因素对策略变量产生影响,因而在提升统计显著性的同时更容易获得一致的评估结果。

工具变量与潜在结果分析框架
▐ 工具变量介绍
通常情况下,当我们直接分析因素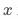 对
对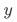 的影响时,我们往往得到的是相关性结论。之所以会这样,是因为其他影响
的影响时,我们往往得到的是相关性结论。之所以会这样,是因为其他影响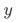 的因素
的因素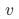 未被控制且这些因素与
未被控制且这些因素与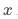 相关,从而导致我们把一部分
相关,从而导致我们把一部分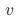 对
对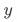 的影响归结到
的影响归结到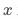 对
对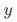 的影响上。上述文字表述,转化成数学公式可表示为:
的影响上。上述文字表述,转化成数学公式可表示为:
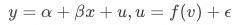
其中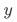 为业务关注的变量(例如,是否来访淘宝),
为业务关注的变量(例如,是否来访淘宝),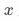 为策略变量(比如是否曝光pop),
为策略变量(比如是否曝光pop),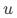 表示所有影响
表示所有影响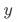 但未控制变量以及噪声的影响。对于上述回归模型,当
但未控制变量以及噪声的影响。对于上述回归模型,当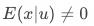 ( 即
( 即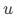 中未控制的变量
中未控制的变量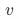 与
与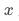 存在相关性)时,常用的估计方案无法得到
存在相关性)时,常用的估计方案无法得到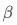 的无偏一致估计,得到的估计值将包含一部分
的无偏一致估计,得到的估计值将包含一部分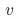 对
对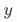 的影响。
的影响。
面对这种情况,在经济、生物、医学存在一种名为“工具变量”的估计方法,该方法指出如果存在一个工具变量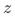 满足以下条件,仍可通过一定方式得到
满足以下条件,仍可通过一定方式得到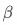 的无偏一致估计:
的无偏一致估计: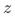 和
和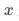 相关;(2)
相关;(2)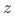 和
和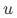 相关;(3)
相关;(3)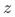 仅通过
仅通过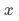 影响
影响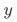 。用图的方式可表示为:
。用图的方式可表示为:
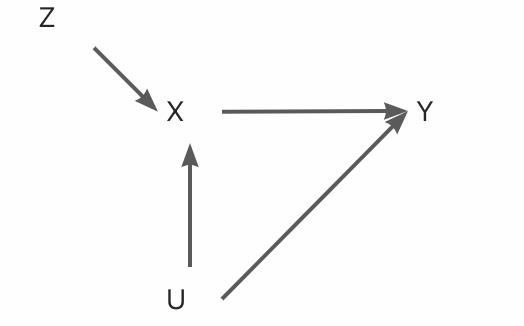
虽然工具变量方法非常简明,但在经济、生医领域一个符合假设要求的工具变量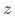 非常难找到。与之不同,互联网的AB场景中,分桶变量(属于实验组为1,对照组为0)是一个完美的工具变量。以首页pop这个实验为例,假如我们关注的是用户是否曝光pop对用户来访淘宝的影响:(1)分桶变量
非常难找到。与之不同,互联网的AB场景中,分桶变量(属于实验组为1,对照组为0)是一个完美的工具变量。以首页pop这个实验为例,假如我们关注的是用户是否曝光pop对用户来访淘宝的影响:(1)分桶变量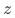 与用户是否曝光pop(
与用户是否曝光pop(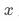 )相关(因为只有实验组的用户才会曝光pop);(2)分桶变量
)相关(因为只有实验组的用户才会曝光pop);(2)分桶变量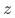 与
与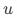 无关,因为分桶是随机的;(3)分桶变量
无关,因为分桶是随机的;(3)分桶变量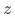 仅通过影响用户曝光对用户淘宝来访产生影响,因为分流->曝光pop漏损的用户实际没有受到策略影响。因为满足工具变量的每个要求,所以分桶变量是一个合理的工具变量。当我们关注的是点击pop对用户来访淘宝的影响时,分桶变量可能不再是一个合适的工具变量。对于前两个假设要求,分桶变量仍旧满足。但对于第三个要求,如果图一蓝色区域的用户因为pop曝光受到了影响,此时
仅通过影响用户曝光对用户淘宝来访产生影响,因为分流->曝光pop漏损的用户实际没有受到策略影响。因为满足工具变量的每个要求,所以分桶变量是一个合理的工具变量。当我们关注的是点击pop对用户来访淘宝的影响时,分桶变量可能不再是一个合适的工具变量。对于前两个假设要求,分桶变量仍旧满足。但对于第三个要求,如果图一蓝色区域的用户因为pop曝光受到了影响,此时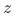 除了通过
除了通过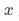 (点击pop)影响
(点击pop)影响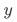 以外,还可以通过曝光pop影响
以外,还可以通过曝光pop影响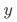 ,那么第三个条件不再满足。所以,此时分桶变量不再是一个合理的工具变量。
,那么第三个条件不再满足。所以,此时分桶变量不再是一个合理的工具变量。
▐ 不含协变量的工具变量估计结果
在互联网AB场景的应用中,由于工具变量是二值变量,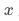 通常也是个二值变量(例如是否曝光pop),此时
通常也是个二值变量(例如是否曝光pop),此时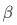 基于工具变量的估计结果非常简单且符合直觉。
基于工具变量的估计结果非常简单且符合直觉。
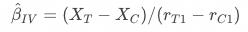
其中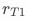 表示实验组pop曝光的响应率,
表示实验组pop曝光的响应率,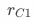 表示对照组pop曝光的响应率。对于上述提到的首页pop促活实验,由于对照组不会曝光pop,所以
表示对照组pop曝光的响应率。对于上述提到的首页pop促活实验,由于对照组不会曝光pop,所以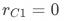 。该估计结果可由2SLS等相对通用的估计方法得到,但在
。该估计结果可由2SLS等相对通用的估计方法得到,但在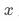 和
和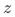 均为二值变量时,有一种更为简单的理解方式。根据增量的定义有:
均为二值变量时,有一种更为简单的理解方式。根据增量的定义有:
增量=实验组pop曝光用户的增量+实验组灰色区域用户的增量
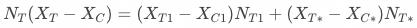
根据工具变量的第3点假设有
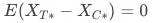 ,所以大致有
,所以大致有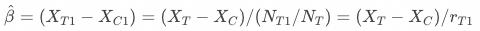
至此,我们已经能够获得策略变量对关注指标的效果,在互联网AB场景下,它等于响应用户在观测指标均值上的增量除以实验组用户的响应率(对于更一般的场景是增量响应率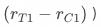 。看似我们已经解决了低响应问题业务显著性的问题,但实际上并不完全。识别的增量对应哪群用户?是否在策略推全后仍然有这么多的增量?这些问题我们并不清楚。
。看似我们已经解决了低响应问题业务显著性的问题,但实际上并不完全。识别的增量对应哪群用户?是否在策略推全后仍然有这么多的增量?这些问题我们并不清楚。
▐ 不含协变量的工具变量估计与潜在结果分析框架
因果效应通俗地理解就是假如同一个人做了某件事和没做某件事他在观测指标上有何差异。基于潜在结果分析框架,我们定义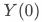 、
、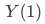 为用户在未响应策略、响应策略(曝光pop、点击pop)时观测指标的结果;
为用户在未响应策略、响应策略(曝光pop、点击pop)时观测指标的结果;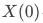 、
、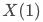 为用户在对照组和实验组时策略响应的情况。
为用户在对照组和实验组时策略响应的情况。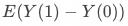 通常称作ATE(平均处理效应),即用户在策略上的平均处理效果,对其展开有:
通常称作ATE(平均处理效应),即用户在策略上的平均处理效果,对其展开有:
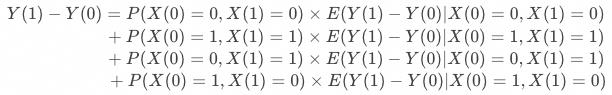
可以发现,ATE是由四类用户的处理效应构成的(由于是部分用户的效应,所以也称做LATE即局部平均处理效应):
永不响应用户
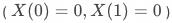 ,即不管有无策略干预,总不响应
,即不管有无策略干预,总不响应总是响应用户
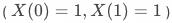 ,即不管有无策略干预,总是响应
,即不管有无策略干预,总是响应顺从用户
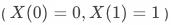 ,即受实验干预时响应,否则不响应
,即受实验干预时响应,否则不响应对抗用户
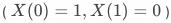 ,即受实验干预时不响应,否则响应
,即受实验干预时不响应,否则响应
在实际实验的增量中,由于永不响应用户、总是响应用户不贡献增量,所以实验观测到的增量由顺从用户与对抗用户提供。假设实验中不存在对抗用户
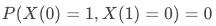
则增量公式可变形为:
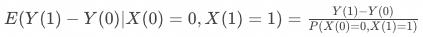
不难发现,上式等式右侧就是工具变量的估计结果。即假如不存在对抗用户,工具变量估计的实际是顺从用户在策略上的增量效果。假如存在对抗用户,工具变量实际估计的是顺从用户与对抗用户的平均增量效果:
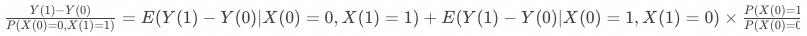
回到首页pop促活实验中,假如策略响应定义为曝光pop,由于一定不存在对抗用户,所以工具变量估计的是顺从用户的增量效果。假如策略响应定义为购买商品,则可能存在对抗者,此时工具变量估计的是顺从用户与对抗用户的平均增量效果。无论是哪种情况,工具变量估计的效果都是业务首先想要知道的,因为业务核心关注的是策略干预的用户带来的效果,既需要涵盖正向效果也不能遗漏可能的负向效果(通常对抗者的效果可能是负向的)。上述得到的效果都是局部平均处理效果,在实际的策略评估中可能希望知道所有用户都受到策略影响时的增量效果,此时涉及LATE->ATE的推断。Heckman等学者在这一领域有过诸多研究,感兴趣的同学可以自行了解。
▐ 含协变量的工具变量估计
基于不含协变量的工具变量已经可以解决低响应实验业务不显著的问题,但无法解决统计显著问题。简单来说,不含协变量的工具变量估计仅提供了识别LATE的信息,除此之外没有提供其他信息,所以统计推断的效率并不会提高。此时,可以通过引入协变量增加信息量提升推断的效率。具体来说,引入协变量后估计方程变为:
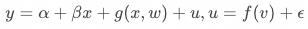
其中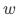 为引入的可观测的协变量。类似对
为引入的可观测的协变量。类似对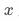 的要求,需要混杂因素无法通过
的要求,需要混杂因素无法通过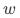 影响
影响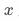 对
对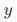 的效应,我们才能获得
的效应,我们才能获得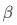 的一致估计结果。然而这样的协变量相对难找,能否找到取决于研究的指标和分析的场景。假如某个实验考虑的是红包策略对饿了么DAU的影响,那么用户所在地的降雨量可能是一个很好的协变量:既影响用户是否来访饿了么,也是个相对外生的变量不受用户自身主观因素的影响。对于淘宝的DAU场景,由于降雨量对用户是否来访淘宝影响可能很弱,降雨量不再是个很好的指标。如果有比较合适的协变量能够引入,则可既解决低响应实验的业务显著问题、也能解决统计显著问题。
的一致估计结果。然而这样的协变量相对难找,能否找到取决于研究的指标和分析的场景。假如某个实验考虑的是红包策略对饿了么DAU的影响,那么用户所在地的降雨量可能是一个很好的协变量:既影响用户是否来访饿了么,也是个相对外生的变量不受用户自身主观因素的影响。对于淘宝的DAU场景,由于降雨量对用户是否来访淘宝影响可能很弱,降雨量不再是个很好的指标。如果有比较合适的协变量能够引入,则可既解决低响应实验的业务显著问题、也能解决统计显著问题。

倾向得分匹配相关方案
▐ 倾向得分匹配简介
倾向得分匹配(PSM)的核心思想是找到策略响应人群的同质人群,通过计算策略响应人群与同质人群在观测指标上的差异获得增量。由于该方法对于技术同学相对熟悉,这里仅做一个简要介绍。倾向得分匹配核心依赖两个假设:
条件独立假设(Conditional Independence Assumption)
用数学公式可表述为:
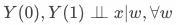
即给定协变量
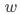 时,用户是否响应策略与潜在结果无关。该假设核心是保证匹配结果的同质性。
时,用户是否响应策略与潜在结果无关。该假设核心是保证匹配结果的同质性。共同支撑假设(Common Support)
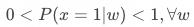
即给定变量
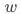 时,用户既可能响应策略也可能不响应策略。该条件保证了可以匹配到响应用户的对应用户
时,用户既可能响应策略也可能不响应策略。该条件保证了可以匹配到响应用户的对应用户
当上述两个条件满足时,经过一定的匹配算法计算我们可以得到策略增量效果。由于并非所有的策略响应用户都能匹配到对应的用户,所以PSM实际计算的是匹配成功用户的策略增量效果,与原本想测算的策略响应用户的增量效果存在一定差异。此外,为获得更为稳健的评估结果,通常会将PSM与DID结合进行计算。
整个的计算过程核心分为两大步骤,第一步为倾向得分的预测,第二步为用户匹配。通常情况下,倾向得分预测实际是一个二分类问题,因此常用的逻辑回归、树等模型均可使用。在得到倾向分后,需要对响应用户匹配对应人群,常用的匹配方式如下。在得到匹配结果后,便可计算出对应的增量效果并进行统计检验。
匹配方式 | 大致逻辑 | 额外说明 |
Nearest Neighbour Matching (最近邻匹配) | 选取倾向得分最近的用户进行匹配 | 为了提升匹配稳定性,可对一定分差范围内的匹配样本做加权平均匹配 |
Caliper and Radius Matching (有边界限制的半径匹配) | 当一定分差范围内没有可以匹配的用户时,最近邻匹配的匹配效果可能较差。此时可以限定一定的匹配范围,对于匹配不上的样本进行丢弃。 | 丢弃样本的方案会导致识别增量的背后含义发生变化,即由全体响应用户的平均增量转变为可匹配用户的平均增量 |
Stratification and Interval Matching (分层区间匹配) | 该方案将倾向得分分成若干区间,然后在相应区间内进行匹配 |
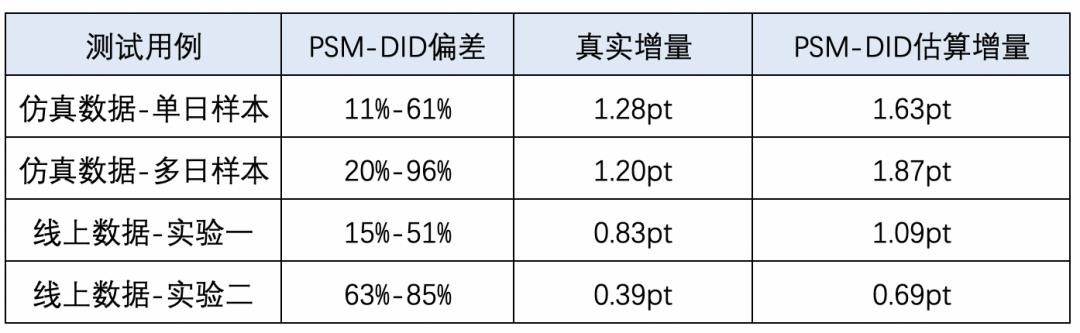
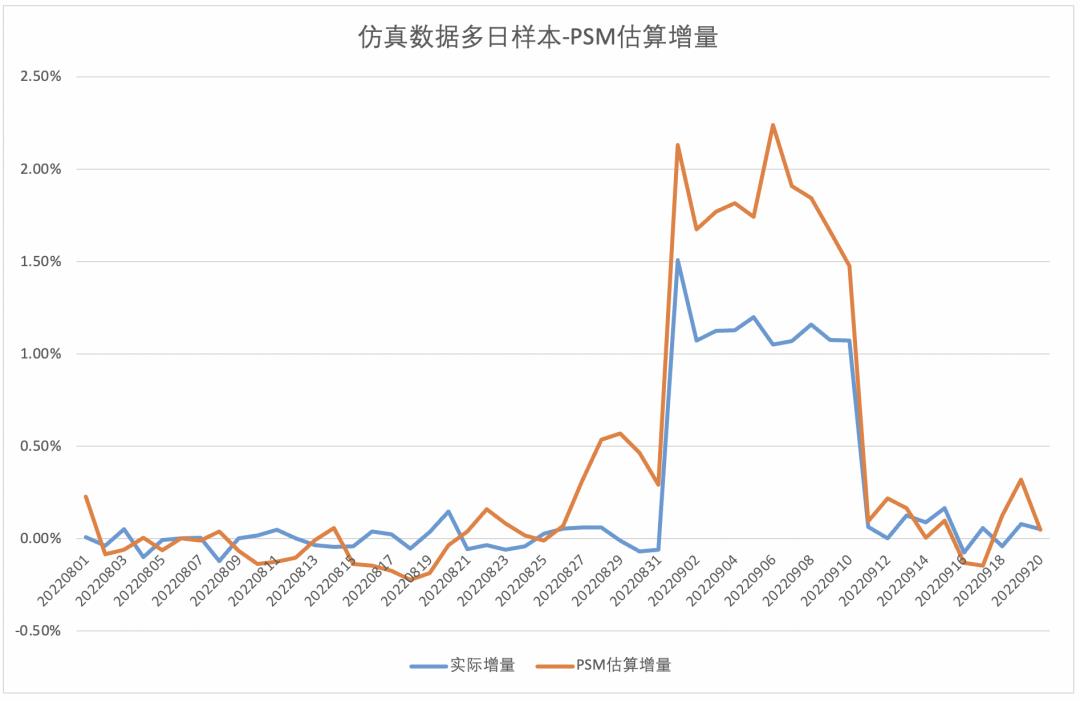
▐ 倾向得分匹配方案测试效果
通过仿真模拟数据和两个实际线上案例测试了倾向得分匹配的效果,实践发现通常情况下倾向得分匹配方案会一定程度地高估增量效果,该原因主要是在倾向得分匹配时遗漏了一部分高活用户的混淆因子。在测试过程中,我们可以针对特定的应用场景进行模型优化将估算偏差降低,但作为通用化的解决方案,直接应用倾向匹配得分方案可能会出现个别场景偏差较大的情况。因此,需要一个更为稳定、精准的解决方法。
▐ 倾向得分匹配方案优化及效果
最初选择测试PSM及相关方案解决低响应问题本希望的是通过尽可能丰富、有效的特征贴近CIA假设,从而得到一个尽可能一致的估计结果。然而在实践过程中发现,由于CIA假设不可能严格满足,所以PSM计算的增量结果多少都会有一定偏误且个别场景可能会出现偏差较大的问题。既然一致估计的目的无法实现,退而求其次可以选择其他的解决方案,在一定估计偏误范围内,尽可能地降低噪声、提升方案稳定性、增强统计检验灵敏度。
通常PSM的应用多是基于观察性数据,受到干预的用户与可匹配用户本身存在天然不同。但在AB实验场景中,天然的存在两群同质用户,即对照组和实验组。此时,我们可以不再从实验组未受到干预的用户中寻找同质人群,而是从对照组中寻找同质人群(实际上也确实存在)。此外,对于倾向得分较低的用户,其受到策略干预相对更为随机(例如误触),为其匹配同质人群的难度更大也更容易引起偏误。基于上述两点,我们可以丢弃一部分倾向得分较低的用户不再匹配,并对剩余样本采用分群匹配的方案以充分利用AB实验提供的人群同质基础。
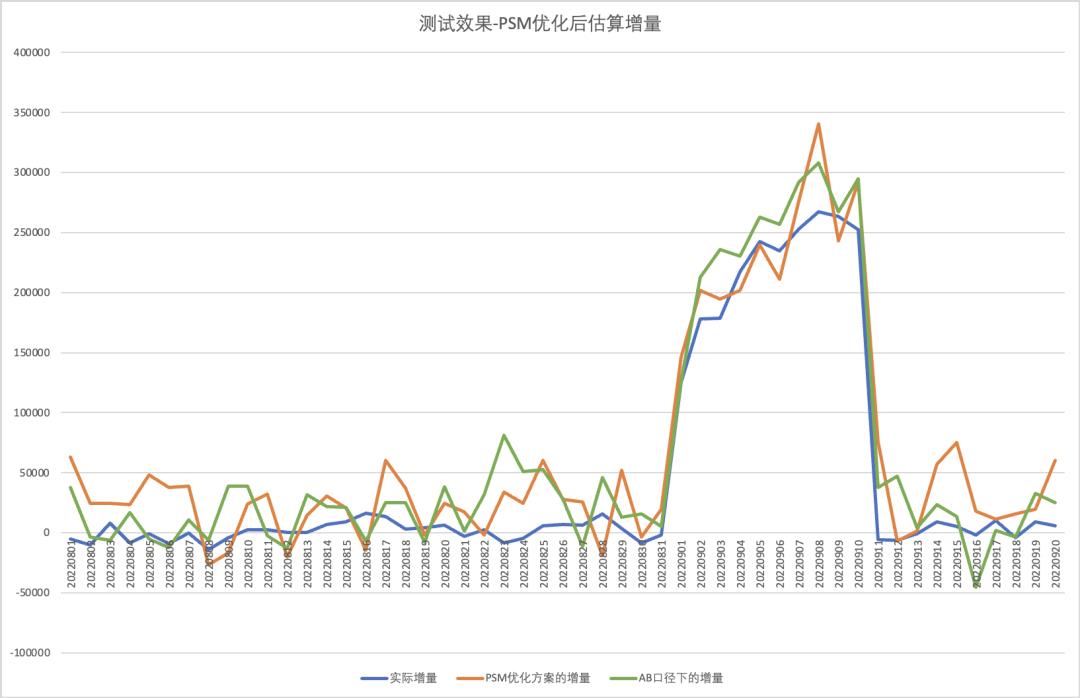
基于上述改进后的方案,利用测试数据进行测试,实际效果如下表格和图。由表可知,相较于AB口径,优化后的倾向得分匹配方案相较AB口径在指标均值、统计检验上更为显著。从图中可以看到,优化后的PSM方案增量估计结果、变动趋势与实际值基本一致,因此通过该方案可以相对准确、稳定的估算增量结果。
方案 | 实验周期内指标均值 日均增量 | 实验周期内指标规模 日均增量 | 实验周期内显著天数 | 实验周期内日均指标 统计检验是否显著 |
AB口径 | 0.049pt | 24.8w | 2/10 | 否 |
优化后倾向得分匹配 | 0.288pt | 20.8w | 9/10 | 是 |
优化后的倾向得分匹配方案已经融入一休平台科学评估体系中,若有使用需要可以联系平台相关同学。

总结
对于业务效果不显著问题,通过最基础的工具变量方法估计可以一定程度上解决;优化后的倾向得分匹配方案也能较好地解决但需要以一定的偏误为代价。
对于统计效果不显著问题,如果在工具变量应用中能够找到合适的协变量则能够有一定程度的解决;优化后的倾向得分匹配方案也能较好地解决,但仍以一定的偏误为代价。
响应程度的高低取决于我们认为策略从何时产生作用,不同的响应定义对应不同的增量含义;只有当漏斗能够通过一定策略、工程手段避免时,该漏斗才应该考虑通过数据手段修正以降低对实验评估产生影响。

团队介绍
大淘宝技术用户平台数据洞察团队,负责淘宝用户增长、私域、会员、互动业务的“人”“货”“场”的分析建模、运营策略洞察,为千万级 DAU 增量目标提供运营策略支持,为订阅、店铺等私域场景定义优质店铺标准和内容优选策略,科学衡量数亿“人店”关系的质量,同时参与 88VIP、省钱月卡、淘金币等会员和货币流通体系设计,以及淘宝互动游戏的潜客挖掘、分层运营、促活促购策略优化。团队目前有数据科学岗位杭州 hc,欢迎加入,一起为淘宝核心业务的增长做出贡献!简历投递邮箱:youchen.wtx@alibaba-inc.com。
¤ 拓展阅读 ¤
以上是关于本周推荐 | AB实验低响应情景解决实践的主要内容,如果未能解决你的问题,请参考以下文章