平衡树的主要算法

Posted 2023-04-23

参考技术A

红黑树的平衡是在插入和删除的过程中取得的。对一个要插入的数据项，插入程序要检查不会破坏树一定的特征。如果破坏了，程序就会进行纠正，根据需要更改树的结构。通过维持树的特征，保持了树的平衡。
红黑树有两个特征：
(1) 节点都有颜色
(2) 在插入和删除过程中，要遵循保持这些颜色的不同排列的规则。
红黑规则：
1. 每一个节点不是红色的就是黑色的
2. 根总是黑色的
3. 如果节点是红色的，则它的子节点必须是黑色的（反之不一定成立）
4. 从根到叶节点或空子节点的每条路径，必须包含相同数目的黑色节点。
（空子节点是指非叶节点可以接子节点的位置。换句话说，就是一个有右子节点的节点可能接左子节点的位置，或是有左子节点的节点可能接右子节点的位置） AVL树，它或者是一颗空二叉树，或者是具有下列性质的二叉树：
(1) 其根的左右子树高度之差的绝对值不能超过1；
(2) 其根的左右子树都是二叉平衡树。
AVL树查找的时间复杂度为O(logN)，因为树一定是平衡的。但是由于插入或删除一个节点时需要扫描两趟树，依次向下查找插入点，依次向上平衡树，AVL树不如红黑树效率高，也不如红黑树常用。
AVL树插入的C++代码： template<classT>ResultCodeAVLTree<T>::Insert(AVLNode<T>*&p,T&x,bool&unBalanced)...ResultCoderesult=Success;if(p==null)...//插入新节点p=newAVLNode<T>(x);unBalanced=true;elseif(x<p->element)...//新节点插入左子树result=Insert(p->lChild,x,unBalanced);if(unBanlanced)...switch(p->bF)...case-1:p->bF=0;unBalanced=false;break;case0:p->bF=1;break;case1:LRotation(p,unBalanced);elseif(x==p->element)...//有重复元素，插入失败unBalanced=false;x=p->element;result=Duplicate;else...//新节点插入右子树result=Insert(p->rChild,x,unBalanced);if(unBalanced)...switch(p->bF)...case1:p->bF=0;unBalanced=false;break;case0:p->bF=-1;break;case-1:RRotation(p,unBalanced);returnresult;template<classT>voidAVLTree<T>::LRotation(AVLNode<T>*&s,bool&unBalanced)...AVLNode<T>*u,*r=s->lChild;if(r->bF==1)...//LL旋转s->lChild=r->rChild;r->rChild=s;s->bF=0;s=r;//s指示新子树的根else...//LR旋转u=r->rChild;r->rChild=u->lChild;u->lChild=r;s->lChild=u->rChild;u->rChild=s;switch(u->bF)...case1:s->bF=-1;r->bF=0;break;case0:s->bF=r->bF=0;break;case-1:s->bF=0;r->bF=1;s=u;//s指示新子树的根s->bF=0;//s的平衡因子为0unBalanced=false;//结束重新平衡操作通常我们使用二叉树的原因是它可以用O（logn）的复杂度来查找一个数，删除一个数，对吧？？可是有时候会发现树会退化，这个就可能使O（logn）->O（n）的了，那么还不如用直接搜一次呢！！所以我们就要想办法使一棵树平衡。而我仅仅看了（AVL）的那个，所以也仅仅能说（AVL）的那个，至于（TREAP），我还不懂，如果你们知道算法的话，欢迎告诉我~！谢谢~
首先引入一个变量，叫做平衡因子（r），节点X的r就表示x的左子树的深度-右子树的深度。然后我们要保证一棵树平衡，就是要保证左右子树的深度差小于等于1.所以r的取值能且仅能取0，-1，1.
其次，我要介绍旋转，旋转有两种方式，就是左旋（顺时针旋转）和右旋（逆时针旋转）。
左旋（左儿子代替根）：即用左儿子取代根，假设我们要旋转以X为根，LR分别为X的左右儿子，那么我们只需要把L的右儿子取代X的左儿子，然后把更新后的X赋值为L的右儿子，就可以了。
右旋（右儿子代替根）：即用右儿子取代根，假设我们要旋转以X为根，LR分别为X的左右儿子，那么我们只需要把R的左儿子取代X的右儿子，然后把更新后的X赋值为R的左儿子，就可以了。 Size Balanced Tree(SBT平衡树）是2007年Winter Camp上由我国著名OI选手陈启峰发布的他自己创造的数据结构。相比于一般的平衡树，此平衡树具有的特点是：快速（远超Treap，超过AVL)、代码简洁、空间小（是线段树的1/4左右）、便于调试和修改等优势。
与一般平衡搜索树相比，该数据结构只靠维护一个Size来保持树的平衡，通过核心操作Maintain(修复）使得树的修改平摊时间为O(1)。因而大大简化代码实现复杂度、提高运算速度。
参见百度百科SBT。 平衡树的一种，每次将待操作节点提到根，每次操作时间复杂度为O(logn)。见伸展树。 constintSPLAYmaxn=200005;constintSPLAYinf=100000000;structSplay_Nodeintl,r,fa,v,sum;;structSplaySplay_Nodet[SPLAYmaxn];introot,tot;voidcreate()root=1,tot=2;t[1].v=-SPLAYinf;t[2].v=SPLAYinf;t[1].r=t[1].sum=2;t[2].fa=t[2].sum=1;voidupdate(intnow)t[now].sum=t[t[now].l].sum+t[t[now].r].sum+1;voidleft(intnow)intfa=t[now].fa;t[now].fa=t[fa].fa;if(t[t[fa].fa].l==fa)t[t[fa].fa].l=now;if(t[t[fa].fa].r==fa)t[t[fa].fa].r=now;t[fa].fa=now;t[fa].r=t[now].l;t[t[now].l].fa=fa;t[now].l=fa;up(fa);voidright(intnow)intfa=t[now].fa;t[now].fa=t[fa].fa;if(t[t[fa].fa].l==fa)t[t[fa].fa].l=now;if(t[t[fa].fa].r==fa)t[t[fa].fa].r=now;t[fa].fa=now;t[fa].l=t[now].r;t[t[now].r].fa=fa;t[now].r=fa;update(fa);voidsplay(intnow,intFA=0)while(t[now].fa!=FA)intfa=t[now].fa;if(t[fa].fa==FA)if(t[fa].l==now)right(now);elseleft(now);elseif(t[t[fa].fa].l==fa)if(t[fa].l==now)right(fa),right(now);elseleft(now),right(now);elseif(t[fa].l==now)right(now),left(now);elseleft(fa),left(now);update(now);if(!FA)root=now;intlower_bound(intv)intans=0,la=0;for(intnow=root;now;)la=now;if(t[now].v>=v)ans=now,now=t[now].l;elsenow=t[now].r;splay(la);returnans;voidinsert(intv)for(intnow=root;;)++t[now].sum;if(t[now].v>=v)if(t[now].l)now=t[now].l;elset[now].l=++tot;t[tot].sum=1;t[tot].fa=now;t[tot].v=v;splay(tot);return;elseif(t[now].r)now=t[now].r;elset[now].r=++tot;t[tot].sum=1;t[tot].fa=now;t[tot].v=v;splay(tot);return;intget_lower(inta)splay(a);for(a=t[a].l;t[a].r;a=t[a].r);returna;intget_upper(inta)splay(a);for(a=t[a].r;t[a].l;a=t[a].l);returna;intget_rank(inta)splay(a);returnt[t[a].l].sum;voiddel(intl,intr)l=get_lower(l);r=get_upper(r);splay(l);splay(r,l);t[r].l=0;update(r);update(l);intget_kth(intk)++k;for(intnow=root;;)if(t[t[now].l].sum==k-1)returnnow;if(t[t[now].l].sum>=k)now=t[now].l;elsek-=t[t[now].l].sum+1,now=t[now].r;;

浅析AVL树算法

AVL树简介

   AVL树是一种高度平衡的二叉树，在定义树的每个结点的同时，给树的每一个结点增加成员 平衡因子bf  ，定义平衡因子为右子树的高度减去左子树的高度。AVL树要求所有节点左右子树的高度差不超过2，即bf的绝对值小于2。

   当我们插入新的结点之后，平衡树的平衡状态将会被破坏，因此我们需要采用相应的调整算法使得树重新回归平衡。

预备知识

    前文说当插入新的结点时，树的结构可能会发生破坏，因此我们设定了一套调整算法。调整可分为两类：一类是结构调整，即改变树中结点的连接关系，另一类是平衡因子的调整，使平衡因子重新满足AVL树的要求。调整过程包含四个基本的操作，左旋转，右旋转，右左双旋，左右双旋。   

平衡树的旋转，目的只有一个，降低树的高度，高度降低之后，就大大简化了在树中查找结点时间复杂度。

左旋：   

10、20为树的三个结点。当在20的右子树插入一个结点之后，如图。当Parent结点的平衡因子为2，cur结点的平衡因子为1时进行左旋。

将 parent 的 right 指针，指向cur 的left结点；同时cur的left 指针，指向parent 结点。cur 结点继承了原来parent结点在该树（子树）中的根节点的位置，如果原来的parent结点还有父结点，cur需要和上一层的结点保持连接关系。（这里我们允许cur的左子树为NULL）

可以看到，旋转之后，原来的parent结点和cur结点的平衡因子都变为0 。

//左旋转代码实现：
	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;	
		
		parent->_right = subRL;
		if (subRL != NULL)
			subRL->_parent = parent;


        Node* ppNode = parent->_parent;
		subR->_left = parent;
		parent->_parent = subR;

		if (ppNode == NULL)
		{
			_root = subR;
			subR->_parent = NULL;
		}
		else
		{
			if (parent == ppNode->_left)
				ppNode->_left = subR;
			if (parent == ppNode->_right)
				ppNode->_right = subR;

			subR->_parent = ppNode;
		}

		parent->_bf = 0;
		subR->_bf = 0;
	}

右旋：

    右旋和左旋的原理类似，和左旋成镜像关系。当parent结点的平衡因子变为 -2，cur结点的平衡因子变为-1 时，进行右旋。

   将 parent 结点的左指针，指向cur结点的右子树，cur结点的右指针，指向parent结点。同时，cur结点将要继承在该子树中parent结点的根节点的位置。即如果parent结点有它自己的父节点，cur将要和parent结点的父节点保持指向关系。（这里同样允许cur的右子树为NULL）

   旋转之后，也可以发现，parent 和 cur结点的平衡因子都变为0。

 

//右旋转代码实现

void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR != NULL)
{
subLR->_parent = parent;
}
Node* ppNode = parent->_parent;
subL->_right = parent;
    parent->_parent = subL;
if (ppNode == NULL)
{
_root = subL;
subL->_parent = NULL;
}
else
{
if (parent == ppNode->_left)
ppNode->_left = subL;
else
ppNode->_right = subL;
           subL->_parent = ppNode;
}
parent->_bf = 0;
subL->_bf = 0;
}

右左双旋：

理解了左单旋和右单旋的情况，双旋实现起来就简单了些。

上图给出了右左双旋的情况，可以看到，当parent 的平衡因子为2，cur 的平衡因子为-1时，满足右左双旋的情况。

右左双旋的实现，可分为三步。

1>以parent->_right 结点为根进行右旋转

2>以parent结点为根进行左旋转

3>进行调整。

前两步应该理解起来问题不大，但右左旋转之后，为什么还要多一步调整呢？原因就在于我的新增结点是在key=20结点（cur结点的左孩子）的左子树还是右子树插入的，还有可能20就是我的新增结点，即h=0。三种情况造成的直接后果就是cur的左孩子结点的平衡因子不同。这将是我们区分三种情况的依据。

这里有个问题值得注意，为了提高代码的复用性，我们在双旋的实现中调用了单旋的函数，但在单旋最后，我们都会将parent 和cur 结点的bf 置0。因此，在单旋之前我们需要保存cur->_left结点的平衡因子。（如上图）

    

//右左旋转
void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
size_t bf = subRL->_bf;
RotateR(parent->_right);
RotateL(parent);
if (bf == 0)
{
parent->_bf = 0;
subR->_bf = 0;
subRL->_bf = 0;
}
else if (bf == 1)
{
subR->_bf = 0;
parent->_bf = -1;
subRL->_bf = 0;
}
else
{
parent->_bf = 0;
subR->_bf = 1;
subRL->_bf = 0;
}
}

左右双旋：

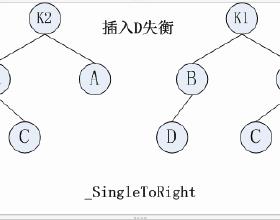
左右双旋和右左双旋其实也差不多，当满足parent的平衡因子为-2，且cur 的平衡因子为1时，进行左右双旋。

和右左双旋的概念类似，我们依旧要先调用单旋函数，之后再进行调整。也需要注意插入节点的位置不同带来的影响，提前对cur的右节点的平衡因子进行保存。这里同样给出图示和代码，不再过多赘述。

//左右双旋
void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
size_t bf = subLR->_bf;
RotateL(parent->_left);
RotateR(parent);
if (bf == 0)
{
parent->_bf = 0;
subL->_bf = 0;
subLR->_bf = 0;
}
else if (bf == 1)
{
parent->_bf = 0;
subL->_bf = -1;
subLR->_bf = 0;
}
else
{
parent->_bf = 1;
subL->_bf = 0;
subLR->_bf = 0;
}
}

插入算法

    首先我们给出结点的定义和相应的构造函数，其中，_key为关键码，_value为值。

template <typename K, typename V>
struct AVLTreeNode
{
int _bf;
K _key;
V _value;
AVLTreeNode<K, V>* _left;
AVLTreeNode<K, V>* _right;
AVLTreeNode<K, V>* _parent;
AVLTreeNode(const K& key, const V& value)
:_bf(0)
, _key(key)
, _value(value)
, _left(NULL)
, _right(NULL)
, _parent(NULL)
{}
};

    接下来我们分析的是插入结点的几种情况：

1、树为空树(_root == NULL）

       给根节点开辟空间并赋值，直接结束

 

if (_root == NULL)
{
_root = new Node(k, v);
return true;
}

2、树不为空树

要在树中插入一个结点，大致可分为几步。

1>   找到该结点的插入位置

2>   插入结点之后，调整该结点与parent结点的指向关系。

3>   向上调整插入结点祖先结点的平衡因子。

 

   由于AVL树是二叉搜索树，通过循环，比较待插入结点的key值和当前结点的大小，找到待插入结点的位置。同时给该节点开辟空间，确定和parent节点的指向关系。

//找到待插入结点位置
Node* cur = _root;
Node* parent = NULL;
while (cur != NULL)
{
parent = cur;
if (k > cur->_key)
{
cur = cur->_right;
}
else if (k < cur->_key)
{
cur = cur->_left;
}
else
{
return false;
}
}
//插入节点，建立指向关系
cur = new Node(k, v);
if (k < parent->_key)
{
parent->_left = cur;
cur->_parent = parent;
}
else
{
parent->_right = cur;
cur->_parent = parent;
}

    插入结点之后，对该AVL树结点的平衡因子进行调整。由于插入一个结点，其祖先结点的循环因子都可能发生改变，所以采用循环的方式，向上调整循环因子。

 

    由上图可知，当插入节点之后，该结点的向上的所有祖先结点的平衡因子并不是都在变化，当向上调整直到某一结点的平衡因子变为 0 之后，将不再向上调整，因为此时再向上的结点的左右子树高度差没有发生变化。

      

       接下来是向上调整平衡因子。

       由于存在要向上调整，这里定义两个指针，parent 指针和 cur 指针。当开始循环之后，首先进行调整 parent 指针的平衡因子。调整之后，判断平衡因子。

平衡因子为 0 ，则直接跳出循环。

平衡因子为 1 或 -1 时，继续向上调整，进行下次循环。

平衡因子为 2 或 -2 时，就要用到我们一开始提到的算法--->平衡树的旋转

while (parent)
{
//调整parent的bf
if (k < parent->_key)
{
parent->_bf--;
}
else
{
parent->_bf++;
}
//如果parent的bf为0，表面插入结点之后，堆parent以上节点的bf无影响
if (parent->_bf == 0)
{
return true;
}
else if (abs(parent->_bf) == 1)  //为1、-1时继续向上调整
{
cur = parent;
parent = cur->_parent;
}
else//2、-2   为2、-2时进行旋转调整
{
if (parent->_bf == 2)
{
if (cur->_bf == 1)
{
RotateL(parent);
break;
}
else if (cur->_bf == -1)
{
RotateRL(parent);
break;
}
}
else//parent->_bf == -2
{
if (cur->_bf == -1)
{
RotateR(parent);
break;
}
else if (cur->_bf == 1)
{
RotateLR(parent);
break;
}
}
}
}

    到这里，插入算法就已经结束，接下来给出两个函数，用以对我们刚刚构建好的AVL树进行判断，看是否满足我们的条件。

bool IsBalance()
{
int sz = 0;
return _IsBalance_better(_root, sz);
}
bool _IsBalance(Node* root,int& height)
{
if (root == NULL)
return true;
int leftheight = 0;
if (_IsBalance(root->_left, leftheight) == false)
return false;
int rightheight = 0;
if (_IsBalance(root->_right, rightheight) == false)
return false;
height = leftheight > rightheight ? leftheight : rightheight;
return abs(leftheight - rightheight) < 2 && (root->_bf == rightheight - leftheight);
}

    关于完整的AVL树的代码，会在下面给出，这里想多说一点的是，AVL树是一棵高度平衡的二叉树，当我们构建好这样一棵二叉树之后，进行查找、插入、删除相应结点的时候，效率肯定是最高的，时间复杂度为O(logN),但实际应用中，比起和他类似的红黑树，AVL的实现难度和由于AVL树的高要求(abs(bf) <2)导致的插入结点要多次调整，AVL树的使用相对较少。

本文出自 “暮回” 博客，请务必保留此出处http://muhuizz.blog.51cto.com/11321490/1867315