SVM中核函数的理解

Posted 2020-11-19 aaron12

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了SVM中核函数的理解相关的知识，希望对你有一定的参考价值。

（1）如何理解核函数能把低维映射到高维

关键：因为有泰勒展开

严格说是为什么高斯核函数能够将低维映射到无穷维

对于高斯核为什么可以将数据映射到无穷多维，我们可以从泰勒展开式的角度来解释，

首先我们要清楚，SVM中，对于维度的计算，我们可以用内积的形式，假设函数：
$技术分享图片$ 表示一个简单的从二维映射到三维。
则在SVM的计算中，可以表示为：
$技术分享图片$

再来看 $技术分享图片$ 泰勒展开式：
$技术分享图片$
所以这个无穷多项的式子正是对于 $技术分享图片$ 的近似， $技术分享图片$ 所对应的映射：
$技术分享图片$

再来看高斯核：
$技术分享图片$

将泰勒展开式带入高斯核，我们得到了一个无穷维度的映射：
$技术分享图片$
那么，对于 $技术分享图片$ 和 $技术分享图片$ 的内积形式符合在SVM中无穷维度下的内积计算，即高斯核将数据映射到无穷高的维度。

链接

（2）为什么更倾向于选高斯核饿函数，而不是多项式核？

结论：多项式核函数可以将原始维度映射到高维，高斯核函数可以将原始维度映射到无穷维

1.先考虑多项式核函数(polynomial kernel)
比如

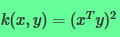
技术分享图片

假设每个向量维度为2 两向量 X = (x1 , y1) Y = (y1 , y2)。
则有:
$技术分享图片$ = $技术分享图片$
找到特征映射 $技术分享图片$ 因为 $技术分享图片$

则 $技术分享图片$ 将 $技术分享图片$ 的点映射到 $技术分享图片$

2.现在分析高斯核

同样每个向量的维度为2 两向量 X = (x1 , y1) Y = (y1 , y2)
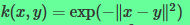
则有
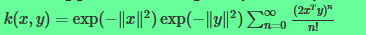
$技术分享图片$ $技术分享图片$

根据泰勒公式

那么

可以看出公式中的的泰勒展开式其实是0-n维的多项式核函数的和。
我们知道多项式核函数将低维数据映射到高维(维度是有限的)，那么对于无限个不同维的多项式核函数之和的高斯核，其中也包括无穷维度的多项式核函数。而且我们也找得到 $技术分享图片$ 使
该等式

$技术分享图片$

成立

而且维度是无穷维。

资料
Why does the RBF (radial basis function) kernel map into infinite dimensional space?

所以这样看来
核函数是一种特殊的多项式核。

（3）几个概念

1）引入kernel的目的不是为了升维，而是升维后的简化计算。

Kernel Function只是一个关于特征向量的函数，本质是变换后的空间中的内积，这个函数的构造和引入的初衷只是为了提高SVM在高维的计算效率。

2）kernel和SVM是两回事，只是刚好在SVM中引入了kernel而已，这不是绑定的。kernel的出现要远远早于SVM，应用范围也远不止SVM

3）并不是所有情况下的kernel都要求满足Mercer条件（任何核矩阵为半正定的函数都可以作为核函数），SVM和GP（高斯过程）要求满足，但L1VM、L2VM、RVM都不要求kernel必须满足Mercer条件

4）Kernel是描述点和点之间关系的，或者说是距离。从距离空间出发，我们可以一步步往前走可以得到赋范向量空间，内积空间，然后是优美的希尔伯特空间。希尔伯特空间里面有好多概念，主要就是一个范数，一个内积。那什么是范数呢，范数就是我们之前强调的距离，或者说广义的距离。而什么又是内积呢？没错，内积就是这个距离的定义的方式。这就是为什么说由内积可以诱导出范数的原因了。既然kernel是用来描述点与点之间的关系或者说距离的话，那么一种可行的有效的方法就是用内积去刻画。

5）距离、内积（核函数）、相似度这三个词是等价的。(核函数会对应Gram矩阵)

6）Kernel 是隐式地将两个向量转换到其他形式然后求内积, 相比显式的转换可以极大的减少计算复杂度, 甚至可以将有限维的 x 转换到无限维. 与其先求出 $技术分享图片$ 再计算 $技术分享图片$ , 不如直接算 $技术分享图片$ , 这就是 kernel相对于手动(显式)转化的优势。