斐波那契数列 二进制数列

Posted 2020-11-19 zhibei

题目：写一个函数，输入n，求斐波那契数列的第n项。斐波那契数列的定义如下：

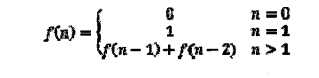
解题思路：

面试官期待的使用解法，我们可以把已经得到的数列中间项保存起来，如果下次需要计算的时候我们先查找一下，如果前面已经计算过就不用再重复计算了。

更简单的办法时从下往上计算，首先根据f(0)和f(1)算出f(2)，再根据f(1)和f(2)算出f(3)。。。以此类推就可以算出第n项了。

实现代码如下：

题目二：一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶共有多少种跳法。

解题思路：首先我们考虑最简单的情况。如果只有1级台阶，那显然只有一种跳法。如果有2级台阶，那就有两种跳的方法了：一种是分两次跳，每次跳1级；另外一种就是一次跳2级。

接着我们再来讨论一般的情况。我们把n级台阶时的跳法堪称是n的函数，记为f(n)。当n>2时，第一次跳的时候就有两种不同的选择：一是第一次只跳1级，此时跳法数目等于后面剩下的n-1级台阶的跳法数目，几位f(n-1);另外一种选择是第一次跳2级，此时跳法数目等于后面剩下的n-2级台阶的跳法数目，即为f(n-2).因此n级台阶的不同跳法的总数f(n)=f(n-1)+f(n+2).分析到这里，我们就不难看出这实际上就是斐波那契数列了。

 

题目三：二进制中1的个数

题目：请实现一个函数，输入一个整数，输出该数二进制表示中1的个数。例如把9表示成二进制是1001，有2为是1.因此如果输入9，该函数输出是2.

常规解法：为了避免死循环，我们可以不右移输入的数字i。首先把i和1做与运算，判断i的最低为是不是为1.接着把1左移一位得到2，再和i做与运算，就能判断i的次地位是不是1.。。。这样反复左移，每次都能判断i的其中一位是不是1.基于这种思路，我们可以把代码修改如下：

 

 能给面试官带来惊喜的解法：

我们把上面的分析总结起来就是：把一个整数减去1，再和原整数做与运算，会把该整数最右边一个1变成0.那么一个整数的二进制表示中有多少个1，就可以进行多少次这样的操作。基于这种思路，我们可以写出新的代码

 

相关题目：

用一条语句判断一个整数是不是2的整数次方。一个整数如果是2的整数次方，那么它的二进制表示中有且只有一位是1，而其他所有位都是0.根据前面的分析，把这个整数减去1之后再和它自己做与运算，这个整数中唯一的1就会变成0.

 

输入两个整数m和n，计算需要改变m的二进制表示中的多少位才能得到n。比如10的二进制表示为1010，13的二进制表示为1101，需要改变1010中的3位才能得到1101.我们可以分为两步解决这个问题：第一步求这两个数的异或，第二部统计异或结果中1的位数。

 

举一反三：

把一个整数减去1之后再和原来的整数做位与运算，得到的结果相当于是把整数的二进制表示中的最右边一个1变成0.很多二进制问题都可以用这个思路解决。