dpdk无锁队列rte_ring实现分析

Posted 2023-02-13 rayylee

1. 概述

rte_ring(以下简称ring)是一个高效率的无锁环形队列，它具有以下特点：

• FIFO
• 队列长度是固定的，所有指针存放在数组中
• 无锁实现(lockless)
• 多消费者或单消费者出队
• 多生产者或单消费者入队
• 批量(bulk)出队 - 出队N个对象，否则失败
• 批量(bulk)入队 - 入队N个对象，否则失败
• 突发(burst)出队 - 尽可能地出队N个对象
• 突发(burst)入队 - 尽可能地入队N个对象

与链表实现的队列相比，ring有以下优点：

• 更快 - 仅需要一次CAS(Compare-And-Swap)操作
• 比完全无锁的队列实现更简单
• 适配批量操作 - 由于指针存放在数组中，相比链表式队列多个对象的操作没有太大的cache miss

当然，ring也有缺点：

• 队列长度固定
• 比链表式队列更消耗内存(因为创建的时候队列长度便固定了)

ring的实现借鉴了 [freebsd_ring] 和 [linux_ringbuffer] 。每个ring都有唯一的名字。 用户不可能创建两个具有相同名称的ring（如果尝试调用rte_ring_create()这样做的话，将返回NULL）。

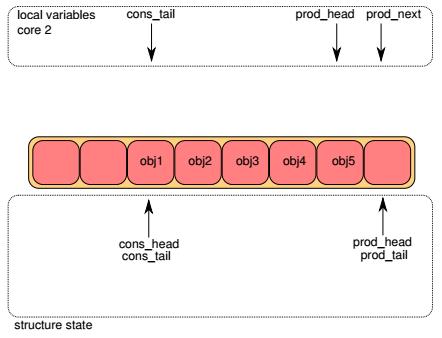
2. ret_ring无锁队列操作图解

下面将以多生产者(multi-producer, mp)的情形来说明ring入队时的操作，多消费者出队的基本原理可以此类比。

每个ring都有两对head，tail指针，一对用于生产者(入队)，另一对用于消费者(出队)。在下面各图中，上半部分表示lcore入队函数的局部变量， 下半部分表示ring的成员变量。objX表示队列中的对象。

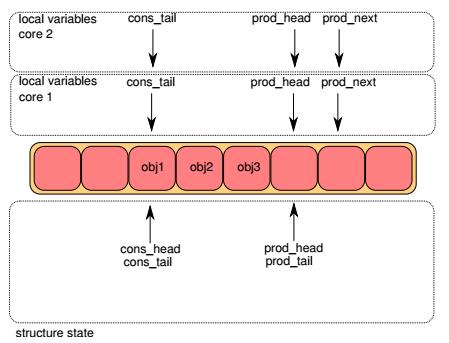
Step1

一开始，lcore1和lcore2局部变量pro_head和cons_tail都和queue成员一致，局部变量prod_next都指向队列插入位置，即prod_head的前面。

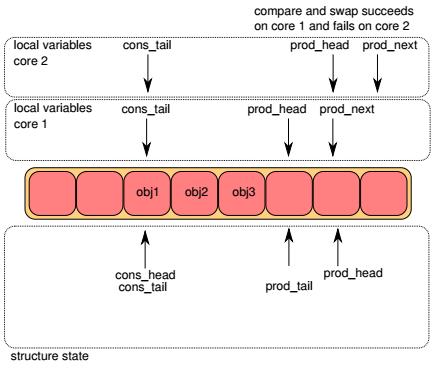
Step2

接下来两个lcore通过CAS指令进行竞争，更新ring->prod_head改为胜者lcore的prod_next：

• 如果ring->prod_head != prod_head, CAS失败，返回Step1
• 否则，CAS成功，ring->prod_head = prod_next

下图中，lcore1竞争获胜，而lcore2需要重新进行Step1：

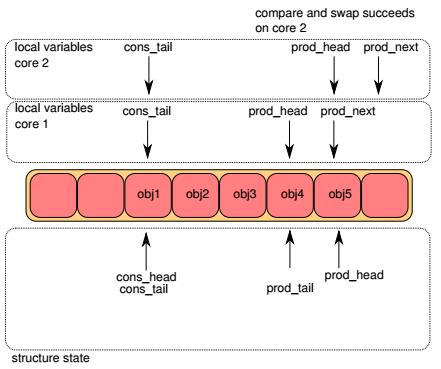
Step3

lcore2上的CAS操作也成功。lcore1将obj4入队，lcore2将obj5入队。

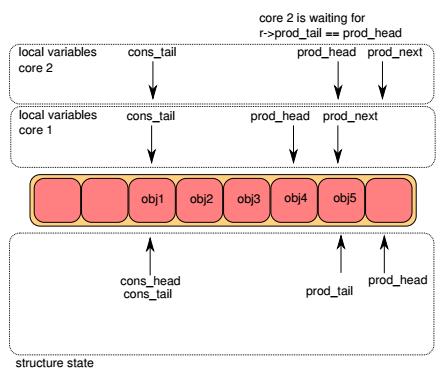
Step4

两个lcore进行竞争，更新ring->prod_tail：

• 如果ring->prod_tail != prod_head，CAS失败，继续尝试
• 否则，CAS成功, ring->prod_tail = prod_next

下图中，lcore1竞争获胜，lcore1上的入队操作到此结束。

Step5

lcore2如Step4一样，更新ring->prod_tail。至此lcore2的入队操作也已完成。

3. 代码分析

3.1 rte_ring 结构体：

1 struct rte_ring  2     char name[RTE_RING_NAMESIZE];    /**< Name of the ring. */  3     int flags;                       /**< Flags supplied at creation. */  4     const struct rte_memzone *memzone;  5             /**< Memzone, if any, containing the rte_ring */  6  7     struct prod  8         uint32_t watermark;      /**< Maximum items before EDQUOT. */  9         uint32_t sp_enqueue;     /**< True, if single producer. */ 10         uint32_t size;           /**< Size of ring. */ 11         uint32_t mask;           /**< Mask (size-1) of ring. */ 12         volatile uint32_t head;  /**< Producer head. */ 13         volatile uint32_t tail;  /**< Producer tail. */ 14     prod __rte_cache_aligned; 15 16     struct cons 17         uint32_t sc_dequeue;     /**< True, if single consumer. */ 18         uint32_t size;           /**< Size of the ring. */ 19         uint32_t mask;           /**< Mask (size-1) of ring. */ 20         volatile uint32_t head;  /**< Consumer head. */ 21         volatile uint32_t tail;  /**< Consumer tail. */ 22 #ifdef RTE_RING_SPLIT_PROD_CONS 23     cons __rte_cache_aligned; 24 #else 25     cons; 26 #endif 27 28 #ifdef RTE_LIBRTE_RING_DEBUG 29     struct rte_ring_debug_stats stats[RTE_MAX_LCORE]; 30 #endif 31 32     void * ring[0] __rte_cache_aligned; /**< Memory space of ring starts here. 33                                          * not volatile so need to be careful 34                                          * about compiler re-ordering */ 35 ;

3.2 入队函数 __rte_ring_mp_do_enqueue：

1 static inline int __attribute__((always_inline))  2 __rte_ring_mp_do_enqueue(struct rte_ring *r, void * const *obj_table,  3              unsigned n, enum rte_ring_queue_behavior behavior)  4  5     uint32_t prod_head, prod_next;  6     uint32_t cons_tail, free_entries;  7     const unsigned max = n;  8     int success;  9     unsigned i, rep = 0; 10     uint32_t mask = r->prod.mask; 11     int ret; 12 13     do 14         n = max; 15 16         prod_head = r->prod.head; 17         cons_tail = r->cons.tail; 18         free_entries = (mask + cons_tail - prod_head); 19 20         if (unlikely(n > free_entries)) 21             if (behavior == RTE_RING_QUEUE_FIXED) 22                 return -ENOBUFS; 23             24             else 25                 if (unlikely(free_entries == 0)) 26                     return 0; 27                 28 29                 n = free_entries; 30             31         32 33         prod_next = prod_head + n; 34         success = rte_atomic32_cmpset(&r->prod.head, prod_head, 35                           prod_next); 36     while (unlikely(success == 0)); 37 38     ENQUEUE_PTRS(); 39     rte_smp_wmb(); 40 41     if (unlikely(((mask + 1) - free_entries + n) > r->prod.watermark)) 42         ret = (behavior == RTE_RING_QUEUE_FIXED) ? -EDQUOT : 43                 (int)(n | RTE_RING_QUOT_EXCEED); 44     45     else 46         ret = (behavior == RTE_RING_QUEUE_FIXED) ? 0 : n; 47     48 49     while (unlikely(r->prod.tail != prod_head)) 50         rte_pause(); 51 52         if (RTE_RING_PAUSE_REP_COUNT && 53             ++rep == RTE_RING_PAUSE_REP_COUNT) 54             rep = 0; 55             sched_yield(); 56         57     58     r->prod.tail = prod_next; 59     return ret; 60

第34-36行处理多个producer的竞争，没有竞争到写入位置的线程将继续循环。

第39行插入了一个rte_smp_wmb()调用，对这个函数DPDK文档的解释是：

Write memory barrier between lcores. Guarantees that the STORE operations that precede the rte_smp_wmb() call are globally visible across the lcores before the the STORE operations that follows it.

第49行的循环用于无锁同步对prod.tail的修改。

ENQUEUE_PTRS宏函数：

1 #define ENQUEUE_PTRS() do \\  2     const uint32_t size = r->prod.size; \\  3     uint32_t idx = prod_head & mask; \\  4     if (likely(idx + n < size)) \\  5         for (i = 0; i < (n & ((~(unsigned)0x3))); i+=4, idx+=4) \\  6             r->ring[idx] = obj_table[i]; \\  7             r->ring[idx+1] = obj_table[i+1]; \\  8             r->ring[idx+2] = obj_table[i+2]; \\  9             r->ring[idx+3] = obj_table[i+3]; \\ 10          \\ 11         switch (n & 0x3) \\ 12             case 3: r->ring[idx++] = obj_table[i++]; \\ 13             case 2: r->ring[idx++] = obj_table[i++]; \\ 14             case 1: r->ring[idx++] = obj_table[i++]; \\ 15          \\ 16      else \\ 17         for (i = 0; idx < size; i++, idx++)\\ 18             r->ring[idx] = obj_table[i]; \\ 19         for (idx = 0; i < n; i++, idx++) \\ 20             r->ring[idx] = obj_table[i]; \\ 21      \\ 22 while(0)

第5行，如果n>4，则把它分成数次写入，每次写入4个指针；不足4的余数在switch语句中写入。

3.3 出队函数 __rte_ring_mc_do_dequeue ：

1 static inline int __attribute__((always_inline))  2 __rte_ring_mc_do_dequeue(struct rte_ring *r, void **obj_table,  3          unsigned n, enum rte_ring_queue_behavior behavior)  4  5     uint32_t cons_head, prod_tail;  6     uint32_t cons_next, entries;  7     const unsigned max = n;  8     int success;  9     unsigned i, rep = 0; 10     uint32_t mask = r->prod.mask; 11 12     do 13         n = max; 14 15         cons_head = r->cons.head; 16         prod_tail = r->prod.tail; 17         entries = (prod_tail - cons_head); 18 19         if (n > entries) 20             if (behavior == RTE_RING_QUEUE_FIXED) 21                 return -ENOENT; 22             23             else 24                 if (unlikely(entries == 0)) 25                     return 0; 26                 27 28                 n = entries; 29             30         31 32         cons_next = cons_head + n; 33         success = rte_atomic32_cmpset(&r->cons.head, cons_head, 34                           cons_next); 35     while (unlikely(success == 0)); 36 37     DEQUEUE_PTRS(); 38     rte_smp_rmb(); 39 40     while (unlikely(r->cons.tail != cons_head)) 41         rte_pause(); 42 43         if (RTE_RING_PAUSE_REP_COUNT && 44             ++rep == RTE_RING_PAUSE_REP_COUNT) 45             rep = 0; 46             sched_yield(); 47         48     49     r->cons.tail = cons_next; 50 51     return behavior == RTE_RING_QUEUE_FIXED ? 0 : n; 52

1 #define DEQUEUE_PTRS() do \\  2     uint32_t idx = cons_head & mask; \\  3     const uint32_t size = r->cons.size; \\  4     if (likely(idx + n < size)) \\  5         for (i = 0; i < (n & (~(unsigned)0x3)); i+=4, idx+=4) \\  6             obj_table[i] = r->ring[idx]; \\  7             obj_table[i+1] = r->ring[idx+1]; \\  8             obj_table[i+2] = r->ring[idx+2]; \\  9             obj_table[i+3] = r->ring[idx+3]; \\ 10          \\ 11         switch (n & 0x3) \\ 12             case 3: obj_table[i++] = r->ring[idx++]; \\ 13             case 2: obj_table[i++] = r->ring[idx++]; \\ 14             case 1: obj_table[i++] = r->ring[idx++]; \\ 15          \\ 16      else \\ 17         for (i = 0; idx < size; i++, idx++) \\ 18             obj_table[i] = r->ring[idx]; \\ 19         for (idx = 0; i < n; i++, idx++) \\ 20             obj_table[i] = r->ring[idx]; \\ 21      \\ 22 while (0)

3.4 32-bit取模索引

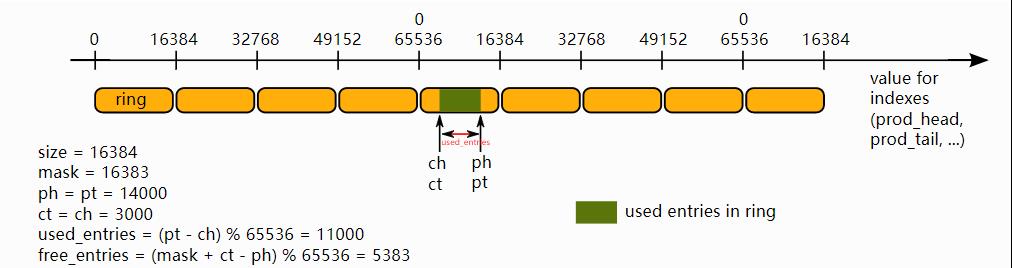
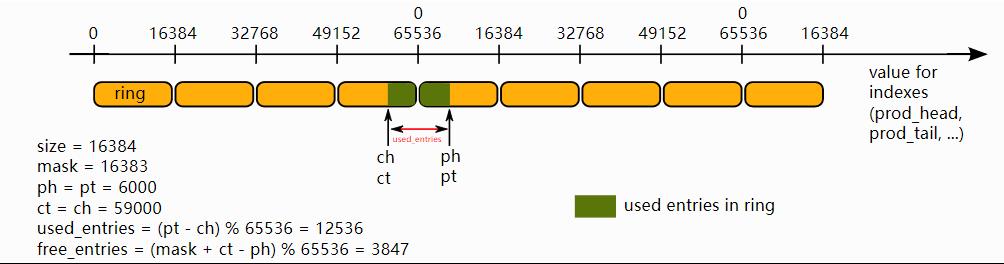
在前面介绍中，prod_head, prod_tail, cons_head 和 cons_tail索引由箭头表示。 但是，在实际实现中，这些值不会假定在0和 size(ring)-1 之间。 索引值在 0 ～ 2^32 -1之间，当我们访问ring本身时，我们屏蔽他们的值。 32bit模数也意味着如果溢出32bit的范围，对索引的操作将自动执行2^32 模。

下面解释索引值如何在ring中使用。为了简化说明，使用模16bit操作，而不是32bit。 另外，四个索引被定义为16bit无符号整数，与实际情况下的32bit无符号数相反。

这个ring包含11000对象。

这个ring包含12536个对象。

我们在上面的例子中使用模65536操作。 在实际执行情况中，这种低效操作是多余的，当溢出时会自动执行。代码始终保证生产者和消费者之间的距离在0 ～ size(ring)-1之间。 基于这个属性，我们可以对两个索引值做减法，而不用考虑溢出问题。任何情况下，ring中的对象和空闲对象都在 0 ～ size(ring)-1之间，即便第一个减法操作已经溢出：

uint32_t entries = (prod_tail - cons_head); uint32_t free_entries = (mask + cons_tail -prod_head);

参考文档

[dpdk_guide_ring]   DPDK programmer’s guide - Ring Library

[freebsd_ring]          FreeBSD buf_ring

[linux_ringbuffer]     Linux Lockless Ring Buffer

[lockfree_queue]     Yet another implementation of a lock-free circular array queue

[lockfree_coolshell] 酷壳：无锁队列的实现