各题型归纳总结
Posted 萌萌滴太阳
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了各题型归纳总结相关的知识,希望对你有一定的参考价值。
文章目录
二分
两种代码模板
代码1
- 代码1:在循环中查找元素
适合知道num[mid]等于什么,才能得到结果的情况
public class Solution
// 「力扣」第 704 题:二分查找
public int search(int[] nums, int target)
int len = nums.length;
int left = 0;
int right = len - 1;
// 目标元素可能存在在区间 [left, right]
//区间还剩一个元素时,继续循环
while (left <= right)
// 推荐的写法是 int mid = left + (right - left) / 2;
int mid = (left + right) / 2;
if (nums[mid] == target)
return mid;
else if (nums[mid] < target)
// 目标元素可能存在在区间 [mid + 1, right]
left = mid + 1;
else
// 目标元素可能存在在区间 [left, mid - 1]
right = mid - 1;
return -1;
代码2
- 代码2(1):在循环体中排除目标元素一定不存在的区间
适合 不知道num[mid]等于什么 才能得到结果,但知道什么情况下可以缩小区间,的情况。
使用 if (nums[mid] < target)判断;
public class Solution
// 「力扣」第 704 题:二分查找
public int search(int[] nums, int target)
int len = nums.length;
int left = 0;
int right = len - 1;
// 目标元素可能存在在区间 [left, right]
//区间还剩一个元素时,退出循环
while (left < right)
int mid = left + (right - left) / 2;
//这里注意使用nums[mid] < target;
//若使用nums[mid] > target,则mid需要上取整;
if (nums[mid] < target)
// 下一轮搜索区间是 [mid + 1, right]
left = mid + 1;
else
// 下一轮搜索区间是 [left, mid]
right = mid;
if (nums[left] == target)
return left;
return -1;
- 代码2(2):在循环体中排除目标元素一定不存在的区间
使用if (nums[mid] > target) 判断;会出现left = mid;mid需要上取整:int mid = left + (right - left + 1) / 2;防止死循环
即,出现left = mid情况,mid需向上取整int mid = left + (right - left + 1) / 2;防止死循环。
public class Solution
// 「力扣」第 704 题:二分查找
public int search(int[] nums, int target)
int len = nums.length;
int left = 0;
int right = len - 1;
while (left < right)
int mid = left + (right - left + 1) / 2;
if (nums[mid] > target)
// 下一轮搜索区间是 [left, mid - 1]
right = mid - 1;
else
// 下一轮搜索区间是 [mid, right]
left = mid;
if (nums[left] == target)
return left;
return -1;
思考
二分的思想是,通过num[mid]与一个target对比,来缩小区间,
- 当给定target时,自然与target比较;
- 当未给定target时,找那些和mid比较 能产生缩小区间效果的元素,如:
左右边界常作为target,
有重复元素的情况
针对有重复的情况,是将下面两种**无重复情况**下的划分:
nums[l] <= nums[mid]
nums[l] > nums[mid])
改为下面三种划分,将等于的情况单独提取出来,【适合重复情况】
nums[l] < nums[mid]
nums[l] == nums[mid] //若nums[l]不是目标值,因为相等,所以可以缩小一个范围,即l++;
nums[l] > nums[mid])
在有序数组中进行查找一个数(二分下标)
在整数范围内查找一个整数(二分答案)
山峰数组
arr[mid] 与 arr[mid + 1]比较
动态规划
找题目中的约束条件,然后根据约束条件定义状态
-
动态规划的用途:求解多阶段决策问题
动态规划解决的是这样一类问题:多阶段决策问题。这里的「阶段」就是生活语言:解决一个问题分很多步骤,每一个步骤又有很多种选择,这一点和「回溯算法」是一样的。
通常可以把多阶段决策问题画成一张树形图。 -
动态规划与回溯算法的区别
「动态规划」与「回溯算法」在问题问法上的区别是:「动态规划」问题通常只问结果,即只问最优值是多少,或者问解决方案的个数,而不问具体解(具体的解决方案)是什么;
「回溯算法」问题通常让我们给出一个问题的所有解决方案,要求我们返回的是一个嵌套列表。
能够使用动态规划解决的问题,一定可以使用回溯算法解决。但是我们要清楚一个事实:回溯算法的时间复杂度很高。在只问最优值是多少的场景下,没有必要记录每个阶段的每一个步骤。动态规划方法很多时候的意义在于评估算法的上限。
从题目中辨识是否用DP
重复子问题
剑指 Offer 46. 把数字翻译成字符串
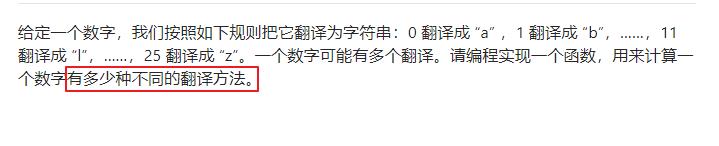
求:计算一个数字有多少种不同的翻译方法。
只是求有多少种,而不是求出每种的解决方案,即DP。【若求所有解决方案,则用回溯】
91. 解码方法
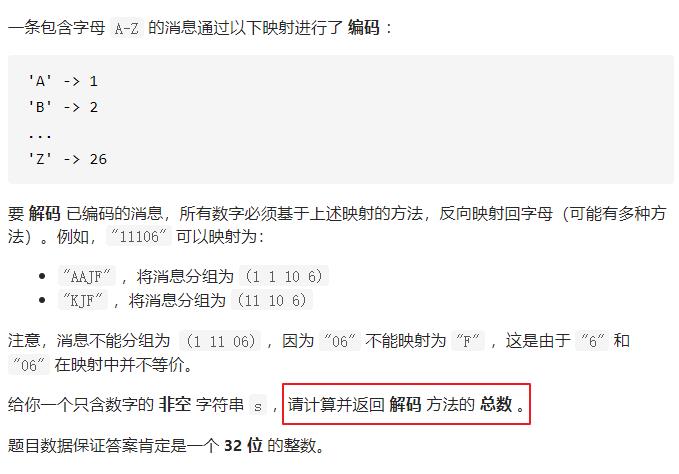
求:请计算并返回 解码 方法的 总数
只是求有多少种,而不是求出每种的解决方案,即DP。【若求所有解决方案,则用回溯】
最优子结构
它们的问法都一样:
求解一个问题的最优值是多少,但没有问最优值是怎么来的。以后遇到这样的问题,需要有一定敏感,可能这个问题考察的是动态规划(还有可能考察广度优先遍历、贪心算法)。
分析最优子结构的重要方法依然是:通过研究具体的例子,画图分析。
322. 零钱兑换

279. 完全平方数

343. 整数拆分

377. 组合总和 Ⅳ

对于 nums = [1,2,3], target = 4
dp[4] = dp[4 - 1] + dp[4 - 2] + dp[4 - 3]
即,
dp[target ] = dp[target - nums[0] ] + dp[target - nums[1] ] + dp[target - nums[2] ] + …【target - nums[2] >=0)】
class Solution
public int combinationSum4(int[] nums, int target)
int[] dp = new int[target + 1];
//dp[0]没实际意思,由dp[1] = 1 = dp[0]推出;
dp[0] = 1;
for(int j = 1 ; j <= target ; j++)
for(int i = 0 ; i < nums.length ; i++)
if(j >= nums[i]) dp[j] = dp[j] + dp[j - nums[i]];
return dp[target];
无后效性【多阶段、有约束 的决策最优化问题】

不同路径

- 只需求出路径个数,不需求出具体方案;
打家劫舍
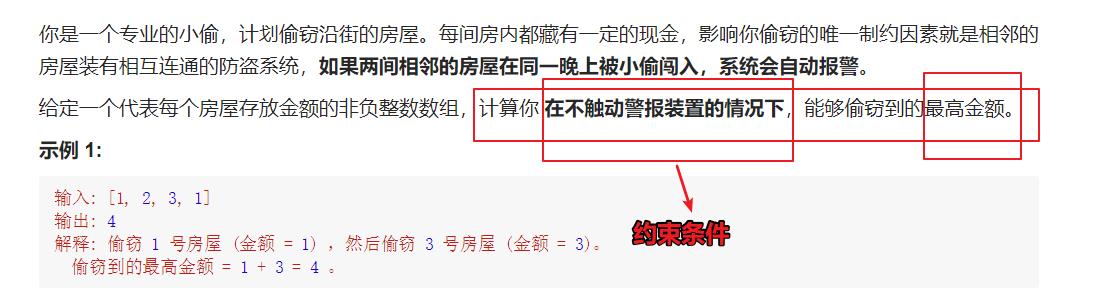
- 题目只问最优值,并没有问最优解,
因此可以考虑使用「动态规划」。 - 约束条件:在不触动警报装置的情况下,
即分一个房子偷或不偷两种情况;

贪心


以上是关于各题型归纳总结的主要内容,如果未能解决你的问题,请参考以下文章